Ex: théorème de Liouville

Auteurs: Stéphane Erard, Marc Fouchard

Auteur: Marc Fouchard

théorème de Liouville

Difficulté : ☆☆☆ Temps : 1h

Question 1)

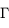Soit $\Gamma$ un volume de surface 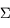$\Sigma$ . La variation du volume au cours du temps s'écrit:

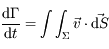$\frac{{\rm d} \Gamma}{{\rm d} t}=\int\int_{\Sigma} \vec{v} \cdot \vec{{\rm d}S}$ ,

où 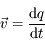$\vec{v}=\frac{{\rm d} q}{{\rm d} t}$ est le vecteur vitesse et 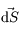$\vec{{\rm d}S}$ est un vecteur normal à la surface 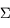$\Sigma$ et de norme égale à une élément de surface.

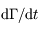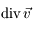Exprimer ${\rm d}\Gamma/{\rm d} t$ en vonction de la divergence de la vitesse ${\rm div}\, \vec{v}$ .

Solution

Question 2)

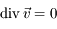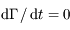Montrer que ${\rm div}\,\vec{v}=0$ et donc que ${\rm d}\Gamma \,/\, {\rm d}t=0$ .

Solution