

Ex: photométrie des surfaces planétaires |
Difficulté : ☆☆ Temps : 45 min
On assimile le Soleil à un corps noir. Quelle est la puissance rayonnée par un élément de surface dans une direction donnée ?
Calculer la luminance intégrale (intégrée spectralement), toujours dans une direction donnée. Application numérique.
Calculer la luminosité totale d'un élément de surface (rayonnée dans toutes les directions). Commenter.
Calculer la puissance totale émise par le Soleil. Application numérique (on donne pour le rayon du Soleil 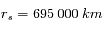 ).
).
Difficulté : ☆☆ Temps : 20 min
Le cas des surfaces planétaires est différent, leur capacité à réfléchir le rayonnement solaire dépendant de leur état physique : rugosité, taille des particules en surface... En outre la position du Soleil intervient également puisqu'on observe maintenant en réflexion (voir Figure 2). Le modèle lambertien est encore adapté aux surfaces très claires, mais ne décrit pas correctement les propriétés de la Lune ou des astéroïdes qui sont relativement sombres. On utilise souvent le modèle de Lommel-Seeliger, qui donne la luminance comme :
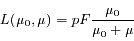
où p est l'albedo de la surface (coefficient de réflexion sous incidence et émergence nulles), F est le flux solaire à la distance de la planète, 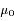 et
et 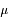 sont les cosinus des angles d'incidence et d'émergence.
sont les cosinus des angles d'incidence et d'émergence.
On utilise la réflectance hémisphérique pour étudier les propriétés thermiques des surfaces. Celle-ci est définie comme :
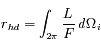
où 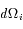 est l'angle solide élémentaire dans la direction d'incidence.
est l'angle solide élémentaire dans la direction d'incidence.
Calculer cette quantité en fonction des variables 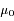 et
et 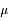 .
.