

Dans le problème des 2-corps |
Auteur: Alain Vienne
Quand on formule le problème des 2-corps, on arrive au problème de Képler, c'est-à-dire à l'équation différentielle vectorielle suivante:
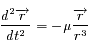
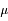 est une constante réelle positive et
est une constante réelle positive et 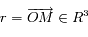 .
. 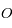 est un point fixe et on étudie le mouvement de
est un point fixe et on étudie le mouvement de 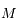 .
.
Les deux exercices proposés donnent la loi des aires et l'intégrale de Laplace.
En fait, le premier exercice aura 2 conséquences: la première est que le mouvement est plan et la deuxième que la loi du mouvement est la loi des aires proprement dite:
