 |  |  |  |  |  |
Ex: Distance Terre Lune |
, 
, 
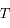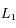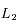et 
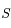sont respectivement les positions de la Terre, de la Lune pendant une éclipse de soleil, de la Lune pendant une éclipse de Lune, et du Soleil.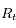 
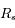et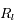 
sont les rayons terrestre, solaire et lunaire.
Calcul de la distance Terre-LuneDifficulté : ☆
Introduction
Il est connu que pendant une éclipse de Soleil, la Lune vient se placer entre la Terre et le Soleil et cache presque exactement le Soleil aux observateurs terrestres. Cela est possible car depuis la Terre, la Lune et le Soleil ont le même rayon apparent. Soit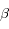 
le demi-angle sous lequel ces deux astres sont vus depuis la Terre (voir partie droite de la figure ci-dessous). Cet angle est connu directement par l'observation et vaut à peu près 0,25°.
Une éclipse de Lune se produit lorsque la Lune passe dans le cône d'ombre de la Terre éclairée par le Soleil (voir partie gauche de la figure ci-dessous). Soit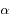 
l'angle d'ouverture de ce cône. Sa valeur est a priori inconnue. Aristarque de Samos avait observé que la largeur de ce cône au niveau de la Lune était de 3 diamètres lunaires.
Pour une question de lisibilité de la figure, la Lune n'a pas la même échelle sur la partie droite que sur la partie gauche. Les deux phénomène étant indépendants, cela n'a pas d'incidence sur le raisonnement.
 |  |
et 
en fonction de 
et 
.
en fonction de 
, 
et 
.
or 
. On a donc 
et 
et 
si on suppose le Soleil très grand devant la Terre ?
quand 
(défini sur la figure).
en fonction de 
et 
.
et 
sont alternes-internes et donc égaux.
. Par ailleurs, 
et 
d'après la question précédente.
et 
en fonction de 
.
et de hauteur 
est un rectangle.
et de hauteur 
. Le côté opposé à 
est de longueur 
d'après les observations d'Aristarque de Samos. Et d'après nos calculs précédents 
. En égalisant les deux hauteurs du rectangle on obtient donc 
.
et 