 Objetivos
Objetivos
Entender el funcionamiento de un espectrómetro de transformada de Fourier. Nos basaremos en las propiedades
de la TF relacionadas con las características deseadas del espectro.
Simulaciones
Una observación por espectrometría de Fourier requiere la elección de parámetros de Fourier
que permitan la grabación rápida del interferograma. La comparación entre el espectro inicial
y el espectro calculado basándose en un interferograma simulado permite hacerse una idea de
la calidad de las elecciones efectuadas.
Principio... y propiedades de la TF discreta
Un interferograma obtenido con pasos de diferencias de camino equidistantes de

tiene una frecuencia de corte de
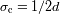
. El valor de esta frecuencia y con ello el de

tiene una gran importancia y por lo tanto no puede ser tomado al azar.
El espectro final es calculado por
transformada de Fourier rápida
basándose en el interferograma. Tal principio sólo es válido si los limites del
intervalo espectral libre
contienen la totalidad del
rango espectral
definido por el filtro de entrada. Nótese que los límites son múltiples enteros consecutivos
de
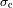
.
Intervalo espectral libre
Un
espectro distribuido sobre 2 intervalos
conduce también a un resultado incorrecto, aún cuando el tamaño del intervalo espectral libre sea
suficiente. Ello es debido al repliegue de las frecuencias durante la fft.
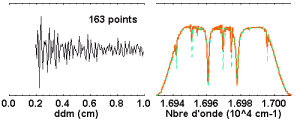
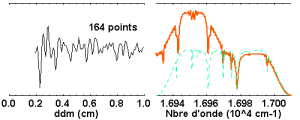
La cantidad de puntos del interferograma tiene que ser optimizada. Si es ligeramente diferente del valor
óptimo, el
muestreo incorrecto del señal
conduce a un espectro con aspecto deformado, a causa del repliegue indebido de frecuencias mal
separadas.
Resolución espectral
La resolución espectral varía en función de la
diferencia de camino
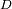
explorada. Ésta se describe simplemente como:
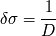
Ejemplo, para una línea a
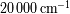
y
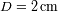
,
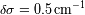
; el poder de resolución vale
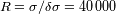
.
Sampling
El
sobremuestreo del interferograma
no sirve desde el momento en que la cantidad de puntos
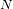
ha sido optimizada en el sentido de la transformada rápida de Fourier (FFT).

 tiene una frecuencia de corte de
tiene una frecuencia de corte de
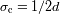 . El valor de esta frecuencia y con ello el de
. El valor de esta frecuencia y con ello el de
 tiene una gran importancia y por lo tanto no puede ser tomado al azar.
tiene una gran importancia y por lo tanto no puede ser tomado al azar.
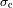 .
.
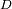 explorada. Ésta se describe simplemente como:
explorada. Ésta se describe simplemente como:
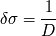
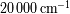 y
y
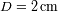 ,
,
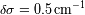 ; el poder de resolución vale
; el poder de resolución vale
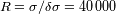 .
.
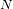 ha sido optimizada en el sentido de la transformada rápida de Fourier (FFT).
ha sido optimizada en el sentido de la transformada rápida de Fourier (FFT).