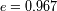La segunda ley de Kepler
La segunda ley de Kepler, o ley de las áreas, ilustrada en diversos casos.
Las diferentes "áreas barridas" por el radiovector en tiempos iguales son iguales. El sector angular
correspondiente es, por lo tanto, mucho mayor cerca del perihelio que del afelio. Este efecto
es bastante más significativo cuanto más se aproxime la excentricidad de la órbita a
1.
La segunda ley de Kepler permite la determinación de la ecuación horaria del movimiento a lo largo de
la trayectoria de un objeto.
Las posiciones de los objetos (
cometa Halley,
satélite en una órbita de transferencia a orbita geoestacionaria
) son representadas aquí en fechas equiespaciadas a lo largo de un periodo orbital. El movimiento es
menos uniforme cuanto más se aproxime a 1 la excentricidad de la órbita. La velocidad
orbital es mayor en el
periastro que en el
apoastro.
La tercera ley de Kepler
La tercera ley de Kepler implica un periodo más rápido cuanto más cercano a la estrella esté el planeta.
La
siguiente animación
muestra sus avances respectivos al cabo de un ciclo igual al periodo de revolución de Mercurio. Esta
animación supone (por las necesidades de la ilustración) que en un momento dado los planetas telúricos
podrían estar en fase.

La ley de Kepler en el sistema solar
Verificar con la ayuda de la
aplicación
la tercera ley de Kepler para los planetas del sistema solar.
- Seleccionar la primera casilla de la última columna.
- Escoger : =c1^2/b1^3
- ¿ Por qué en el sistema de unidades propuesto (distancia en UA, periodo en años), el
resultado es casi igual a 1 ?
Nótese que la validez del cálculo es peor para los planetas más allá de Júpiter que sienten un
campo de fuerza medio de masa total igual a la masa del Sol completada por la de
Júpiter.

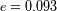
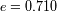 )
correspondiente a un perigeo a baja altitud y un apogeo a la altitud de una órbita geoestacionaria.
)
correspondiente a un perigeo a baja altitud y un apogeo a la altitud de una órbita geoestacionaria.