 Ejercicio 'Límite de Roche'
Ejercicio 'Límite de Roche'
Nivel ***
Tiempo necesario :
45 min
2)
Enunciar las fuerzas de interacción gravitacional
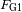
y
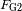
ejercidas por el astro masivo sobre
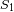
y
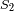
.
ayuda
solución
3)
El estudio del movimiento en el referencial giratorio introduce una aceleración de frenado. Determinarla
y expresar el término de inercia que va a sumarse en el balance de fuerzas expresado en el referencial
giratorio. Para simplificar los cálculos se considera que el baricantro del sistema planeta-satélite es el
mismo que le baricentro del planeta.
ayuda
solución
4)
Se denotan como
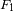
y
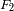
a las contribuciones totales (gravitacional e inercial) sobre
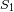
y
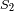
. Dar el nombre de la fuerza
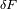
definida como la diferencia de
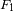
y
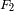
? y calcularla.
ayuda
solución
5)
Calcular la fuerza de cohesión
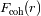
entre
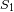
y
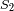
. Previamente, estimar su origen.
ayuda
solución
6)
Determinar el límite de Roche
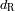
, distancia a la cual los términos de cohesión y de marea se equilibran. Expresarlo en función
de
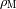
y de
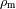
, las masas volúmicas respectivas del planeta y el satélite.
ayuda
solución
7)
Calcular el límite de Roche para el caso del sistema
Tierra-Luna.
Comparar el límite de Roche de la Tierra con la distancia Tierra-Luna.
solución
8)
Responder a la misma pregunta para Saturno y su satélite
Mimas,
suponiendo que el satélite, en formación entre sus anillos, tiene una masa volúmica idéntica a la de
Saturno. Calcular el límite de Roche en ese caso. Compararlo al radio de los anillos y al radio de los
satélites de Saturno.
solución
9)
Responder a la misma pregunta para el
Sol
visitado por un cometa en su perihelio. Comparar con el
perihelio del cometa Halley
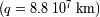
(supondremos que la expresión de la aceleración de frenado encontrado en el caso de una órbita
circular mantiene un orden de magnitud apropiado, incluso si no se puede aplicar a
priori).
solución

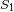 y
y
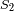 ) de radio
) de radio
 mantenidas unidas a partir de una interacción gravitacional. Se denota esta fuerza de cohesión
como
mantenidas unidas a partir de una interacción gravitacional. Se denota esta fuerza de cohesión
como
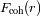 .
.

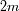 puede ser simulado como dos esferas de masa
puede ser simulado como dos esferas de masa
 y radio
y radio
 . Este satélite orbita alrededor de un planeta de masa
. Este satélite orbita alrededor de un planeta de masa
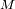 (
(
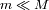 ), y radio
), y radio
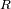 . La distancia entre los centros de masa del planeta y el satélite es
. La distancia entre los centros de masa del planeta y el satélite es
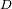 , con
, con
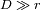 .
.
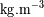 )
)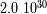
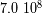
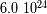
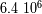
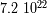
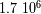
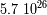
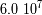
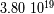
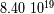
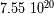
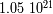
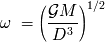
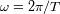 la pulsación del movimiento.
ayuda
ayuda
solución
la pulsación del movimiento.
ayuda
ayuda
solución
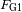 y
y
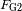 ejercidas por el astro masivo sobre
ejercidas por el astro masivo sobre
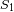 y
y
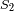 .
ayuda
solución
.
ayuda
solución
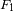 y
y
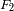 a las contribuciones totales (gravitacional e inercial) sobre
a las contribuciones totales (gravitacional e inercial) sobre
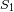 y
y
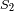 . Dar el nombre de la fuerza
. Dar el nombre de la fuerza
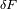 definida como la diferencia de
definida como la diferencia de
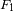 y
y
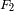 ? y calcularla.
ayuda
solución
? y calcularla.
ayuda
solución
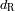 , distancia a la cual los términos de cohesión y de marea se equilibran. Expresarlo en función
de
, distancia a la cual los términos de cohesión y de marea se equilibran. Expresarlo en función
de
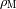 y de
y de
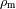 , las masas volúmicas respectivas del planeta y el satélite.
ayuda
solución
, las masas volúmicas respectivas del planeta y el satélite.
ayuda
solución
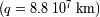 (supondremos que la expresión de la aceleración de frenado encontrado en el caso de una órbita
circular mantiene un orden de magnitud apropiado, incluso si no se puede aplicar a
priori).
solución
(supondremos que la expresión de la aceleración de frenado encontrado en el caso de una órbita
circular mantiene un orden de magnitud apropiado, incluso si no se puede aplicar a
priori).
solución