L'instrumentation astrophysique conduit souvent à des observations à la pointe de ce qui est faisable. Les signaux, obtenus après des heures d'observations chèrement acquises, doivent exprimer toute leur substantifique moelle. Une étape très importante est donc l'analyse du signal.
Cette section expose diverses pistes pour :
- Comprendre l'allure d'un signal.
- Extraire le signal du bruit.
- Analyser le signal.
Quelques-unes des sources de bruit physique sont répertoriées à la page
bruits de détection.
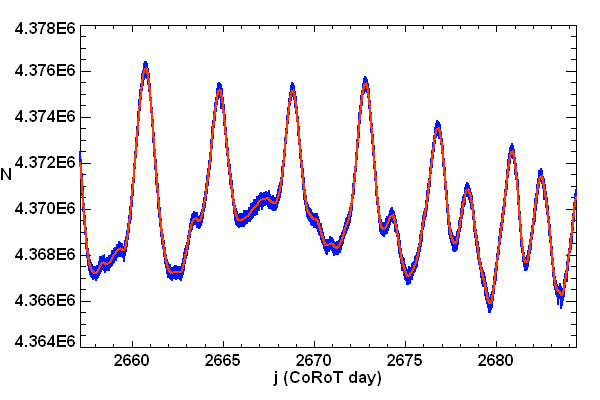
Exemple de filtrage. Série temporelle du flux de l'étoile HD 175726 observée par le photomètre à bord du satellite CoRoT, exprimé en nombre de photons, et série filtrée des hautes fréquences.
Crédit :
CNES/ASM
Détection et rapport signal à bruit
La détection d'un phénomène, comme par exemple une raie spectrale, nécessite de pouvoir distinguer le signal par rapport à ce qui n'est pas du signal, appelé bruit s'il présente un caractère aléatoire. On exprime ceci par un rapport, le rapport signal à bruit, d'autant plus important que le signal est fort par rapport au bruit.
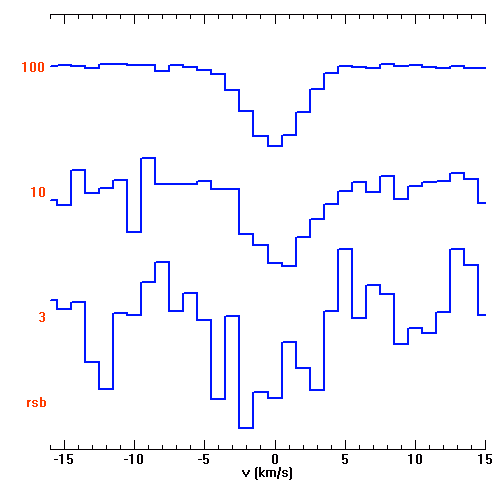
Allure d'une raie en absorption, observée à différents rapports signal à bruit.
La détection commence à être possible avec un rapport signal à bruit supérieur à 5. L'échelle spectrale est donnée en vitesse (km/s), centrée sur la raie.
Crédit :
ASM
Biais
Il ne faut pas confondre un signal parasite, ou biais observationnel, avec un bruit. Le biais qui affecte le signal possède des propriétés qui le distinguent tout à fait d'un bruit.
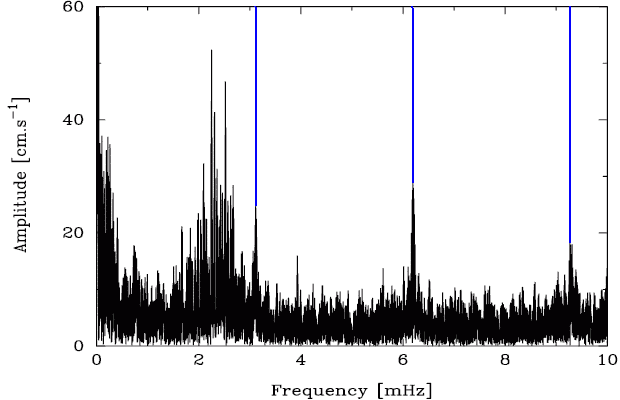
Exemple de biais. Un défaut dans le système de pointage du télescope est mis en évidence sur une cible atypique (alpha du Centaure, extrêmement brillant). Il s'ensuit une signature spectrale parasite à 3.1 mHz et à ses harmoniques.
Crédit :
ESO
Un biais très commun est un offset, càd un décalage du signal dû au fait que le niveau zéro du signal physique et le niveau zéro de sa traduction en signal électrique ne coïncident pas.
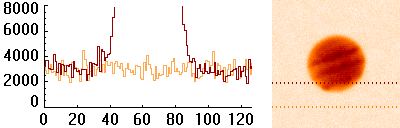
Exemple d'offset, sur une image simulée de Jupiter dans l'infrarouge thermique.
Les courbes orange et rouge sont des coupes de l'image ; elles représentent le flux (unité arbitraire) en fonction du numéro de pixel. Le fond de ciel, qui devrait être à zéro, ne l'est pas.
Crédit :
ASM
Bruits et signaux
L'astronomie regorge d'exemple de bruits devenus des signaux célèbres à partir du moment où leurs caractéristiques ont été identifiées.
- Le bruit remarqué par les radioastronomes dans toutes les directions d'observations, a été identifié par Penzias et Wilson en 1965 comme étant le rayonnement à 3 K du fond cosmologique
- Le bruit des observations de la photosphère solaire dans les années 1970 s'est révélé un signal acoustique très régulier, signature des modes d'oscillation du soleil. Aujourd'hui, plus de 10 millions de modes d'oscillations ont été identifiés, si bien que l'on connaît très précisément l'intérieur du Soleil.
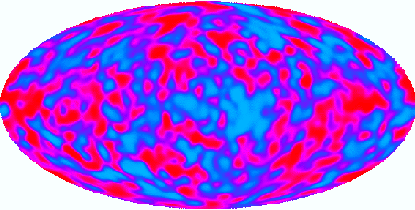
La carte du rayonnement du fond cosmologique, observée par le satellite Cobe, représentée en
coordonnées galactiques. Les couleurs codent les fluctuations par rapport à la température moyenne 2.728 K
Crédit :
NASA
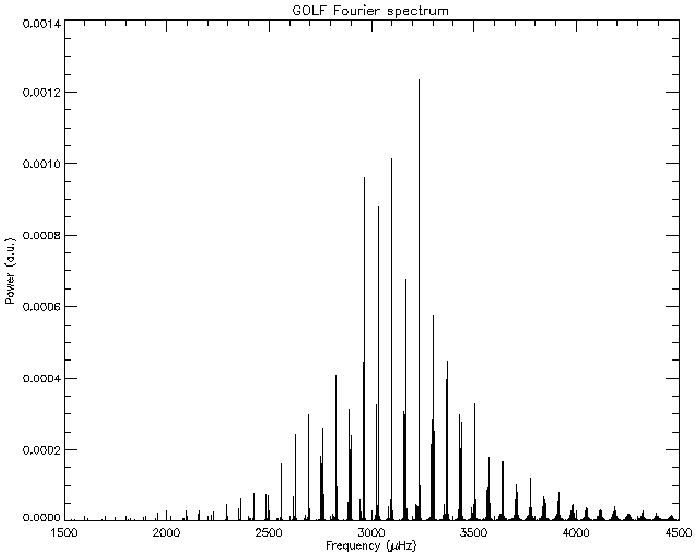
Spectre des modes d'oscillations du Soleil, avec des périodes voisines de 5 minutes. Observation de l'instrument Golf à bord de Soho.
Crédit :
SOHO
 Objectifs
Objectifs
Distinguer signaux et bruits.
Qualitativement
Le bruit de la circulation qui vous empêche d'entendre ce que dit votre ami(e) dans la rue, c'est du bruit... et ce que vous dit votre ami(e) a priori du signal. Mais une voiture qui accélère, est-ce vraiment un bruit, ou un signal parasite ?
Par analogie, la lumière du ciel diurne qui empêche de voir les étoiles de jour est-elle un bruit, un signal parasite ?
Signal, bruit
Tout observation va comporter, en plus du signal, des perturbations à ce signal.
Ces dernières résultent principalement de deux causes, intrinsèques et extrinsèques :
- Intrinsèquement, la nature même de la physique du signal implique l'existence de fluctuations (voir p.ex. comment l'arrivée des photons construit le bruit de Poisson).
- Par ailleurs, les conditions d'observation superposent au signal diverses autres contributions : signaux parasites, biais ou bruits.
Exemple de biais : le niveau de biais d'une image numérique prise avec une caméra CCD peut provenir du signal généré par la tension d'alimentation appliquée au détecteur.
Les propriétés d'un bruit
 Définition
Définition
Un bruit est un phénomène aléatoire.
On découvre par la suite deux types de bruit plus spécialement importants, obéissant à des statistiques poissonniennes ou gaussiennes.
Exemples
La distinction entre bruit et signal parasite est parfois complexe.
On peut prendre l'exemple du courant d'obscurité d'un détecteur, qui se superpose au flux observé.
Sa valeur moyenne est parfaitement quantifiable (tant de photoélectrons par pixel et par seconde), ce qui montre qu'il s'agit là d'un signal, parasite certes mais avec les propriétés d'un signal.
La vraie composante de bruit concerne les fluctuations de ce courant d'obscurité.
Identification d'un offset
A l'aide de l'appliquette, estimer l'offset affectant cette image de Jupiter dans l'infrarouge thermique.

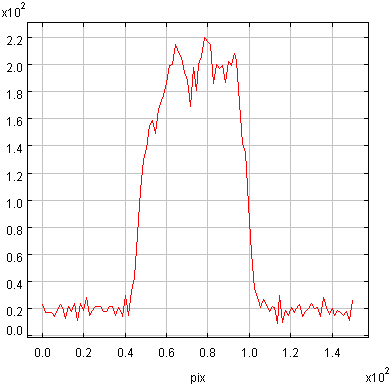
Une coupe montre un niveau d'offset aux alentours de 18 à 20, pour un signal planétaire 10 fois plus important.
Crédit :
ASM
Solution
Réalisations
Une loi de probabilité est déterministe. Mais ses réalisations sont ... aléatoires. C'est seulement avec un nombre élevé de réalisations que l'ensemble de ces réalisations retrace fidèlement la loi de probabilité. Si le nombre de réalisations est petit, on n'observe rien d'identifiable.
Loi uniforme, tirage d'un dé.
Crédit :
ASM
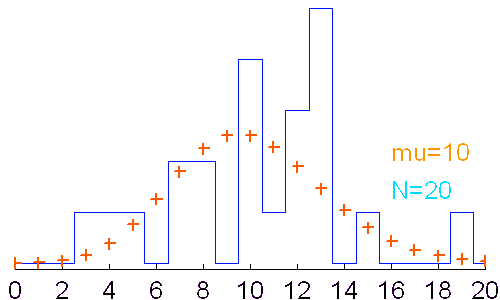
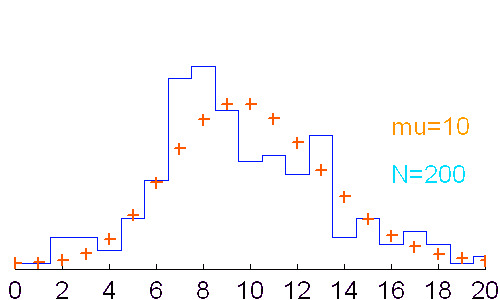
Réalisations d'un phénomène aléatoire obéissant à la loi de Poisson (moyenne = 10). Avec un nombre N de tirages peu élevé, la distribution des valeurs (courbe en bleu) ne ressemble que de très loin à la fonction de probabilité attendue (croix en rouge).
Crédit :
ASM
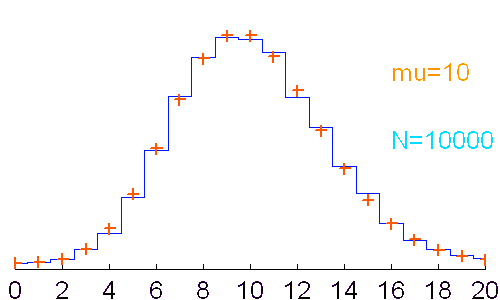
Réalisations d'un phénomène aléatoire obéissant à la loi de Poisson. Avec un nombre de tirages élevé, la distribution des valeurs trace convenablement la fonction de probabilité.
Crédit :
ASM
Estimations
Estimation de la moyenne et de l'écart type d'une loi. La moyenne peut être estimée de diverses façons, et la meilleure façon d'estimer une moyenne dépend de la loi de probabilité.
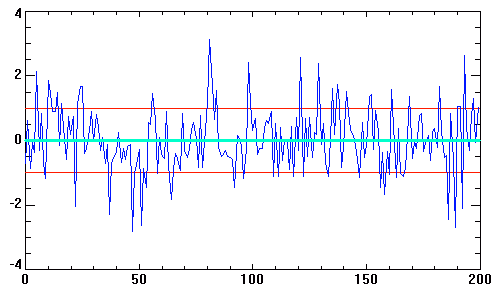
Moyenne (trait bleu ciel) et écart-type (droites de part et d'autre de la moyenne) pour un bruit blanc.
Crédit :
ASM
 Prérequis
Prérequis
Notions élémentaires de statistiques
 Objectifs
Objectifs
La définition d'un bruit repose sur ses propriétés statistiques. Cette page rappelle des notions simples de statistiques, en distinguant les lois de probabilité, leurs réalisations, et l'estimation de paramètres statistiques.
Loi de probabilité
La loi de probabilité d'une variable aléatoire 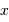 va être donnée par
va être donnée par 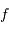 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 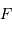 sa fonction de répartition
sa fonction de répartition 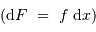 .
.
Parmi les moments centrés associés,
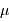 la moyenne et
la moyenne et 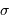 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
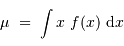
et :
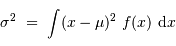
(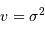 est la variance).
est la variance).
Une loi statistique possède des propriétés particulières, qui caractérisent tel ou tel phénomène : une loi poissonnienne (discrète) rend compte de l'arrivée d'événements indépendants, une loi gaussienne est souvent issue de l'addition d'un grand nombre de phénomènes indépendants...
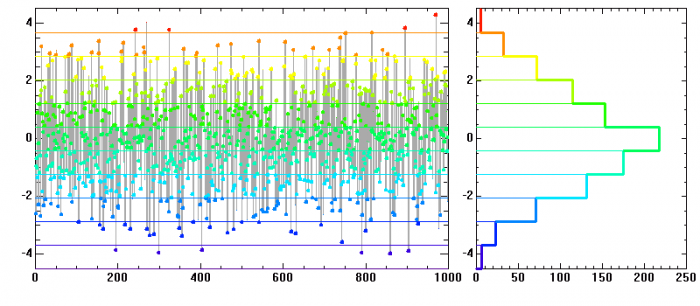
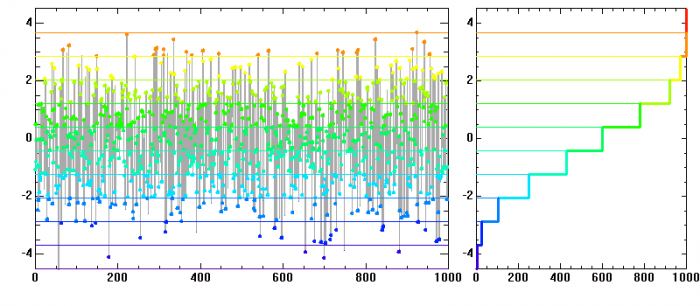
Réalisation d'une loi normale. L'histogramme se rapproche de la loi de probabilité.
Crédit :
ASM
Réalisations
La réalisation d'une loi de probabilité est aléatoire : un tirage de dés, réalisé 6 fois, ne conduira pas nécessaire à l'obtention une fois et une seule de chaque chiffre de 1 à 6. Plus le nombre de réalisations est grand, meilleur est l'accord entre l'observation de ces réalisations et la loi de probabilité.
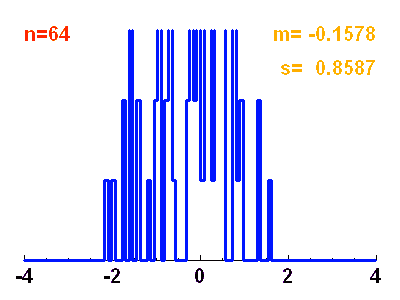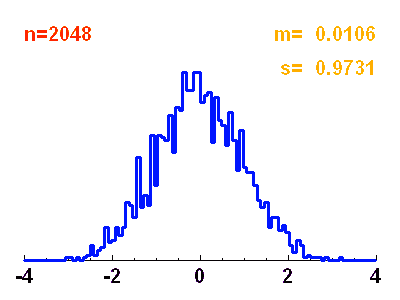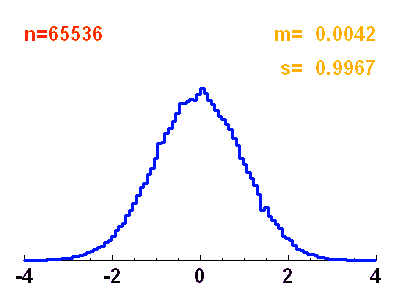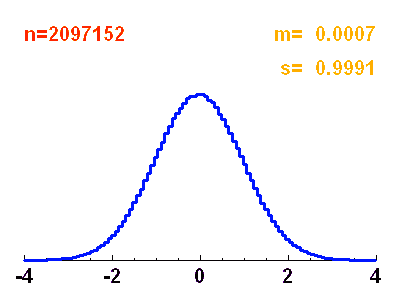
Histogramme d'une distribution de
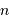
points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.
Crédit :
ASM
Loi statistique et réalisation
L'animation ci-joint montre comment est réalisée en pratique une distribution normale. Ce n'est qu'avec un très grand nombre de tirages que l'histogramme des réalisations ressemble vraiment à la distribution statistique.


Mesure de bruits
Les appliquettes ci-jointes dévoilent des signaux temporels bruités, affectés ou non d'une lente dérive. On se propose d'en mesurer le bruit et le
rapport signal à bruit.
Se servir des appliquettes pour :
- Déterminer la moyenne du signal.
- Le cas échéant, corriger de la dérive.
- Mesurer l'écart-type, en appliquant sa définition et la fonction ajustement.
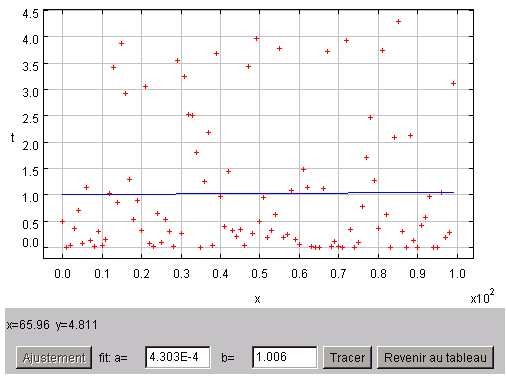
Avec l'appliquette, on calcule
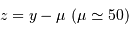
et puis
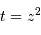
. L'ajustement donne un écart-type de 1.
Crédit :
ASM
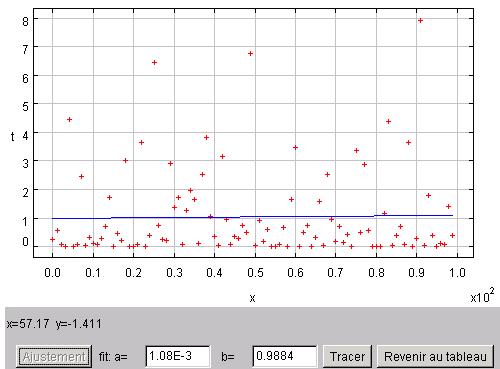
On remarque que la distribution des valeurs de
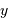
n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0
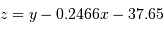
et puis
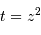
. L'ajustement donne un écart-type de 1.04.
Crédit :
ASM
Rapport signal à bruit
Le rapport signal à bruit conditionne toute observation. S'il est faible, on ne voit que du ... bruit.

Allure d'une raie en absorption, observée à différents rapports signal à bruit.
L'identification de la raies peut être possible avec un rapport signal à bruit supérieur à 3.
Crédit :
ASM
Détection et rapport signal à bruit
La détection d'un phénomène, comme par exemple une raie spectrale, nécessite un rapport signal à bruit typiquement supérieur à 3.
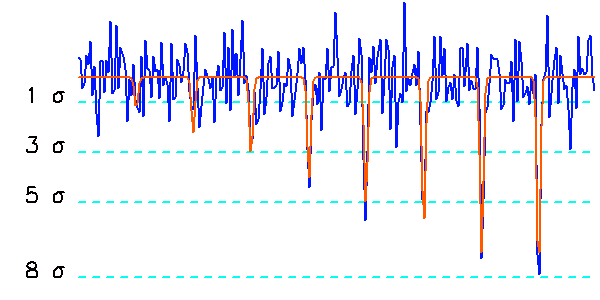
Simulation d'une portion de spectre en absorption, à rapport signal de bruit de 5 et 10.
Un motif avec un rapport signal à bruit supérieur à 3 peut très bien être du bruit, et ne peut donc être identifié à quelque signal que ce soit.
Si le bruit est strictement gaussien, on admet qu'une détection est certaine dès lors qu'elle sort de plus de 5 fois du niveau de bruit.
Crédit :
ASM
 Prérequis
Prérequis
Notions de probabilités et statistiques
Définition
On définit le rapport signal à bruit d'un signal comme le rapport des énergies du signal et du bruit. L'énergie du signal est représentée par sa valeur moyenne 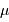 , et celle du bruit par l'écart-type
, et celle du bruit par l'écart-type 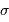 . Le rapport signal à bruit est donc :
. Le rapport signal à bruit est donc :
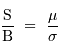
Si le signal est affecté d'un biais systématique 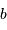 , il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
, il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
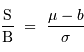
La composante de biais peut être p.ex., pour un signal évoluant dans le temps, un signal parasite apparaissant à plus basse fréquence.
Addition des bruits
Si les différents bruits contribuant à un signal sont indépendants les uns des autres, leurs
écarts-types s'ajoutent quadratiquement pour construire l'écart-type total :
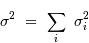
Il s'ensuit le rapport signal à bruit :
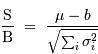
Détection et rapport signal à bruit
Identifier un spectre est d'autant plus aisé que le rapport signal à bruit est bon. En pratique, une raie a priori inconnue devient détectable pour un rapport signal à bruit supérieur à 5.
Spectre stellaire bruité
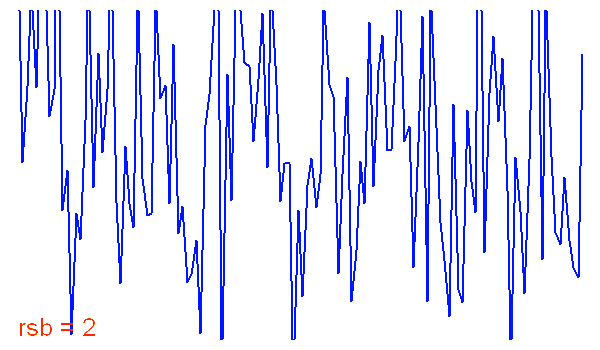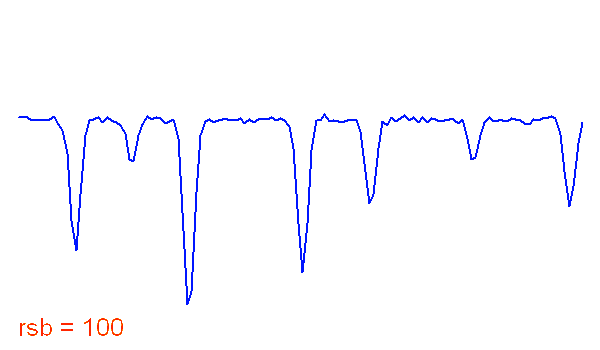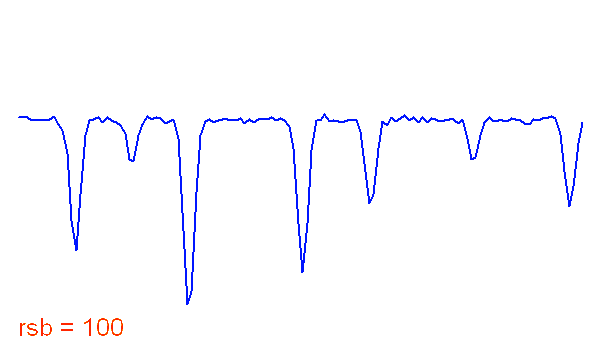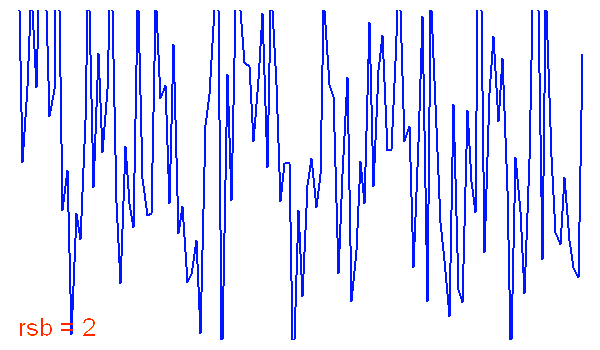
Allure d'une portion de spectre stellaire, en fonction du rapport signal à bruit.
Crédit :
ASM
Evolution temporelle du rapport signal à bruit
Si le bruit est dominé par le bruit de photons, le rapport signal à bruit augmente avec la durée d'observation, comme le montre cette
simulation.
Observation bruitée

La galaxie M31, imagée à différents niveaux de bruit.
Crédit :
ASM
 Bruit dominant
Bruit dominant
Difficulté : ☆☆
Temps : 30 min
On recueille le signal d'une cible stellaire. Le rapport signal à bruit s'écrit :
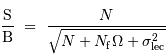
avec 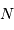 le nombre de photoélectrons reçus,
le nombre de photoélectrons reçus, 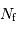 relié à un signal de fond,
relié à un signal de fond, 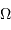 la taille angulaire de la cible, et
la taille angulaire de la cible, et 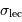 le bruit de lecture
le bruit de lecture
Question 1)
Identifier précisément les différents termes de bruit contribuant au rapport signal à bruit, en précisant leur écart-type.
Au numérateur, on a tout simplement le signal, au dénominateur les bruits.
Il reste à identifier le terme 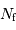 et à interpréter la somme du dénominateur.
et à interpréter la somme du dénominateur.
Question 2)
Simplifier l'expression du rapport signal à bruit pour le cas d'un objet très brillant, puis pour un objet très peu lumineux. Identifier l'exposant qui caractérise la dépendance en  du rapport signal à bruit.
du rapport signal à bruit.
Déterminer l'importance relative des différents bruits.
Question 3)
Déterminer comment le rapport signal à bruit varie avec le diamètre 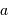 du collecteur ou le temps de pose
du collecteur ou le temps de pose 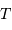 .
.
Comment le nombre de photoélectrons collectés varie-t-il avec le diamètre du collecteur ou le temps de pose ?
Conséquence du théorème de la limite centrale
La superposition de plusieurs variables aléatoires indépendantes les unes des autres conduit à une loi normale. C'est l'une des conséquences du théorème de la limite centrale. L'animation ci-jointe en montre un exemple.
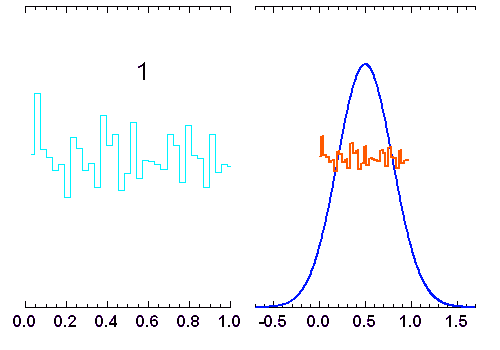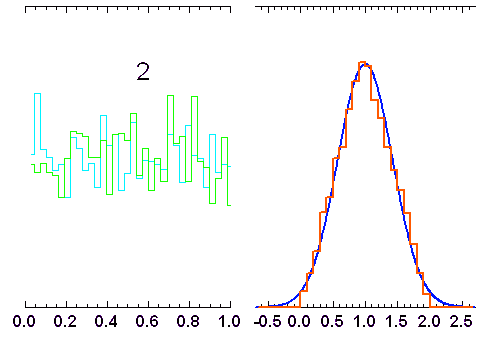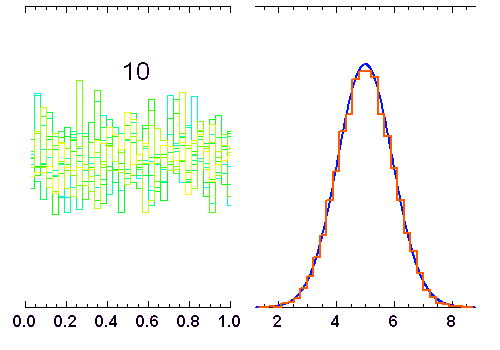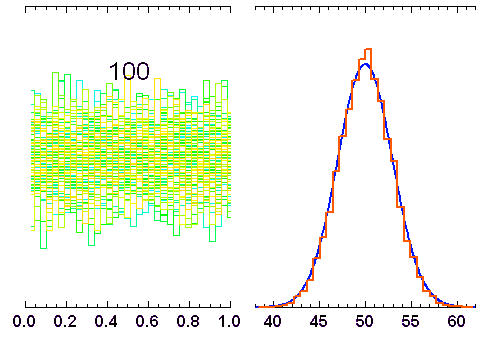
Addition de
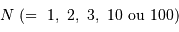
variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque
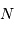
augmente, la distribution tend vers une loi gaussienne de moyenne
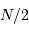
et écart type
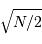
(courbe rouge). Pour
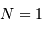
, la distribution reste bien sûr uniforme,
pour
elle garde une allure triangulaire.
Crédit :
ASM
Distribution gaussienne
Exemples de distributions gaussiennes.
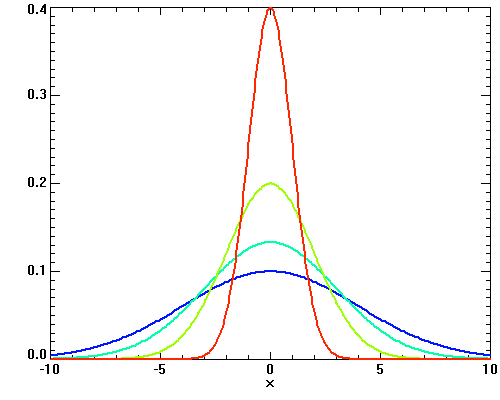
Distributions de Gauss. Moyennes toutes nulles et écarts-types de 1 à 4.
Crédit :
ASM
Bruit gaussien
Si un bruit est gaussien, la probabilité qu'il s'écarte de plus ou moins 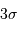 de la valeur moyenne est très faible. Cette propriété est mise à profit pour identifier le signal du bruit, mais ne marche que si le bruit est vraiment gaussien.
de la valeur moyenne est très faible. Cette propriété est mise à profit pour identifier le signal du bruit, mais ne marche que si le bruit est vraiment gaussien.
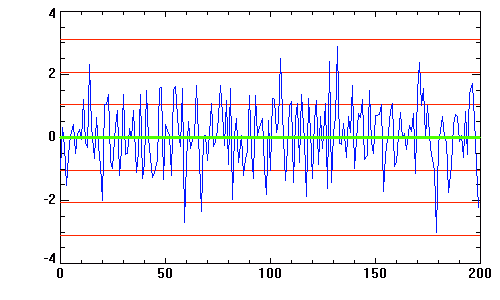
Bruit gaussien de moyenne nulle et d'écart-type 1. Peu de valeurs s'écartent de plus que
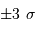
de la moyenne.
Crédit :
ASM
 Prérequis
Prérequis
Loi de probabilité ; éléments de statistique
Définition
Le théorème de la limite central implique qu'un bruit résultant de l'action indépendante de différents facteurs physiquesobéit à la loi de probabilité, dite loi normale :
![f(x) \ = \ {1\over \sqrt{2\pi}\sigma}\ \exp \left[ -{(x-\mu)^2\over 2 \sigma^2} \right]](../pages_analyser/equations_bruit-gaussien/equation9.png)
avec 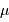 la moyenne et
la moyenne et 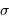 l'écart-type. Un tel bruit est dit gaussien.
l'écart-type. Un tel bruit est dit gaussien.
Détection d'un signal ?
De ce qui précède, peut-on dire qu'un événement qui s'écarte de plus de 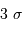 de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
On considère une détection sûre lorsqu'elle dépasse un seuil de 4 ou 5 fois l'écart-type. Mais, la difficulté réside souvent dans le fait que la nature d'un bruit n'est pas exactement gaussienne, ou que des signaux parasites non identifiés compliquent l'interprétation d'un signal.
Analyse en fréquence d'un bruit gaussien
L'analyse fréquentielle d'un bruit gaussien ne montre aucune composante privilégiée. Pour cette raison, on parle d'un bruit blanc.
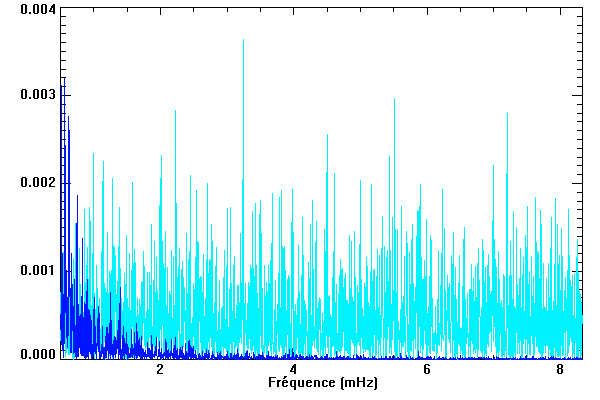
Les spectres de puissance de différents types de bruits : bruit instrumental en bleu foncé, bruit gaussienn en bleu clair. Le spectre du bruit gaussien ne présente pas de fréquence privilégiée, contrairement au bruit instrumental.
Crédit :
ASM

Marche au hasard à partir d'un point fixe. Le cercle mesure l'évolution moyenne, qui varie comme la racine carrée du nombre de pas effectués.
La couleur code l'évolution temporelle.
Crédit :
ASM
Marche au hasard
L'ivrogne et son lampadaire sont des acolytes précieux du physicien statisticien. L'ivrogne est supposé partir du lampadaire et accomplir un certain nombre de pas par unité de temps, mais dans n'importe quelle direction.
Au bout de 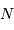 pas, il se sera éloigné du lampadaire d'une distance moyenne de
pas, il se sera éloigné du lampadaire d'une distance moyenne de 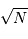 .
.

Identification d'un niveau de bruit
A l'aide de l'appliquette, estimer le niveau de bruit affectant cette image de Jupiter dans l'infrarouge thermique. L'exprimer en fonction du niveau maximal du signal (conseil : faire une coupe non sur la planète mais sur le fond de ciel).
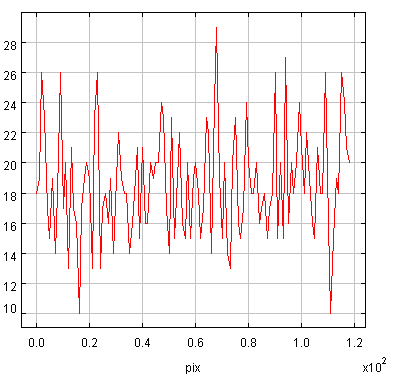
Une coupe sur le ciel seul montre un niveau d'offset aux alentours de 18 à 20, et un niveau de bruit entre 10 et 26. En supposant que le bruit est gaussien, on voit ses variations essentiellement à
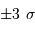
. On en déduit un niveau de bruit de l'ordre de 16/6=2.7. Le signal moyen étant d'environ 200, le rapport signal à bruit est voisin de 75.
Crédit :
ASM
Solution
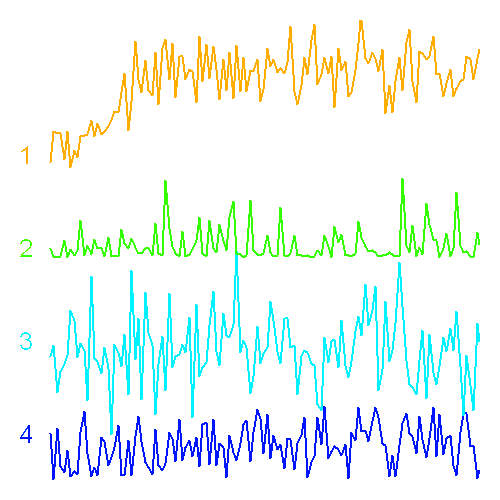
Quatre signaux : bruits gaussiens ou non ?
Crédit :
ASM
Statistique de Poisson
Lorsqu'une moyenne de 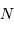 quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de
quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de 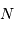 . La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus
. La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus  est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
Distribution de Poisson
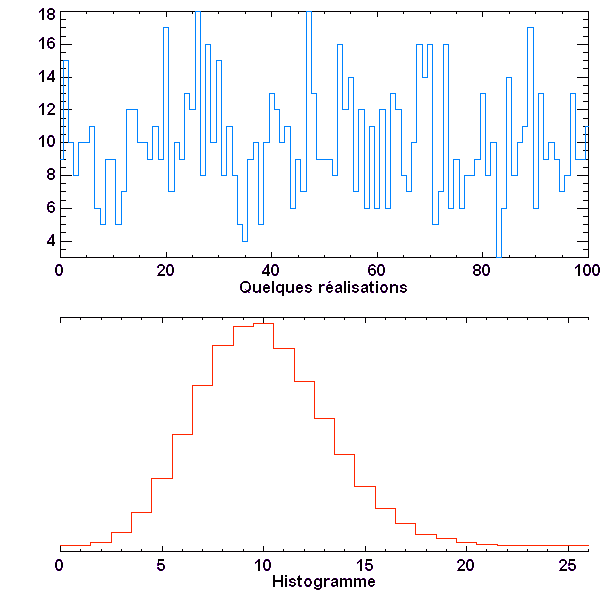
Série de valeurs et histogramme, dans le cas N = 10
Crédit :
ASM
Distribution de Poisson
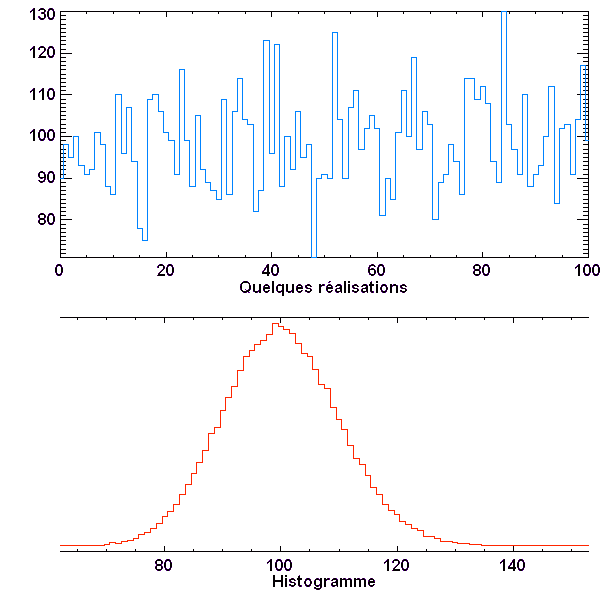
Série de valeurs et histogramme, dans le cas N = 100
Crédit :
ASM
Distribution de Poisson
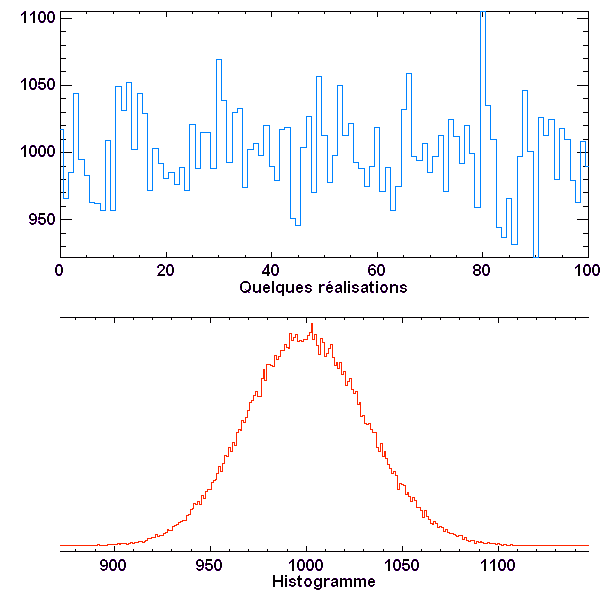
Série de valeurs et histogramme, dans le cas N = 1000
Crédit :
ASM
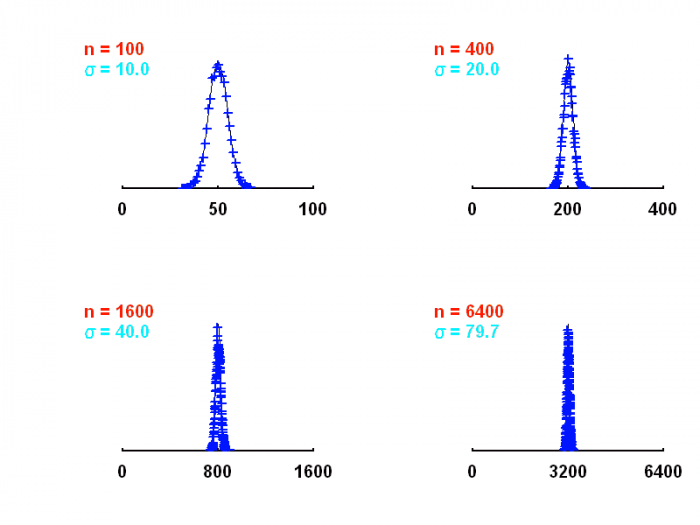
Statistiques poissonniennes. La dispersion relative décroît avec le nombre de quanta attendus.
Crédit :
ASM
 Objectifs
Objectifs
La statistique de Poisson concerne un phénomène régulier quantifié.
La détection d'un rayonnement électromagnétique en est un exemple concret, l'arrivée d'énergie étant quantifiée en photons.
Plus le nombre de photons attendus est grand, mieux on pourra préciser la valeur moyenne observée.
Un exemple concret... et discret
La statistique de Poisson va être abordée via un cas concret. L'analyse de l'arrivée de photons d'une signal lumineux de moyenne constante.
Un rayonnement monochromatique de fréquence 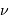 de luminosité
de luminosité 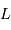 , observé pendant une durée
, observé pendant une durée 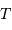 , apporte une énergie
, apporte une énergie 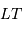 . Ce rayonnement est véhiculé par un nombre moyen de photons
. Ce rayonnement est véhiculé par un nombre moyen de photons 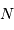 obéissant à :
obéissant à :
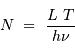
La discrétisation du flux en quanta d'énergie implique que le nombre de photons arrivant par intervalle de temps fluctue autour de cette valeur moyenne.
Extrapolation aux grandes valeurs
Pour les grandes valeurs de 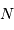 , on peut montrer que cette loi se confond très rapidement avec la gaussienne :
, on peut montrer que cette loi se confond très rapidement avec la gaussienne :
![p(n) \ \propto \ \exp \left[ - {(n-N)^2 \over 2 N}\right]](../pages_analyser/equations_bruit-poisson/equation32.png)
On en conclut alors, en se basant sur la statistique gaussienne, que pour une valeur moyenne 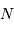 , l'écart-type vaut
, l'écart-type vaut 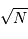 .
.
Il en résulte un point important : lorsque 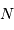 croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
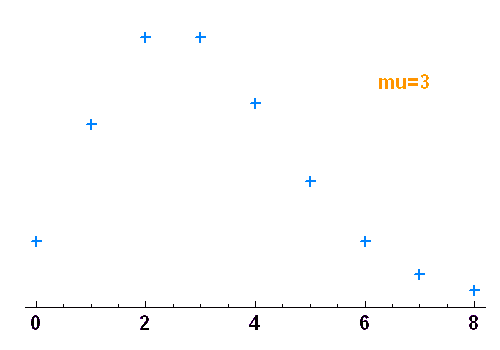
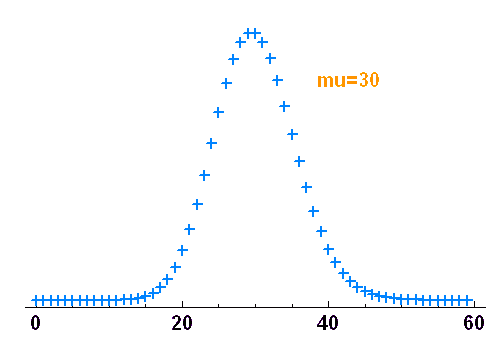
Distribution de Poisson
A l'aide de l'appliquette : tracer une distribution de Poisson, et identifier les variations majeures lorsque la moyenne 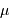 varie.
varie.

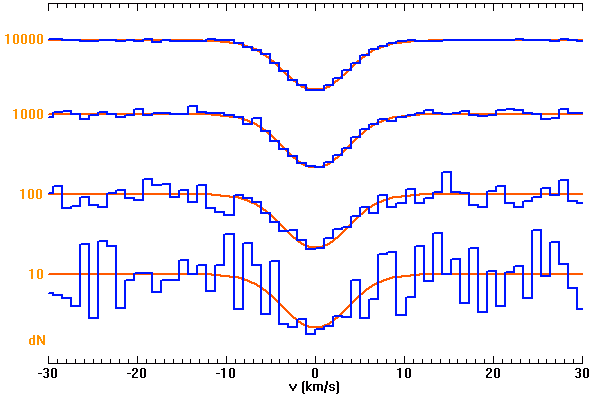
Simulation de la détection d'une raie, en fonction du nombre de photoélectrons dN détectés par intervalle spectral, en supposant la détection limitée par le seul bruit de photons. L'échelle spectrale est donnée en vitesse.
Crédit :
ASM
Bruit de photons et photodétection
Une bonne détection, par exemple l'identification d'une raie spectrale, nécessite l'enregistrement d'un nombre suffisant de photoélectrons, afin que la statistique d'arrivée des photons, de type poissonnien, n'empêche pas la détection.
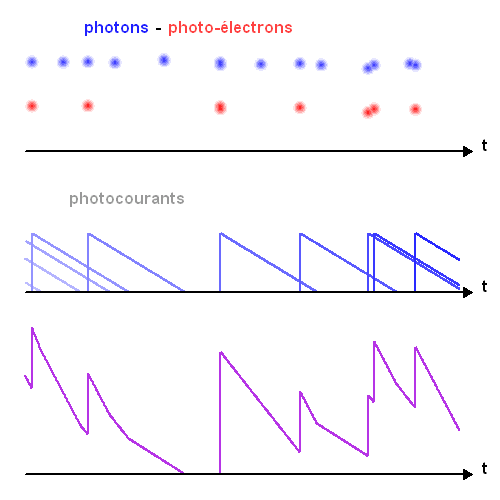
Distribution en fonction du temps de
l'arrivée de photons, des photoélectrons créés et du photocourant résultant. Les photons (points bleus) n'arrivent pas à intervalles de temps réguliers. Seuls un certain nombre d'entre eux donnent naissance à des photoélectrons (points rouges). Le photocourant total (bleu) résulte de la somme des contributions individuelles (couleur variable).
Crédit :
ASM
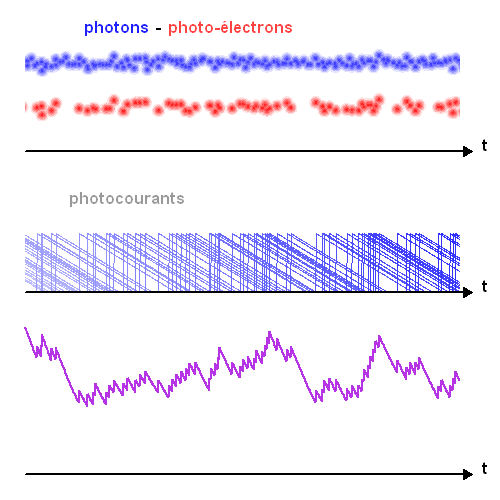
Distribution en fonction du temps de
l'arrivée de photons, des photoélectrons créés et du photocourant résultant. Les photons (points bleus) n'arrivent pas à intervalles de temps réguliers. Seuls un certain nombre d'entre eux donnent naissance à des photoélectrons (points rouges). Le photocourant total (bleu) résulte de la somme des contributions individuelles (couleur variable).
Crédit :
ASM
Photons et photoélectrons
Le bruit de photons est en fait un bruit... de photoélectrons.
L'arrivée dispersée des photons, conjuguée à la conversion aléatoire d'un photon en photoélectron, construisent la statistique de création de photoélectrons, qui dépend bien sûr du nombre de photons.
 Prérequis
Prérequis
Statistique de Poisson : le bruit de photons obéit à la statistique de Poisson.
 Objectifs
Objectifs
Evaluer le bruit et le rapport signal à bruit du bruit de photons.
Statistique de Poisson
La statistique d'arrivée des photons est poissonnienne, vu que les photons sont par définition des quanta d'énergie.
Lorsque l'on attend 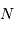 photons par intervalle de temps, la valeur moyenne observée est ...
photons par intervalle de temps, la valeur moyenne observée est ... 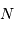 et sa fluctuation autour de cette valeur moyenne vaut
et sa fluctuation autour de cette valeur moyenne vaut 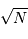 .
.
Il s'ensuit un rapport signal à bruit déterminé par le flux de photons égal à :
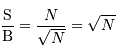
Ce rapport signal à bruit croît avec la racine carrée du nombre de photons collectés.
Photoélectrons
Les photons que l'on observe sont le plus souvent traduits par le détecteurs en photoélectrons, qui suivent la même statistique que les photons, à un facteur de rendement près inférieur à l'unité.
Avec 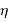 le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
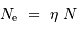
Le bruit de photoélectrons et le rapport signal à bruit résultant valent en pratique 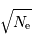 .
.
 Le projet COROT
Le projet COROT
Difficulté : ☆
Temps : 20 min
Question 1)
En supposant que le rendement de la chaîne de détection vaut l'unité, combien de photons doivent être enregistrés pour que le bruit de photons permette une détection à 1 ppm
Avec 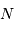 photons, le rapport signal à bruit du bruit de photons vaut
photons, le rapport signal à bruit du bruit de photons vaut 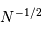 .
.
Question 2)
Le rendement de la chaîne de détection est de 25% seulement. Par quel facteur doit on corriger le nombre de photons à collecter.
Avec 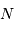 photons, on obtient seulement
photons, on obtient seulement 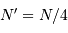 photoélectrons.
photoélectrons.
Question 3)
Le nombre de photons requis est collecté en 5 jours. En déduire le nombre de photons accumulés en une pose élémentaire de 1 minute, et la performance atteinte sur une pose élémentaire.
1 jour = 86400 s = 1440 min
 Au photon près
Au photon près
Difficulté : ☆
Temps : 20 min
La figure ci-jointe représente la courbe de lumière de l'étoile HD 49933, l'une des cibles principales du satellite CoRoT. Le signal stellaire est composé de multiples signaux (activité, oscillations...) et bien sûr du bruit de photons. On admet que celui-ci domine à haute fréquence.
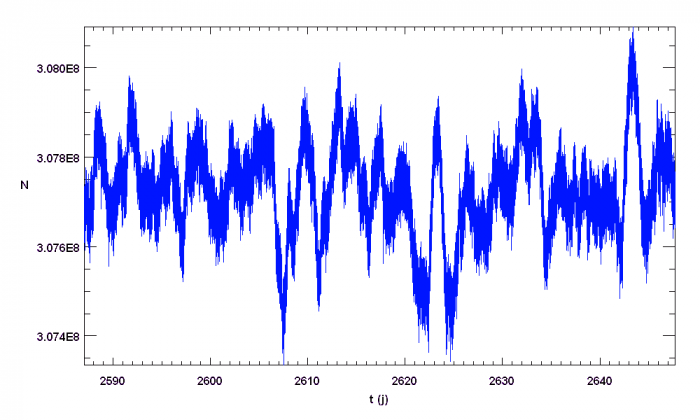
Courbe de lumière de l'étoile HD 49933. Nombre de photo-électrons collectés par seconde en fonction du temps.
Crédit :
ASM/CNES
Question 1)
Estimer l'amplitude totale du bruit du signal stellaire.
[1 points]
Repérer un intervalle de temps où le signal n'évolue pas à basse fréquence, et mesurer l'amplitude crête à crête.
Question 2)
Estimer l'écart-type du bruit
[1 points]
Revoir les propriétés du bruit poissonnien.
Question 3)
Montrer que le bruit mesuré est du même ordre de grandeur que le bruit de photons.
[1 points]
Dérive instrumentale
Les bruits instrumentaux sont souvent dus à des dérives thermiques.
L'exemple ci-joint montre la dérive enregistrée par un astérosismomètre, observant de jour une source de laboratoire délivrant un signal de référence absolument fixe, mais dont la température de travail n'est pas fixée.
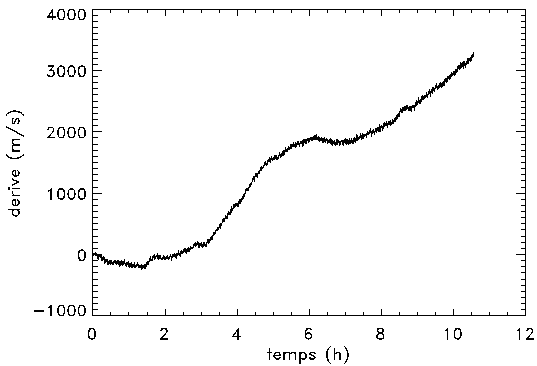
Dérive thermique enregistrée par l'instrument FTS du
CFH, observant de jour une source stabilisée. Les variations de température de la source (mal) stabilisée se traduisent en signal Doppler au cours d'une journée de test. L'inertie thermique joue le rôle de mémoire : le bruit à un instant donné dépend intimement des instants précédents.
Crédit :
ASM/CFHT
Bruit en 1/f
L'effet de mémoire occasionne un bruit instrumental dit en 1/f.
Son évolution temporelle se distingue d'un bruit blanc par une sensible dérive.
Comme le montre l'analyse de Fourier, son spectre de puissance se caractérise alors par une forte contribution aux basses fréquences, qui apparaît clairement
pour un spectre tracé en échelle logarithmique.
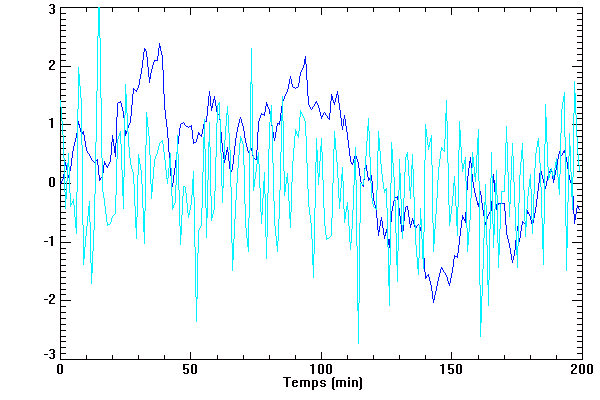
Séries temporelles, correspondant à une bruit blanc (courbe bleu ciel), de moyenne nulle, et à un bruit instrumental en 1/f (courbe bleu foncé) qui dérive.
Crédit :
ASM

Les spectres de puissance des
séries temporelles de différents types de bruits diffèrent sensiblement. Le bruit gaussien n'a pas de fréquence privilégiée, contrairement au bruit instrumental qui montre un spectre de puissance en
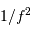
, càd un spectre de Fourier en
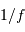
.
Crédit :
ASM
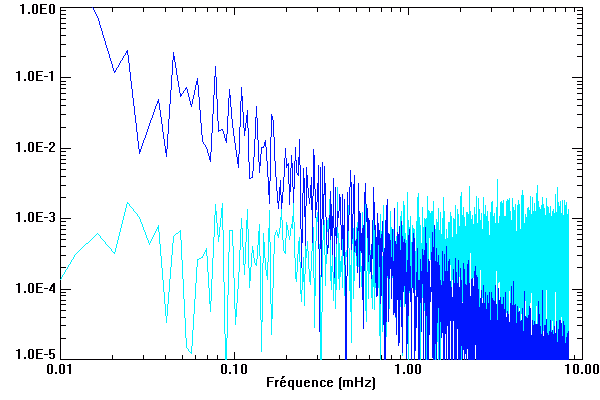
Idem, mais en double échelle logarithmique.
Crédit :
ASM
 Objectifs
Objectifs
Le bruit instrumental est un bruit qui "a de la mémoire". Sa signature spectrale est intense à basse fréquence.
Bruit en 1/f
Le bruit dit en 1/f, avec une dépendance spectrale variant en raison inverse de la fréquence, est typiquement d'origine instrumentale. Il apparaît lorsque les fluctuations induites sur le signal ne sont pas indépendantes, mais corrélées. C'est typiquement le cas des fluctuations thermiques : une perturbation en température à l'instant 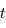 aura des conséquences à tout instant suivant.
aura des conséquences à tout instant suivant.
La transformée de Fourier de l'évolution temporelle d'un tel bruit montre un spectre en 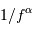 , l'exposant
, l'exposant 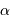 dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.
dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.
Analyse en fréquence d'un bruit instrumental
L'analyse de Fourier d'un bruit en 1/f se caractérise, comme son l'indique, par une forte contribution aux basses fréquences. Ceci apparaît clairement
pour un spectre tracé en échelle logarithmique.
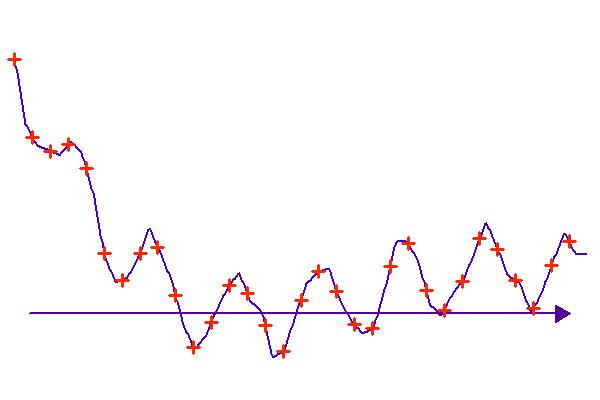
Fonction continue et signal discret associé.
Crédit :
ASM
Continu / discret
Un signal continu n'existe pas : décrire le continu nécessite une infinité de valeurs. Tout signal est échantillonné, càd décrit sur un nombre discret de valeurs.
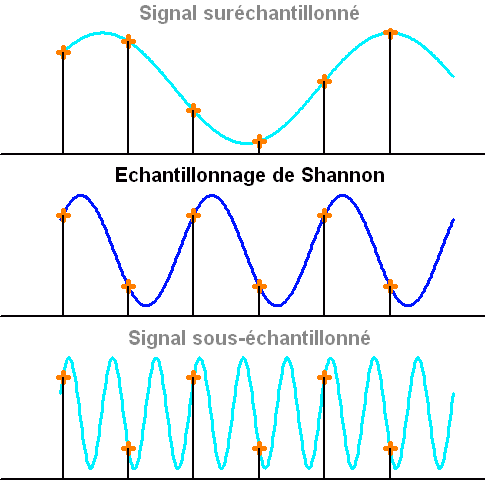
Un signal simple est échantillonné à la limite de Shannon avec 2 points par période. L'information d'un signal sous-échantillonné est perdue.
Crédit :
ASM
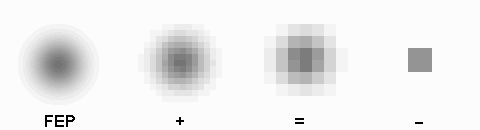
L'image initiale (cadre de gauche) est échantillonnée sur un nombre décroissant de pixels. Toute l'information utile est préservée dès lors que la fonction d'étalement du point est convenablement échantillonnée (=). Trop d'informations est inutile (+), et pas assez est destructif (-).
Crédit :
ASM
Échantillonnage de Shannon
Un détecteur ayant une résolution limite (spatiale ou temporelle), un signal physique est nécessairement échantillonné. Même si une observation avec ce détecteur semble prendre des valeurs continues, elle peut être traduite par une série finie de valeurs, correspondant à un échantillonnage discret.
Une bonne observation nécessite de ne pas dégrader la résolution du signal par ce phénomène d'échantillonnage, ce qu'exprime la condition d'échantillonnage de Shannon, qui s'applique aussi pour un signal 2-D.
Coupure
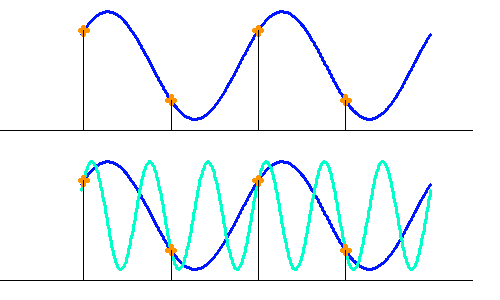
Il est nécessaire d'échantillonner au moins 2 points par période. L'échantillonnage définit ainsi une valeur maximale des fréquences analysables.
Au-delà de la fréquence de coupure, un signal de fréquence plus rapide que la fréquence de coupure peut se confondre avec un signal de pulsation moindre.
Crédit :
ASM
Echantillonnage et coupure
Le pas d'échantillonnage détermine la résolution maximale en fréquence. Au delà de la fréquence de coupure, échantillonnée sur 2 points par période, l'information est perdue. Autrement dit, la fréquence de coupure définie selon Fourier et le théorème de Shannon rendent compte du même phénomène.
Echantillonnage
Tout signal, spatial ou temporel, est limité en fréquence, à cause du processus d'observation. Il peut être codé sur une distribution discrète de valeurs. Ce processus de discrétisation est nommé échantillonnage.
Théorème de Shannon
Le critère de Shannon énonce qu'un signal doit avoir sa fréquence maximale échantillonnée sur au-moins 2 pixels afin de ne subir aucune dégradation.
En pratique, il faut :
- 2 acquisitions temporelles par période pour un signal temporel périodique
- 2 pixels par élément de résolution spatiale pour un signal spatial
La justification de ce critère est liée à l'analyse fréquentielle, par transformée de Fourier : en appliquant le critère de Nyquist, les fréquences sont restituées convenablement jusqu'à la fréquence de coupure.
 Choix d'un détecteur
Choix d'un détecteur
Difficulté : ☆
Temps : 10 min
Un télescope de la classe 4-m, dans une configuration ouverte à f/2, est installé dans un site dont le meilleur seeing est aux alentours de 0.5" en lumière visible. Une caméra CCD installée pour des programmes d'imagerie est spécifiée pour imager sans perdre d'éléments d'information.
Question 1)
Quel paramètre de la caméra est crucial pour satisfaire la spécification donnée ?
L'ouverture du faisceau est déterminée, ainsi que la résolution angulaire. Ceci permet de déterminer la résolution spatiale dans le plan focal.
Question 2)
Sur catalogue, on trouve des caméras avec des pixels de 9, 15 ou 25 microns. Quel choix effectuer ?
Question 3)
Un système d'optique adaptative permet d'atteindre la limite théorique de diffraction dans l'IR à 2 microns. Sachant qu'il n'existe pas de caméra avec des pixels plus petits que 9 micromètres, quel paramètre de la chaîne de collecte du signal doit évoluer ?
Déterminer la tache de diffraction à 2 micromètres.
Identifier les paramètres fixes, de ceux qui le sont moins...
 Signal sismique
Signal sismique
Difficulté : ☆
Temps : 10 min
On cherche à caractériser un spectre d'oscillations stellaires. La période minimale des oscillations stellaires est de 4 minutes, et on souhaite distinguer des fréquences avec une résolution de 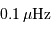 .
.
Question 1)
Estimer la durée totale nécessaire pour ce programme.
[1 points]
Question 2)
Déterminer l'échantillonnage temporel optimal, qui permette de ne pas filtrer les hautes fréquences et minimise le nombre final de données.
[1 points]
Question 3)
Les séquences d'observation du satellite COROT (projet CNES) sont-elles en accord, avec un point de mesure toutes les 32 s et 150 jours d'observation continue sur une cible stellaire ?
[1 points]
- Question 1
Aide :
Au numérateur, on a tout simplement le signal, au dénominateur les bruits.
Aide :
Il reste à identifier le terme 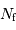 et à interpréter la somme du dénominateur.
et à interpréter la somme du dénominateur.
Solution :
Les 3 termes du dénominateur sont :
- le bruit de photons 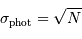 ,
,
- le bruit de fond, 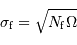 , avec
, avec 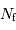 le nombre de photoélectrons par unité d'angle solide dus au fond,
le nombre de photoélectrons par unité d'angle solide dus au fond,
- le bruit de lecture.
- Question 2
Aide :
Déterminer l'importance relative des différents bruits.
Solution :
Pour un objet très brillant, le bruit de photons de la source va dominer devant les autres bruits :
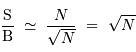
Dans le cas d'un objet peu lumineux, le bruit de photons de la source est négligeable. En l'absence d'autres données, il n'est pas possible de discriminer parmi les 2 autres sources de bruit.
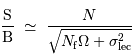
Dans un cas, 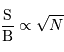 , dans l'autre
, dans l'autre 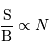 .
.
- Question 3
Aide :
Comment le nombre de photoélectrons collectés varie-t-il avec le diamètre du collecteur ou le temps de pose ?
Solution :
Si l'on note 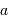 le diamètre du collecteur et
le diamètre du collecteur et 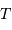 le temps de pose, il est immédiat que
le temps de pose, il est immédiat que 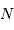 varie comme la surface collectrice
varie comme la surface collectrice 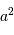 et comme
et comme 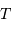 .
.
On en déduit les dépendances respectives :
| diamètre collecteur | temps de pose |
| source lumineuse | 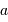 | 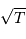 |
| source faible | 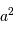 | 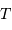 |
Dépendance envers 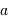 ou
ou 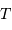 du rapport signal à bruit.
du rapport signal à bruit.
- Question 1
Aide :
L'ouverture du faisceau est déterminée, ainsi que la résolution angulaire. Ceci permet de déterminer la résolution spatiale dans le plan focal.
Solution :
L'ouverture du faisceau étant déterminée, la focale du télescope est connue (8 m) ainsi que la résolution angulaire, limité par le seeing 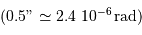 , la taille linéaire dans le plan focal est fixée :
, la taille linéaire dans le plan focal est fixée :
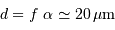
- Question 2
Solution :
La taille des pixels doit être au moins moitié moindre que la tache de seeing, il faut donc des pixels de 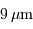 .
.
- Question 3
Aide :
Déterminer la tache de diffraction à 2 micromètres.
Aide :
Identifier les paramètres fixes, de ceux qui le sont moins...
Solution :
La tache de diffraction vaut 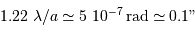 . Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
. Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
Comme le diamètre du télescope est fixée, de même que la taille minimale des pixels, la seule variable d'ajustement est l'ouverture du faisceau. Elle doit être diminuée d'un facteur au-moins 5, passant de f/4 à f/20.








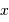 suit une loi de Poisson de moyenne
suit une loi de Poisson de moyenne 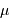 si la probabilité pour réaliser
si la probabilité pour réaliser 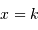 vaut
vaut 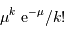





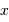 va être donnée par
va être donnée par 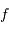 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 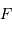 sa fonction de répartition
sa fonction de répartition 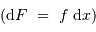 .
.
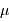 la moyenne et
la moyenne et 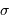 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
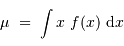
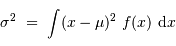
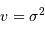 est la variance).
est la variance).


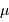 de la densité de probabilité de sa mesure
de la densité de probabilité de sa mesure 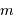 . Avec
. Avec 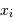 les réalisations d'une variable aléatoire, on a accès seulement à :
les réalisations d'une variable aléatoire, on a accès seulement à :
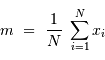
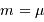 . En fait, c'est de mieux en mieux réalisé lorsque
. En fait, c'est de mieux en mieux réalisé lorsque 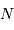 devient très grand.
devient très grand.
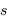 est mesurable par :
est mesurable par :
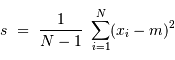
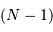 au dénominateur car
au dénominateur car 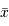 a déjà été obtenu à l'aide des
a déjà été obtenu à l'aide des 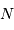 mesures, et il ne reste plus que
mesures, et il ne reste plus que 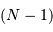 valeurs indépendantes pour estimer
valeurs indépendantes pour estimer 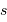 .
.
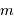 et
et 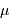 vaut typiquement
vaut typiquement 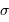 .
.

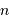 points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.
points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.

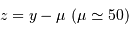 et puis
et puis 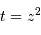 . L'ajustement donne un écart-type de 1.
. L'ajustement donne un écart-type de 1.

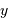 n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0
n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0 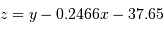 et puis
et puis 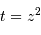 . L'ajustement donne un écart-type de 1.04.
. L'ajustement donne un écart-type de 1.04.

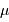 , et celle du bruit par l'écart-type
, et celle du bruit par l'écart-type 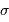 . Le rapport signal à bruit est donc :
. Le rapport signal à bruit est donc :
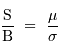
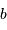 , il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
, il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
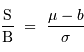
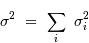
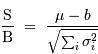


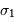 et
et 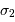 a un écart-type de :
a un écart-type de :
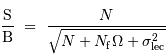
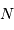 le nombre de photoélectrons reçus,
le nombre de photoélectrons reçus, 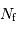 relié à un signal de fond,
relié à un signal de fond, 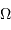 la taille angulaire de la cible, et
la taille angulaire de la cible, et 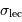 le bruit de lecture
le bruit de lecture
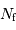 et à interpréter la somme du dénominateur.
et à interpréter la somme du dénominateur.
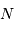 du rapport signal à bruit.
du rapport signal à bruit.
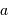 du collecteur ou le temps de pose
du collecteur ou le temps de pose 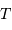 .
.

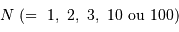 variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque
variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque 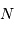 augmente, la distribution tend vers une loi gaussienne de moyenne
augmente, la distribution tend vers une loi gaussienne de moyenne 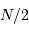 et écart type
et écart type 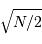 (courbe rouge). Pour
(courbe rouge). Pour 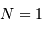 , la distribution reste bien sûr uniforme,
pour
, la distribution reste bien sûr uniforme,
pour 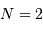 elle garde une allure triangulaire.
elle garde une allure triangulaire.

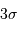

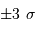 de la moyenne.
de la moyenne.
![f(x) \ = \ {1\over \sqrt{2\pi}\sigma}\ \exp \left[ -{(x-\mu)^2\over 2 \sigma^2} \right]](../pages_analyser/equations_bruit-gaussien/equation9.png)
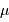 la moyenne et
la moyenne et 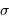 l'écart-type. Un tel bruit est dit gaussien.
l'écart-type. Un tel bruit est dit gaussien.
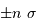 par rapport à la valeur moyenne décroît rapidement avec
par rapport à la valeur moyenne décroît rapidement avec 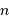 ;
99.7 % des réalisations du signal s'écartent de moins de
;
99.7 % des réalisations du signal s'écartent de moins de 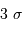 de la moyenne.
de la moyenne.
![[-n\ \sigma, \ n \ \sigma]](../pages_analyser/equations_bruit-gaussien/equation15.png) pour un bruit gaussien.
pour un bruit gaussien.
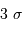 de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?


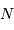 pas, il se sera éloigné du lampadaire d'une distance moyenne de
pas, il se sera éloigné du lampadaire d'une distance moyenne de 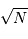 .
.

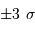 . On en déduit un niveau de bruit de l'ordre de 16/6=2.7. Le signal moyen étant d'environ 200, le rapport signal à bruit est voisin de 75.
. On en déduit un niveau de bruit de l'ordre de 16/6=2.7. Le signal moyen étant d'environ 200, le rapport signal à bruit est voisin de 75.

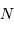 quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de
quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de 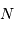 . La distribution des valeurs dépend du nombre N :
. La distribution des valeurs dépend du nombre N :
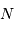 est grand, plus la
est grand, plus la 



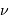 de luminosité
de luminosité 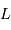 , observé pendant une durée
, observé pendant une durée 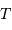 , apporte une énergie
, apporte une énergie 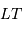 . Ce rayonnement est véhiculé par un nombre moyen de photons
. Ce rayonnement est véhiculé par un nombre moyen de photons 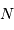 obéissant à :
obéissant à :
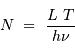
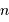 photons lorsque
photons lorsque 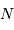 sont attendus en moyenne s'écrit :
sont attendus en moyenne s'écrit :
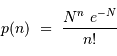
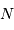 .
Il faut retenir que :
.
Il faut retenir que :
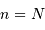 .
.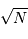 .
.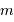 parties, suffisamment petites pour assurer qu'un seul photon peut arriver pendant l'intervalle de temps
parties, suffisamment petites pour assurer qu'un seul photon peut arriver pendant l'intervalle de temps 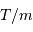 , on peut estimer la probabilité de voir arriver
, on peut estimer la probabilité de voir arriver 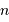 photons, en les rangeant dans les
photons, en les rangeant dans les 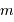 cases.
cases.
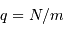 , et la probabilité opposée
, et la probabilité opposée 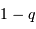 . Comme il y a
. Comme il y a 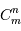 façons de ranger
façons de ranger 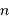 photons dans les
photons dans les 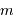 cases, on obtient finalement en développant le coefficient de combinaison :
cases, on obtient finalement en développant le coefficient de combinaison :
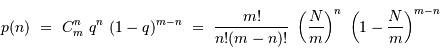
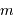 d'intervalles, on retrouve la loi énoncée :
d'intervalles, on retrouve la loi énoncée :
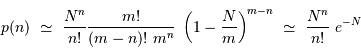
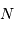 grand et
grand et 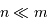 :
:
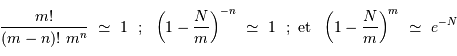
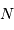 , on
, on ![p(n) \ \propto \ \exp \left[ - {(n-N)^2 \over 2 N}\right]](../pages_analyser/equations_bruit-poisson/equation32.png)
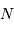 , l'écart-type vaut
, l'écart-type vaut 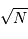 .
.
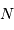 croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
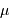 varie.
varie.



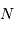 photons par intervalle de temps, la valeur moyenne observée est ...
photons par intervalle de temps, la valeur moyenne observée est ... 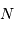 et sa fluctuation autour de cette valeur moyenne vaut
et sa fluctuation autour de cette valeur moyenne vaut 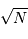 .
.
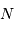 photons, est
photons, est 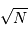 .
.
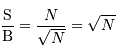
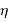 le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
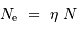
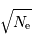 .
.
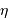 le rendement du détecteur. Le rapport signal à bruit varie comme
le rendement du détecteur. Le rapport signal à bruit varie comme 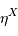 avec
avec 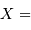 :
:
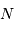 photons, le rapport signal à bruit du bruit de photons vaut
photons, le rapport signal à bruit du bruit de photons vaut 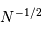 .
.
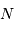 photons, on obtient seulement
photons, on obtient seulement 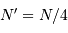 photoélectrons.
photoélectrons.



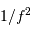 , càd un spectre de Fourier en
, càd un spectre de Fourier en 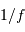 .
.

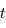 aura des conséquences à tout instant suivant.
aura des conséquences à tout instant suivant.
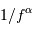 , l'exposant
, l'exposant 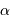 dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.
dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.


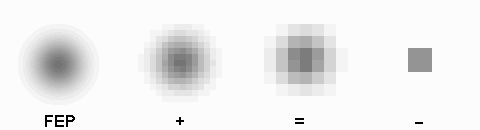

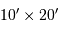 avec une résolution de 0.6",
il faut une caméra de taille (en pixels) :
avec une résolution de 0.6",
il faut une caméra de taille (en pixels) :
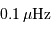 .
.
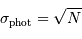 ,
,
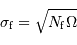 , avec
, avec 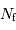 le nombre de photoélectrons par unité d'angle solide dus au fond,
le nombre de photoélectrons par unité d'angle solide dus au fond,
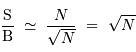
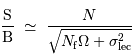
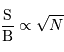 , dans l'autre
, dans l'autre 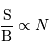 .
.
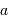 le diamètre du collecteur et
le diamètre du collecteur et 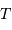 le temps de pose, il est immédiat que
le temps de pose, il est immédiat que 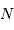 varie comme la surface collectrice
varie comme la surface collectrice 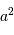 et comme
et comme 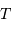 .
.
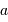
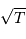
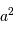
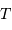
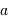 ou
ou 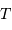 du rapport signal à bruit.
du rapport signal à bruit.
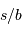 et la performance requise sont tous deux exprimés dans le même système d'unité relative. Le nombre
et la performance requise sont tous deux exprimés dans le même système d'unité relative. Le nombre 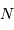 de photons doit donc vérifier :
de photons doit donc vérifier :
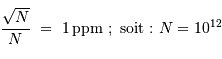
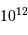 photons pour atteindre la sensibilité requise.
photons pour atteindre la sensibilité requise.
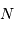 photons, on obtient seulement
photons, on obtient seulement 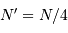 photoélectrons. L'égalité précédente doit donc être vérifiée par
photoélectrons. L'égalité précédente doit donc être vérifiée par 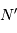 et non par
et non par 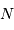 . Il faut donc collecter
. Il faut donc collecter 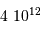 photons.
photons.
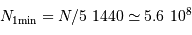
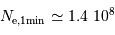 photo-électrons), la performance devient
photo-électrons), la performance devient 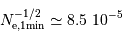 .
.
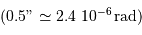 , la taille linéaire dans le plan focal est fixée :
, la taille linéaire dans le plan focal est fixée :
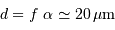
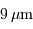 .
.
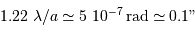 . Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
. Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.