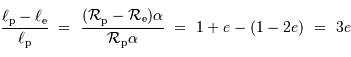Les unités définies dans les chapitres précédents reposent sur l'observation de phénomènes périodiques, par rotation (l'année, la circonférence de la Terre...). Mais en fait, si l'on scrute ces phénomènes plus précisément, leur définition se doit d'être approfondie.

Définition du mètre.
Crédit :
Bibliothèque de l'Observatoire de Paris
L'équation du temps
La définition du jour est basée sur la rotation de la Terre, et mesurée par le passage au méridien du soleil, qui définit un intervalle de temps de 24 heures. Et pourtant !
Si l'on repère chaque jour le passage au méridien du soleil, et que l'on repère cet instant par rapport à une valeur moyenne, on note au fil de l'année une
modulation. Midi arrive en avance ou en retard, avec une amplitude de l'ordre d'un quart d'heure au plus, due à la variation du mouvement annuel de la Terre autour du Soleil.
Cette modulation peut être observée à toute heure.
Equation du temps

Superpositions d'images du soleil, à heure locale fixe, par pas de 10 jours. La direction de l'appareil de mesure est fixe, l'avance ou le retard du soleil vrai par rapport au soleil moyen crée cette figure en 8.
Crédit :
Observatoire de Naucsny, Crimée/V. Rumyantser
Cadran solaire avec l'équation du temps
Cadran solaire avec correction de l'équation du temps.
Crédit :
ASM
A l'équinoxe
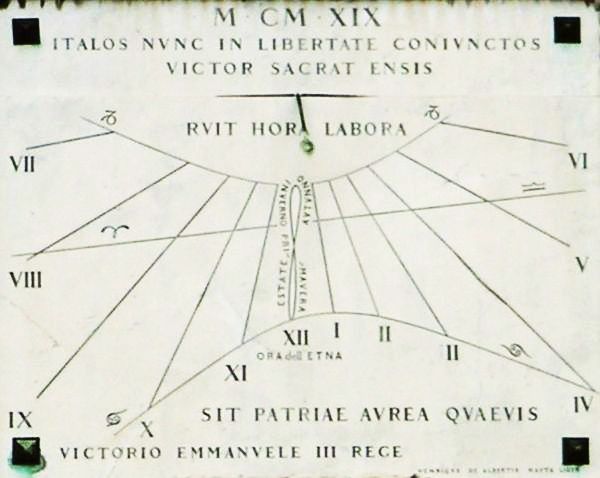
L'équation du temps correspondant à un déphasage entre midi solaire et midi local moyen, les lever et coucher du soleil sont également déphasés. Ceci est particulièrement sensible au voisinage d'un solstice. Ce n'est pas pile au solstice d'été (d'hiver) que
le soleil se lève le plus tôt (tard) et se couche le plus tard (tôt)... mais c'est bien aux solstices que la durée du jour est extrêmale.
Heure (TU) des levers et couchers du Soleil aux alentours du solstice d'hiver. Si la durée du jour est bien minimale le 21 décembre, c'est 10 jours avant le solstice que le soleil se couche le plus tôt, et 10 jours après qu'il se lève le plus tard.
Crédit :
ASM
Midi à quelle heure ?
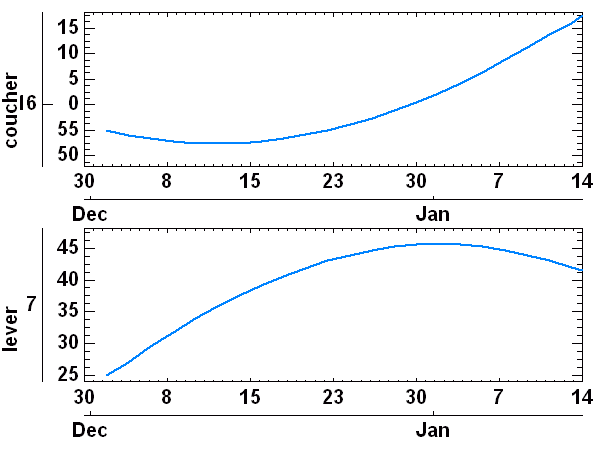
Equation du temps
La courbe de décalage du midi solaire par rapport au midi local a deux composantes. La première, de période annuelle est due à l'ellipticité de la l'orbite terrestre (courbe bleue) et la deuxième, semestrielle, est due à l'obliquité de son axe de rotation (courbe verte).
Crédit :
ASM
Les 24 heures séparant deux midis solaires dépendent de la rotation propre de la Terre. Comme son orbite n'est pas circulaire, l'entraînement n'est pas régulier (cf. 2ème loi de Kepler).
Il s'ensuit un phénomène appelé équation du temps : midi n'arrive pas à midi régulièrement.
Quelle époque ?
Les étoiles n'ont pas la réputation d'être volages, et pourtant
on voit dans la littérature des coordonnées différentes pour un même objet, repérées par des dates différentes.
Des époques standard ont été définies, pour s'y retrouver.
C'est la précession de l'axe polaire qui explique la majeure part des dérives repérées.

Données du catalogue Vizier pour l'étoile Albireo. Remarquer la dérive des coordonnées au fil du temps.
Crédit :
CDS

Fenêtre de l'interface du programme Vizier du CDS (Centre de Données Stellaires), questionnant l'identité des coordonnées proposées.
Crédit :
CDS
Quelle année ?
L'orbite de la Terre n'est ni circulaire, ni rigoureusement elliptique (malgré ce que nous a appris Newton).
L'axe de rotation de la Terre n'est pas fixe, mais animé d'un mouvement de précession (de période 26000 ans), car il
évolue sous l'effet de termes gravitationnels non inclus dans le problème à 2 corps, dus par exemple au fait que la Terre n'est pas un point matériel. Il s'ensuit que
les coordonnées angulaires d'un astre évoluent dans le temps. Elles sont données pour une époque de référence (p.ex. 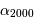 ,
, 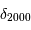 ).
).
Coordonnées aux époques 1950 et 2000 de l'étoile Véga.
Il s'ensuit diverses définitions de l'année, selon que l'on se réfère à l'intervalle de temps entre 2 solstices, 2 périhélies, 2 passages au point vernal.
On définit ainsi des années de durées légèrement différentes. Pour plus de précision, voir le site de l'Institut de Mécanique Céleste
Quelle référence pour les coordonnées angulaires ?
Les coordonnées polaires, c'est simple a priori. Sauf que faire les mesures à partir de la surface de la Terre, et non du centre, change le point de vue.
La Terre n'étant pas ronde, la définition des coordonnées angulaires par rapport à la verticale locale ne coincide pas avec une définition centrale.
Coordonnées géographique et géocentrique
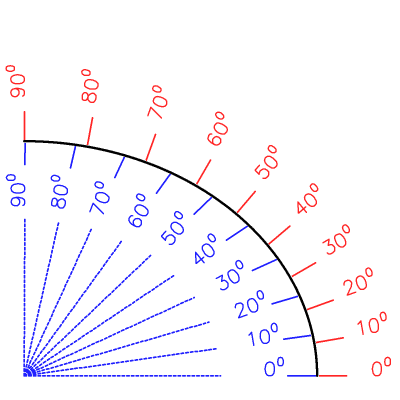
Double définition possible des coordonnées angulaires à la surface d'un objet en forme d'ellipsoïde aplati (tel que la Terre). Les coordonnées géocentriques (bleu) sont définies par rapport au centre de l'objet ; les coordonnées géographiques (rouge) par rapport à la verticale locale.
Crédit :
ASM
 La figure de la Terre
La figure de la Terre
Difficulté : ☆☆
Temps : 30 min
Au milieu du XVIIIe siècle, les missions de La Condamine au Pérou et de Maupertuis au Laponie ont conduit à la mesure de la longueur d'un degré du méridien en Laponie (aux alentours de la latitude 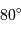 ) ainsi qu'au Pérou (vers
) ainsi qu'au Pérou (vers 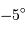 ). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
Question 1)
Expliquer pourquoi la longueur d'un degré le long du méridien diffère entre ces 2 régions. Faire un schéma.
Réfléchir au système de coordonnées utilisé.
Question 2)
La Terre étant aplatie aux pôles, le rayon de courbure local est-il plus important au pôle ou à l'équateur ? Quel degré de méridien correspond à la plus grande longueur ?
Voir la figure de la question précédente.
Question 3)
La longueur 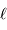 d'un arc de méridien d'ouverture
d'un arc de méridien d'ouverture 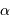 s'écrit en fonction du rayon de courbure
s'écrit en fonction du rayon de courbure 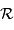 :
:
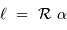
En représentation paramétrique, on repère un point de l'ellipse de révolution par
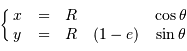
avec 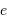 le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en
le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en 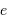 :
:
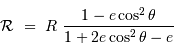
[on peut retrouver ce résultat en appliquant la définition : 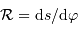 , avec
, avec 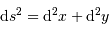 et
et 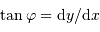 ].
].
Les mesures pour tourner de 1 degré donnant respectivement 57395 toises en Laponie, et 56735 toises au Pérou (57097 au sud de Paris), en déduire
un ordre de grandeur de l'aplatissement de la Terre, exprimé comme la différence relative entre les rayons au pôle et à l'équateur.
Identifier 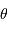 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 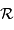 .
.
- Question 1
Aide :
Réfléchir au système de coordonnées utilisé.
Solution :
Les mesures sont effectuées en coordonnées géographiques, les observateurs pouvant p.ex. s'appuyer sur la verticale locale, et non sur une hypothétique et inconnue direction pointant le centre de la Terre.
En raison de la non sphéricité, le rayon de courbure local varie, et donc la mesure d'un arc d'ouverture fixée.
Angles de position géocentrique en bleu, géographique en rouge, repérés pour une équidistance de 10 degrés
Crédit :
ASM
- Question 2
Aide :
Voir la figure de la question précédente.
Solution :
Comme le rayon de courbure local est plus important au pôle, une rotation d'un angle géographique de 10 degré sera plus importante au pôle.
Crédit :
ASM
- Question 3
Aide :
Identifier 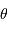 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 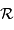 .
.
Solution :
Les rayons de courbures aux pôles 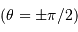 ou à l'équateur
ou à l'équateur 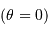 valent respectivement :
valent respectivement :
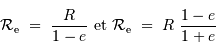
Avec l'hypothèse que  est petit, et les développements limités usuels, on trouve :
est petit, et les développements limités usuels, on trouve :
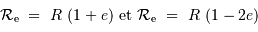
On en déduit que la différence relative des mesures, de l'ordre de 1.2%, correspond à 3 fois le paramètre  . En effet :
. En effet :
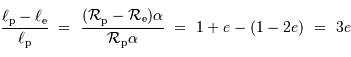
d'où l'aplatissement de la Terre, de l'ordre de 0.4%, cad 1/250.
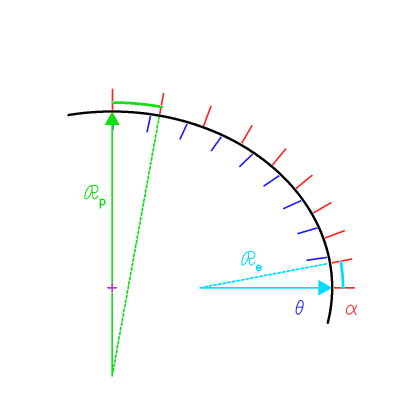
Rayons de courbure à l'équateur et au pôle
Crédit :
ASM







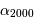 ,
, 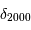 ).
).
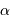
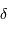
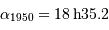
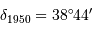
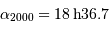
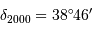

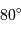 ) ainsi qu'au Pérou (vers
) ainsi qu'au Pérou (vers 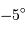 ). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
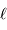 d'un arc de méridien d'ouverture
d'un arc de méridien d'ouverture 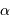 s'écrit en fonction du rayon de courbure
s'écrit en fonction du rayon de courbure 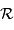 :
:
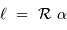
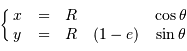
 le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en
le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en 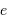 :
:
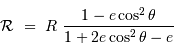
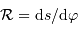 , avec
, avec 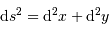 et
et 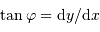 ].
].
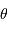 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 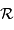 .
.


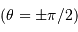 ou à l'équateur
ou à l'équateur 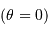 valent respectivement :
valent respectivement :
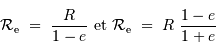
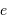 est petit, et les développements limités usuels, on trouve :
est petit, et les développements limités usuels, on trouve :
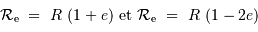
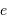 . En effet :
. En effet :