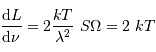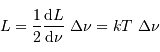La notion de corps noir est simultanément simple et complexe.
Simple, car la situation du corps noir représente une situation d'équilibre thermodynamique entre la matière et son rayonnement. Et l'Univers comme les étoiles sont de bons corps noirs. Complexe, par les pièges du langage - rien de moins noir qu'un corps noir - et par les multiples accrocs à l'équilibre précédemment cité : l'étude d'un spectre stellaire est justement intéressante par ses écarts au corps noir.
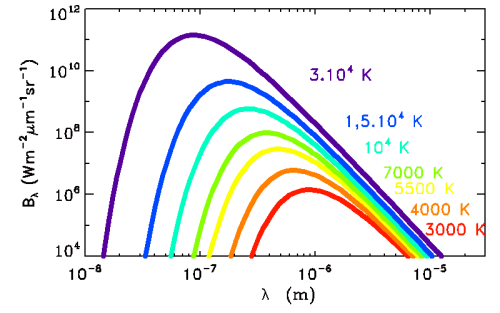
Spectres de corps noirs.
Crédit :
ASM
Le corps noir est ... noir
D'où vient le terme corps noir?
L'étude de quelques documents permet de comprendre cette dénomination.
Notons tout d'abord que l'examen du spectre visible, qui ne comporte
aucune partie noire et brillante, rappelle que le noir est, plutôt qu'une couleur, une absence de couleur.

Les raies en absorption de ce spectre apparaissent noires.
Crédit :
ASM
Un corps absorbant apparaît noir.
Exemples
La photo d'une façade
montre des murs violemment éclairés, et des fenêtres
très sombres dès lors que les vitres sont ouvertes. Il apparaît que les
photons solaires sont bien réfléchis dans un cas, mais dans l'autre ont
singulièrement disparu. Diffusés dans la pièce derrière la vitre, bien
peu de ces photons sont ressortis, et ceci explique le contraste de
luminosité entre la façade et les fenêtres ouvertes.
Façade éclairée

Les fenêtres ouvertes de cette façade ne laissent rien voir de la pièce qu'elles pourraient découvrir. Contrairement aux murs ou aux vitres des fenêtres fermées, qui réfléchissent la lumière incidente, elles renvoient très peu de lumière visible, ce qui explique leur aspect noir.
Crédit :
ASM
Les différents détecteurs, qui ont pour fonction de capter la lumière visible,
apparaissent noirs : ils ne réfléchissent guère la lumière !
Détecteurs optiques

Assemblage de mosaïques CCD pour l'imagerie
grand champ. Un détecteur se doit d'être absorbant, donc le plus noir possible.
Crédit :
CFHT
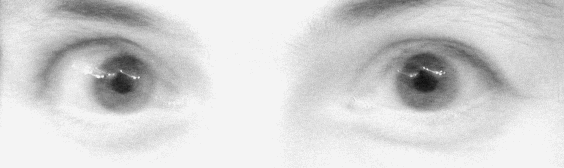
La pupille protégeant la rétine apparaît noire.
Les petites taches brillantes sont des réflexions parasites, qui indiquent que la transmission de la lumière vers les capteurs n'est pas de 100%.
Crédit :
ASM
Les détecteurs optiques
ont pour mission de rendre compte de
l'information lumineuse. Cette opération nécessite l'absorption des
photons. La figure
de quelques détecteurs, dont la pupille de l'oeil humain, montre qu'effectivement
ils apparaissent noirs.
Un corps noir peut être coloré
Une étoile, le Soleil par exemple, est présenté comme un corps noir.
A basse résolution spectrale, le spectre du
soleil se superpose à celui
d'un corps noir de température 5777 K.
Et pourtant rien n'est moins noir que le soleil. Il apparaît donc
nécessaire de donner une définition précise de ce qu'est un corps
noir... qui peut être coloré.
Le spectre du soleil à basse résolution
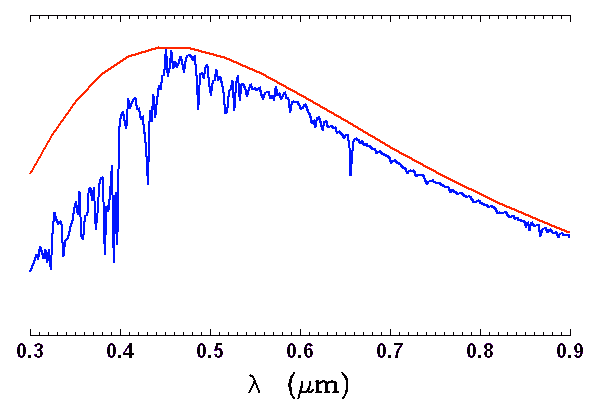
Observé à basse résolution, le spectre du soleil ressemble à celui d'un
corps noir de température d'équilibre 5777 K. Mais pour déterminer cette température au degré près, il est nécessaire d'analyser finement les écarts à la loi du corps noir.
Crédit :
ASM
 Prérequis
Prérequis
- Thermodynamique : équilibre et notion de température
 Objectifs
Objectifs
- Comprendre ce qui caractérise un corps noir
Le corps noir
On trouve comme définitions usuelles du corps noir :
 Définition
Définition
- Un corps noir est un corps idéal
totalement absorbant à toute radiation
électromagnétique.
- Un exemple de corps noir consiste en une enceinte
isotherme munie d'une toute petite ouverture
Ces définitions n'aident pas directement à comprendre pourquoi un corps tel une
étoile est un corps noir. Le lien peut déjà apparaître, si l'on compare
comme dans le chapitre
structure interne
le rapport de 2 durées : celle prise par un photon pour traverser
directement un rayon stellaire, et celle mesurant qu'effectivement
l'énergie produite au sein du soleil est évacuée en surface.
Un exemple : le soleil
La traversée directe du rayon solaire à la vitesse de la lumière prend à peine plus de 2 secondes, alors qu'il faut près
d'un million d'années pour que l'énergie soit extraite du soleil. Cette durée est incomparablement plus longue, car le trajet de l'énergie est une marche au hasard entrecoupée d'incessantes absorptions et réémissions de photons.
Illustration de la marche des photons au sein du soleil
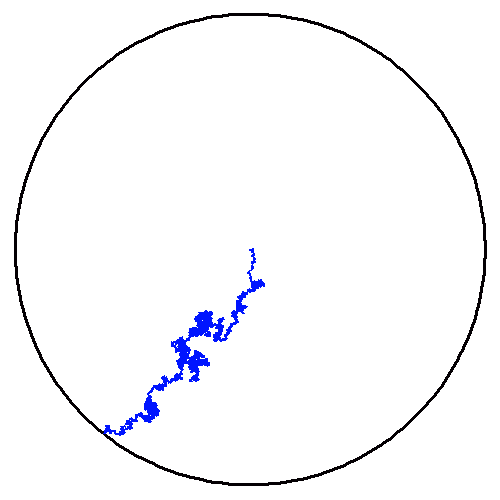
Le processus d'absorption-réémission permet de transporter l'énergie du centre du soleil jusque vers l'extérieur, tout en assurant un équilibre énergétique, qui va conduire au rayonnement de corps noir du soleil.
Crédit :
ASM
En ce sens on comprend que le soleil est très absorbant pour ses propres photons. Son
spectre
a l'allure de celui d'un corps noir. Il est vrai que s'y superposent des raies d'absorption :
- L'allure de corps noir rend compte de l'équilibre
thermique global
- Les raies du spectre rendent compte de la nature de la
matière solaire dans les couches superficielles d'où s'échappent les photons.
Il en résulte qu'un corps noir est défini par l'équilibre intime entre sa matière et son rayonnement. Sa température d'équilibre explicite à elle seule la distribution spectrale de son rayonnement.
Qu'est-ce qu'un corps "pas noir" ?
Plusieurs phénomènes sont irréductibles au corps noirs :
- Un miroir est par définition très réfléchissant, et ne
peut donc pas être absorbant. Il n'y aucun équilibre entre un miroir
et le flux lumineux qu'il réfléchit.
- Le rayonnement émis par une lampe à
vapeur spectrale obéit à des règles de quantification énergétique
fixées par la nature du gaz qui émet le rayonnement. La position des raies d'émission dépend de la nature de l'élément, et pas de la température.
Spectres de corps noirs
L'observation de spectres stellaires, à basse
résolution spectrale montre que l'allure
de ces spectres suit effectivement celle d'un corps noir.
Spectres de corps noirs
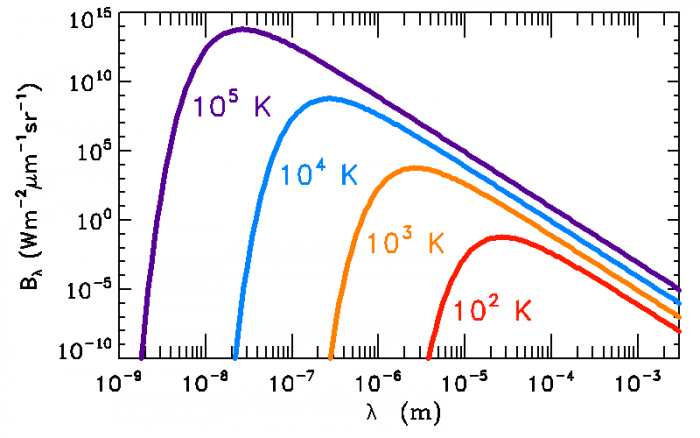
Spectres de corps noirs à différentes températures
Crédit :
ASM
Spectres stellaires
Cela n'est vrai que pour l'allure du spectre : à plus haute résolution,
il apparaît clairement que se superposent à l'enveloppe du corps noir
des raies en absorption. Si le spectre de corps noir ne dépend que de la
température d'équilibre du corps, les raies signent la présence des
éléments constitutifs de l'atmosphère stellaire.
Le spectre des étoiles chaudes s'écarte significativement de la courbe du corps noir, en raison de l'ionisation de l'hydrogène par des photons de longueur d'onde inférieure à 360 nm.
Spectre stellaire

Spectre stellaire (type G2) à basse résolution. Il se superpose approximativement
à un spectre de corps noir de température 5700 K, sauf dans le domaine UV.
Crédit :
ASM
Spectre stellaire
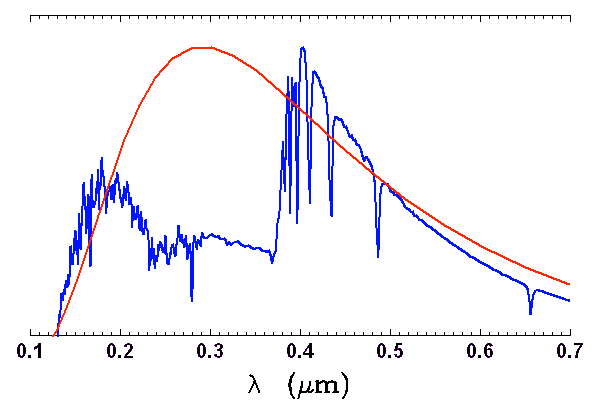
Spectre d'une étoile chaude (type G1) à basse résolution. L'absorption intense en deçà de 360 nm, due à l'ionisation de l'hydrogène, ecarte le spectre de l'enveloppe du corps noir.
Crédit :
ASM
 Objectifs
Objectifs
- Définir le rayonnement du corps noir
- Le corps est finalement une entité physique idéale, dont le rayonnement ne
se caractérise plus que par sa température d'équilibre
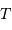
- Les définitions des grandeurs énergétiques utiles sont rappelées à la page de photométrie énergétique.
Courbes de lumière de corps noirs
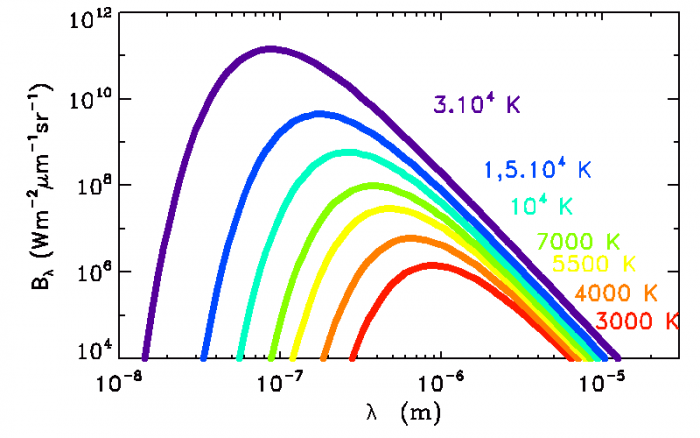
Luminance monochromatique du corps noir, pour des températures
correspondant à divers types stellaires
Crédit :
ASM
Le dénominateur de la loi de Planck est caractéristique d'une loi
statistique de Bose-Einstein, à laquelle obéit un gaz de photons. Comme
tout vecteur d'interaction fondamentale (l'interaction
électromagnétique), le photon est un boson, une particule de spin entier.
La fonction 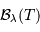 dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non
dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non 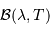 ,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
exercice).
,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
exercice).
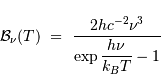
L'unité de 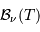 est alors :
est alors :
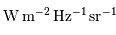 .
.
Courbe de rayonnement
A l'aide de l'appliquette ci-dessous, vous pouvez tracer un spectre de corps noir en fonction de sa température.

 Luminances spectrales
Luminances spectrales
Difficulté : ☆
Temps : 20 min
Question 1)
On considère la luminance du corps noir, dans un domaine spectral de
largeur 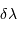 autour de la longueur d'onde
autour de la longueur d'onde 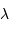 .
Exprimer les fréquence et intervalle de fréquence correspondant.
.
Exprimer les fréquence et intervalle de fréquence correspondant.
La relation entre fréquence et longueur d'onde du rayonnement s'écrit :
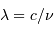
Question 2)
Exprimer la luminance du corps noir de 2 manières
différentes, en fonction de ce qui précède.
La luminance correspond à la luminance spectrale intégrée sur un
intervalle spectral
La conservation de l'énergie conduit à égaler les expressions trouvées
pour la luminance, fonction de 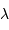 ou
ou 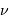 .
.
Rappel
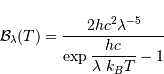
La loi de déplacement de Wien
La représentation de la superposition
de plusieurs spectres de corps noir permet de faire le lien entre la
température du corps noir et la longueur d'onde où a lieu l'émission
maximale. On peut vérifier que les maxima sont simplement
alignés, dans un diagramme en échelle logarithmique.
On en déduit la relation reliant
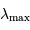 , abscisse du maximum, et la température
, abscisse du maximum, et la température 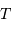 , en
tenant compte de l'échelle logarithmique de la figure :
, en
tenant compte de l'échelle logarithmique de la figure :
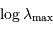 en relation affine avec
en relation affine avec 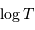 implique
que ces 2 termes sont fonction monomiales l'un de l'autre, en fait
inverse l'un de l'autre.
implique
que ces 2 termes sont fonction monomiales l'un de l'autre, en fait
inverse l'un de l'autre.
Courbes de lumière de corps noirs stellaires
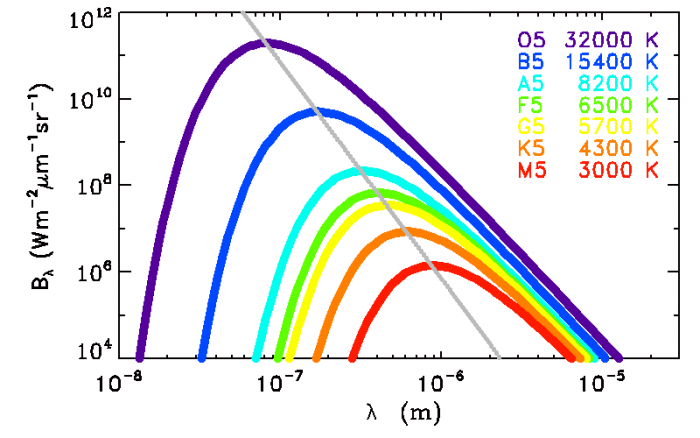
La couleur de chacun des luminances spectrales représentées rappelle
la température de couleur de l'objet. Les maxima s'alignent sur une droite.
Crédit :
ASM
 Objectifs
Objectifs
La loi de déplacement de Wien
Le calcul du maximum d'intensité de la
courbe de luminance
spectrale du corps noir passe par une dérivation de cette fonction.
Sans calcul, la présence au dénominateur, sous l'exponentielle, du
produit 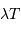 , qui seul introduit la température, implique que la condition d'extremum va être une
fonction de ce produit
, qui seul introduit la température, implique que la condition d'extremum va être une
fonction de ce produit 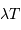 .
.
En notant 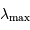 la longueur d'onde du maximum de luminance
spectrale,
il apparaît donc :
la longueur d'onde du maximum de luminance
spectrale,
il apparaît donc :
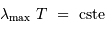
Le calcul de cette constante donne :
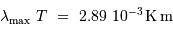
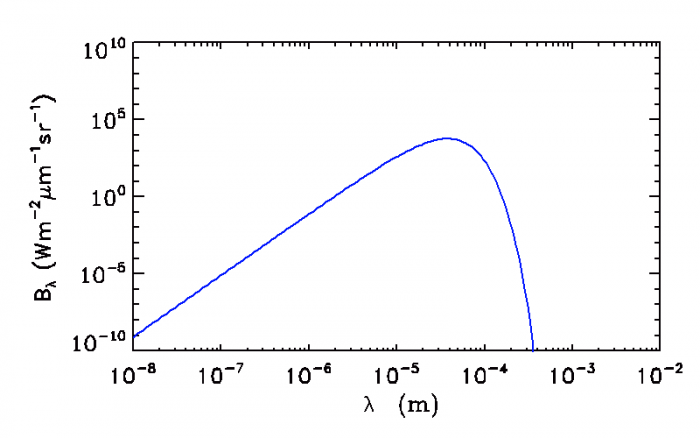
Crédit :
ASM
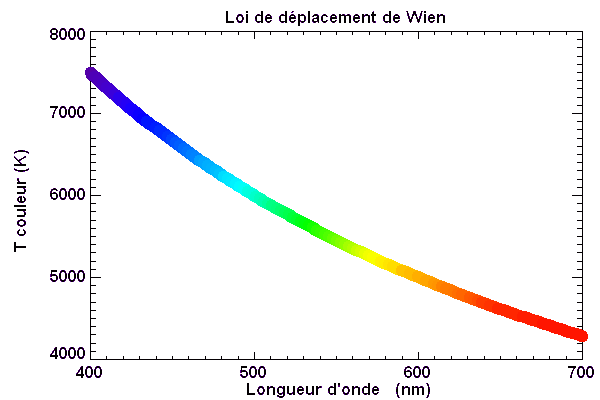
Lien entre température de corps noir et couleur
Crédit :
ASM
Couleur des étoiles
La couleur apparente d'une étoile ne va pas exactement correspondre à la température de son maximum d'émission. En effet, la couleur perçue par le détecteur va intégrer une bonne part de l'énergie rayonnée, et pas seulement celle au maximum d'émission.
Il ne faut pas oublier que la perception des couleurs dépend intimement de la détection : derrière un filtre rose, on voit la vie en rose ! Les couleurs restituées par une image en couleur, obtenue par composition de 3 images dans 3 filtres différents, vont le plus souvent être très vives (pour des raisons esthétiques) que celles vues à l'oeil nu.
On peut néanmoins dégager quelques impressions générales :
- Une étoile de température effective 10000 K, qui rayonne
essentiellement dans le proche UV, apparaîtra blanche, à l'oeil nu, cette impression
résultant de la superposition de toutes les couleurs du spectre.
- Il faut vraiment qu'une étoile soit très froide pour apparaître
rougeâtre. Une étoile froide apparaît plutôt orange.
- IL faut de même qu'une étoile soit très chaude pour apparaître bleutée.
- Une étoile apparaît rarement de couleur tirant sur le vert, ou alors uniquement par contraste avec un objet voisin très rouge (ou bien lorsque le rayonnement n'est pas de type corps noir, mais monochromatique dans une raie d'émission telle celle de l'oxygène, suite à un processus d'excitation qui n'a rien à voir avec le corps noir)
Couleurs

Couleurs dans l'amas NGC6093
Crédit :
HST
Couleurs

Couleurs dans Orion. Les étoiles bleues sont bien plus chaudes que les rouges. Attention, toute couleur ne se traduit pas en température : la nébuleuse d'Orion, M42, doit sa couleur rose à une raie de l'hydrogène.
Crédit :
CFHT
Couleur des étoiles
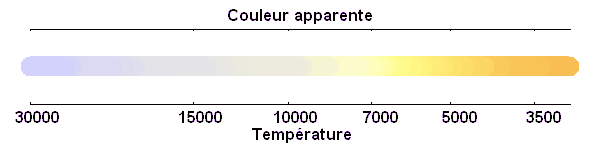
La couleur des étoiles perçue par l'oeil ne correspond pas à ce que détermine leur température via la loi de Wien : l'oeil intègre à sa façon toutes les couleurs présentes dans le spectre visible. La perception des couleurs est très variable d'un individu à l'autre, et souvent subjective.
Crédit :
ASM
 Objectifs
Objectifs
- Définir la température pour un corps assimilable à un
corps noir
 Corps noir ou pas ?
Corps noir ou pas ?
Difficulté : ☆☆
Temps : 5 min
Question 1)
Le pull de votre voisin est jaune, quelle est sa température ?
[1 points]
Question 2)
La question précédente est-elle bien posée ?
[1 points]
Question 3)
Tracer l'allure du spectre de ce pull, à très basse résolution spectrale. Ne pas oublier que votre voisin
en bonne santé a une température corporelle de 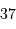 C.
C.
[2 points]
Puissance totale rayonnée
 Objectifs
Objectifs
Etablir le bilan de la puissance rayonnée par un corps noir stellaire.
Quelle puissance rayonne une étoile de température d'équilibre 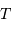 , assimilable à un corps
noir de température
, assimilable à un corps
noir de température 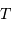 , supposée sphérique de rayon
, supposée sphérique de rayon 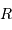 ? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
Le calcul aboutit à la puissance :
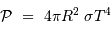
avec la constante de Stefan : 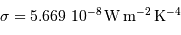 .
.
Puissance totale rayonnée
On peut justifier rapidement la présence des termes 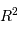 et
et 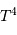 dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
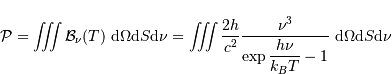
implique, pour la dépendance en fonction du rayon, un terme proportionnel à la surface
stellaire, variant donc comme 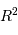 , et pour le terme de température, un
terme proportionnel à
, et pour le terme de température, un
terme proportionnel à 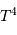 , mis en évidence par le changement de
variable
, mis en évidence par le changement de
variable 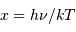 , qui conduit à :
, qui conduit à :
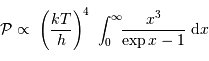
Les termes non explicités dans cette équation ne dépendent pas de la
température, pas plus que l'intégrale sur la variable 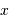 , qui n'est
plus qu'un simple nombre
, qui n'est
plus qu'un simple nombre 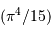 .
.
La loi en 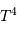 entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leurévolution.
 Rayon stellaire
Rayon stellaire
Difficulté : ☆☆☆
Temps : 45min
La puissance rayonnée par une étoile, assimilée à un corps noir de rayon 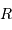 et température
et température 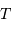 , varie comme :
, varie comme :
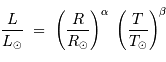
avec 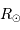 ,
, 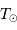 et
et 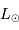 respectivement les rayon, température effective et luminosité du soleil.
respectivement les rayon, température effective et luminosité du soleil.
Question 1)
Rappeler les valeurs de 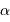 et
et 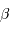
Voir la définition de la puissance rayonnée par un corps noir sphérique de rayon 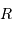 et
de température
et
de température 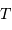
Question 2)
Une naine blanche présente une luminosité 100 fois inférieure à celle du Soleil, pour une température 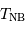 . Estimer son
rayon
. Estimer son
rayon 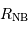 , en fonction des données solaires et de
, en fonction des données solaires et de 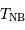 .
.
Il s'agit d'une simple application de la question précédente
Question 4)
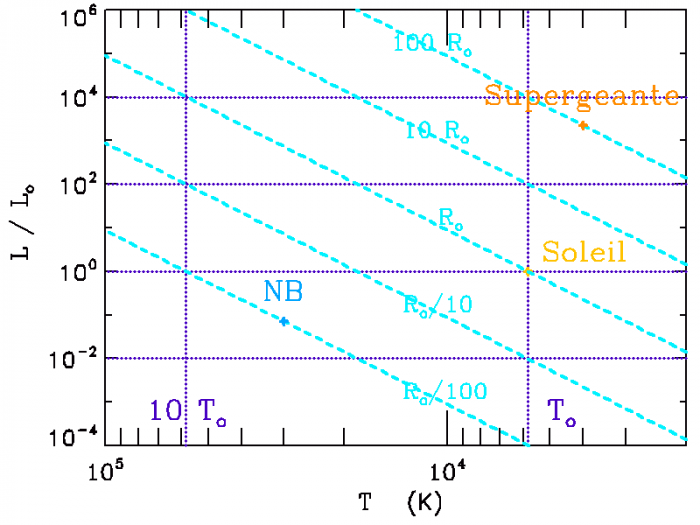
Représenter sur le diagramme ci-joint les lignes iso-rayon, pour les étoiles de respectivement 0.1, 1 et 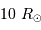 .
.
Diagramme HR
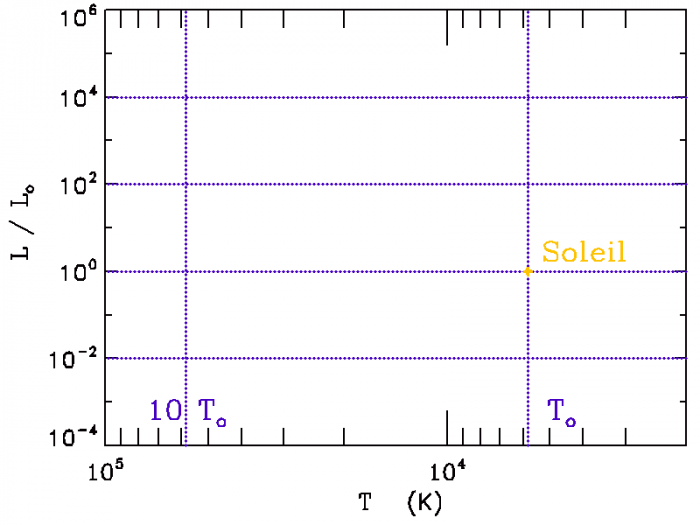
Diagramme HR : température en abscisse, luminosité (par rapport à la luminosité solaire) en ordonnée, avec en pointillé les
lignes iso-luminosité et iso-température (pour les températures
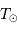
et
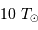
)
Crédit :
ASM
Le diagramme est en échelle log-log. Plutôt que de représenter les valeurs de température 1000, 10000 K par les logarithmes décimaux 3 et 4
selon une échelle linéaire, il présente 1000 et 10000 en échelle logarithmique.
Avec une telle échelle, une loi de puissance 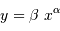 se traduit linéairement par
se traduit linéairement par
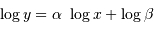
Une ligne iso-rayon relie dans le diagramme des étoiles de températures et luminosités variables, mais rayons identiques.
Question 5)
Situer sur ce diagramme une supergéante rouge de rayon 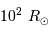 et une naine blanche de rayon
et une naine blanche de rayon 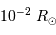 , de
température respective 4000 et 30 000 K.
, de
température respective 4000 et 30 000 K.
 Mesure de la température effective
Mesure de la température effective
Difficulté : ☆
Temps : 20 min
La loi de Stefan permet de calculer la température d'un corps noir à partir de sa luminosité et de sa taille. La difficulté est que ces deux termes dépendent de la distance de l'objet. L'exercice se propose de voir comment pallier cette difficulté, dès lors que l'on peut connaître, par interférométrie, le rayon angulaire de l'étoile. Par la suite, on note 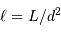 le flux relatif de l'étoile et
le flux relatif de l'étoile et 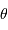 le rayon angulaire de l'étoile.
le rayon angulaire de l'étoile.
Question 1)
Comment 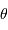 s'exprime-t-il en fonction du rayon
s'exprime-t-il en fonction du rayon 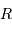 et de la distance
et de la distance 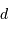 ?
?
[1 points]
L'approximation des petits angles est amplement justifiée.
Question 2)
Réécrire la relation de luminosité du corps noir en fonction des observables 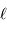 et
et 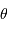 . En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
. En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
[2 points]
 Objectifs
Objectifs
Le corps correspond à un équilibre entre un corps de température 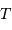 et un rayonnement de corps noir à cette même température.
et un rayonnement de corps noir à cette même température.
Thermalisation
L'exemple du soleil
permet de définir la température effective d'un corps noir, ou
température d'équilibre, ou température de brillance.
Le parcours de l'énergie au sein du soleil est, jusqu'aux couches
supérieures, une succession ininterrompue d'absorption et de réémission des photons initialement produits par les réactions nucléaires au centre de l'étoile, dans le domaine 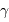 , jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
, jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
Arrivés dans la photosphère, les photons peuvent quitter le soleil, avec une distribution énergétique qui est celle du corps noir, de température donnée, que l'on appelle température effective.
Equilibre
En raison de l'équilibre entre le rayonnement de corps noir et la matière
du corps noir, il y a concordance entre cette température et celle du milieu
émetteur. D'après le second principe de la thermodynamique, les
couches atmosphériques plus profondes qui ont fourni l'énergie ne
peuvent être qu'à une température plus élevée. Il s'ensuit un certain
nombre de conséquences :
- La température effective correspond à la
température minimale rencontrée dans la partie supérieure de l'atmosphère
stellaire
- Le niveau de l'atmosphère que l'on voit, par définition celui dont sont
issus les photons, est de température très voisine à la température effective.
- Les niveaux inférieurs sont opaques, vu que le processus de
thermalisation entre matière et rayonnement y est à l'oeuvre
 Equilibre thermique d'une planète
Equilibre thermique d'une planète
Difficulté : ☆☆
Temps : 60 min
On s'intéresse au bilan radiatif d'une planète en orbite circulaire de rayon 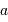 autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température
autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température 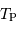 comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
La planète réfléchit une fraction 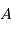 du rayonnement solaire, et en
absorbe une fraction
du rayonnement solaire, et en
absorbe une fraction 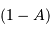 , où
, où 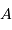 est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note
est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note 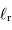 la composante énergétique directement
réfléchie, et
la composante énergétique directement
réfléchie, et 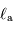 la composante absorbée puis rerayonnée.
la composante absorbée puis rerayonnée.
Question 1)
Montrer que la puissance interceptée par la planète vaut :
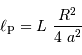
où 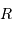 représente le rayon planétaire.
représente le rayon planétaire.
Faire un schéma, et estimer la surface interceptée par la planète
Question 2)
Calculer le rapport 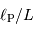 dans le cas de Jupiter et de la Terre.
dans le cas de Jupiter et de la Terre.
| Objet | 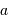 (UA) (UA) | 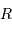 (km) (km) |
| Jupiter | 5.2 | 71000 |
| Terre | 1 | 6400 |
Pour mémoire 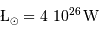 .
.
Question 4)
Quelle est la température 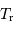 associée au rayonnement réfléchi
associée au rayonnement réfléchi 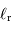 , assimilé à un rayonnement de corps noir ?
, assimilé à un rayonnement de corps noir ?
Question 5)
Montrer que la température associée à la composante
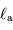 , voisine de la température d'équilibre de la planète, est alors:
, voisine de la température d'équilibre de la planète, est alors:
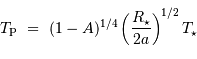
Associer 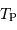 au rayonnement de type corps noir
au rayonnement de type corps noir 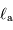 .
.
Question 7)
En déduire la longueur d'onde 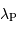 correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
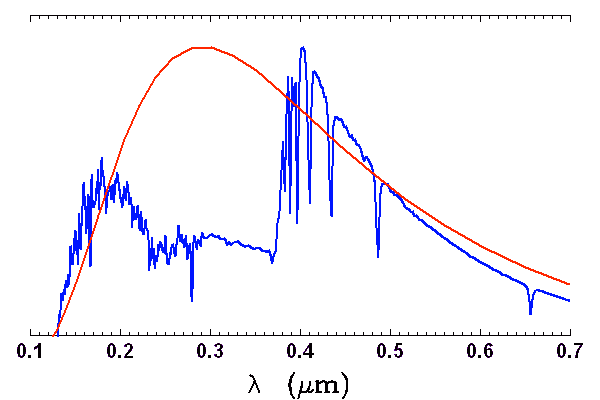
Raie de Balmer de l'hydrogène superposées au spectre stellaire visible d'une étoile chaude de type A.
Crédit :
ASM
Spectres stellaires
Un spectre stellaire présente, superposées à un spectre continu de type corps noir, des raies en absorption. Leur présence conduit à répartir l'énergie différemment du spectre du corps noir, dont on retrouve néanmoins la trace dans l'allure générale du spectre à basse résolution.

Le spectre du corps noir est insuffisant pour rendre compte de l'aspect de Jupiter à ces différentes longueurs d'onde, mais fournit une explication pour les variations de la magnitude moyenne. C'est à 3.40 micromètres, minimum de luminosité entre le spectre solaire réfléchi et le spectre du corps noir jovien, que Jupiter apparaît le plus sombre.
Crédit :
NASA
Raies et continu
La plupart des spectres des objets astrophysiques résultent de la somme des contributions spectrales superposées au corps noir. Sur la mosaïque d'images infrarouges de Jupiter ci-jointe, contributions spectrales et de corps noir s'entremêlent.
À 1.60 micromètres, le rayonnement de corps noir (le spectre solaire réfléchi) domine.
À 3.41 micromètres, minimum entre les corps noirs jovien et solaire réfléchi, la contribution prépondérante provient de l'émission stratosphérique de l'ion 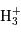 . À plus haute longueur d'onde, le spectre de corps noir de Jupiter prend de l'importance, et révèle les inhomogénéités de la troposphère jovienne.
. À plus haute longueur d'onde, le spectre de corps noir de Jupiter prend de l'importance, et révèle les inhomogénéités de la troposphère jovienne.
Spectres stellaires
Un spectre stellaire présente, superposé à un spectre continu de type corps noir, des raies en absorption.
La température d'équilibre correspond à la température de la photosphère, d'où s'échappent les photons, qui correspond à un minimum local de température.
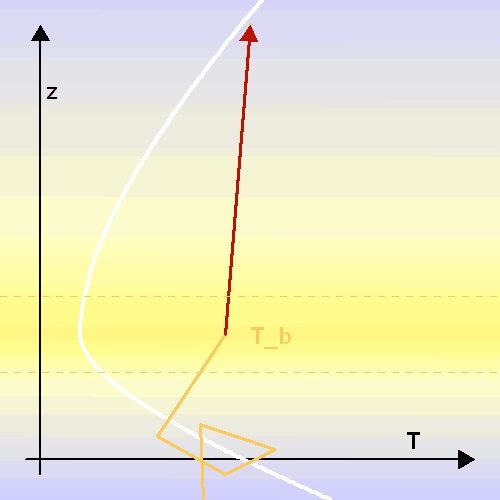
La température d'équilibre correspond à la température de la photosphère, d'où s'échappent les photons.
Crédit :
ASM
Spectres planétaires
Un spectre planétaire présente, superposé à un spectre continu de type corps noir, des raies en absorption ou en émission. Contrairement à un spectre stellaire, le spectre planétaire voit 2 sources chaudes : son étoile et sa structure interne.
Le minimum de température correspond à la tropopause.
Les raies en absorption signalent un déficit énergétique par rapport au corps noir, et signent la présence d'un absorbant dans la troposphère : région où la température décroît avec l'altitude. Cet élément a ponctionné une partie de l'énergie dans la raie considérée. Dans cette région plus profonde que la tropopause, l'énergie est redistribuée à toute longueur d'onde, suite aux multiples interaction matière-rayonnement.
Les raies en émission signalent un surcroît énergétique par rapport au corps noir, et signent la présence d'un absorbant dans la stratosphère : région où la température croît avec l'altitude. Cet élément a ponctionné une partie de l'énergie solaire incidente dans la raie considérée, et la réémet.
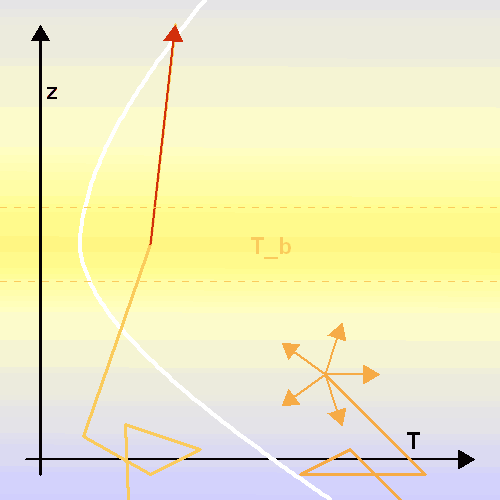
Les raies en absorption proviennent de la troposphère.
Crédit :
ASM
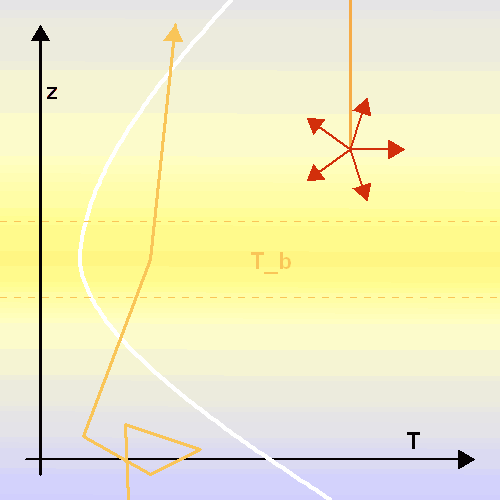
Les raies en émission proviennent de la stratosphère.
Crédit :
ASM
Fond cosmologique
L'observation spectroscopique du rayonnement du fond cosmologique met en
évidence un rayonnement de corps noir, le corps noir cosmologique. Sa température
d'équilibre est de l'ordre de 3 K (2.728 K pour être très précis).
La loi de déplacement de Wien associe cette température à un maximum
d'émission dans les longueurs d'onde millimétrique.
Le corps noir cosmologique
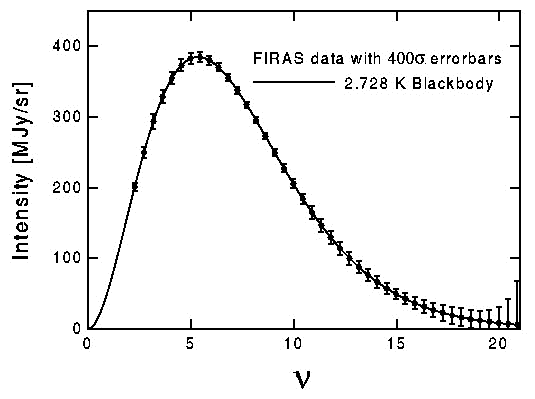
Le spectre du rayonnement du fond cosmologique est de type corps noir. Mesure de l'instrument FIRAS du satellite CoBE (Cosmic Background Explorer) de la NASA.
L'échelle spectrale est donnée en fréquence (unité =
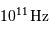
).
Crédit :
NASA
Spectre planétaire
L'allure d'un spectre
planétaire montre une courbe "à 2 bosses". Les 2 maximas locaux
piquent à 0.5 et 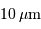 , soit à des températures effectives
de 6000 et 300 K approximativement.
, soit à des températures effectives
de 6000 et 300 K approximativement.
Les 2 contributions du spectre ont clairement 2 origines distinctes :
- La composante visible correspond à la réflexion du spectre
stellaire réfléchi par la planète
- La composante infrarouge rend compte du spectre de corps noir
planétaire. La planète est à l'équilibre thermique entre 2 sources :
l'apport énergétique de l'étoile (source chaude), et le rayonnement vers le ciel (source
froide).
Spectre planétaire, à basse résolution
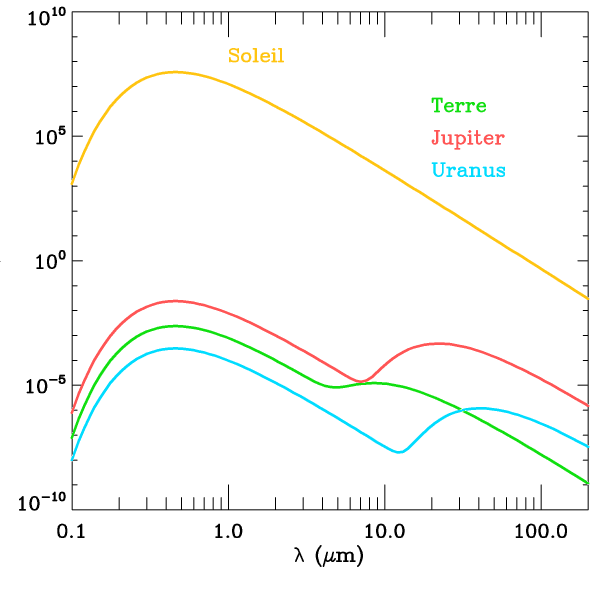
Deux composantes de type corps noir constituent le rayonnement des spectres planétaires à basse résolution spectrale : le spectre solaire réfléchi, et le spectre thermique.
Crédit :
ASM
Fond cosmologique
Dans le cadre de la théorie du big-bang, l'Univers est en expansion et se refroidit. Il est passé dans le passé par des phases plus chaudes, et a connu diverses étapes, correspondant à des ruptures d'équilibre.
Pour des température de plus 3000 K, la matière et le rayonnement était à l'équilibre, suite à l'interaction entre les électrons, libres, et les photons. Aux températures plus faibles, la recombinaison des électrons avec les protons pour former l'hydrogène atomique a occasionné le découplage de la matière et du rayonnement.
Ce dernier garde une distribution énergétique de corps noir, mais s'est refroidi suite à l'expansion de l'univers.
Il présente aujourd'hui une température, très homogène, de 2.728 K.
Spectres planétaires
En première approximation, on peut distinguer 2 composantes dans un spectre planétaire :
- Le spectre solaire directement réfléchi
- Le spectre infrarouge, rayonnée par la planète en fonction de sa température d'équilibre
Stricto sensu, le rayonnement n'est plus un rayonnement de corps noir. En fait, les 2 composantes sont proches de 2 corps noirs, l'un à la température du rayonnement stellaire, l'autre à la température d'équilibre planétaire.
Spectre planétaire, à basse résolution
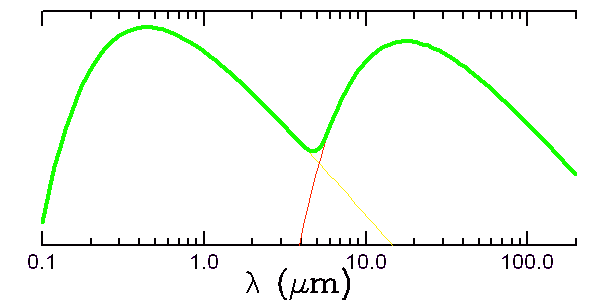
Deux composantes de type corps noir constituent le rayonnement d'un spectre planétaire
observé à basse résolution spectrale.
Crédit :
ASM
 Température d'antenne
Température d'antenne
Difficulté : ☆☆☆
Temps : 45 min
Il a été vu que la luminance
spectrale du corps noir s'exprime,
en fonction de la fréquence
par :
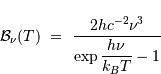
Dans cet exercice, on se propose de montrer comment cela conduit les
radio-astronomes à exprimer une luminosité radio comme une température, et donc
à l'exprimer en Kelvin.
Les conditions d'observation de l'image, définies par la
diffraction, énoncent
que le faisceau élémentaire observable a une étendue 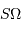 égale à
égale à 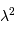 , et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur
, et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur 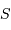 et sur
et sur 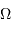 permet de passer de la luminance spectrale à la puissance spectrale.
permet de passer de la luminance spectrale à la puissance spectrale.
La surface 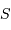 représente ici la
surface collectrice, et
représente ici la
surface collectrice, et 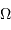 l'angle solide sous lequel est vue la
source élémentaire.
l'angle solide sous lequel est vue la
source élémentaire.
Question 1)
Montrer que, dans le domaine des radiofréquences, la fréquence
d'observation 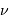 , typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
, typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
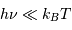
On donne 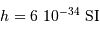 , et
, et 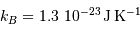 .
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
.
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
Ce n'est qu'une application numérique !
Question 2)
En déduire l'approximation de la loi de rayonnement dans le domaine
radio :
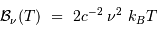
On rappelle le développement limité : 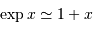 , pour
, pour 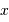 petit.
petit.
Question 3)
Montrer que l'intégration de la luminance spectrale 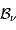 , vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
puissance égale à
, vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
puissance égale à
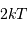
Faire le lien entre les termes de l'étendue de faisceau et les termes
énergétiques.
Question 4)
Déterminer alors la puissance reçue dans l'intervalle de fréquence
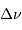 .
.
Il ne reste plus qu'à intégrer sur l'intervalle spectral, sans oublier
qu'une seule des deux polarisations est visible.
 Spectre d'une exoplanète
Spectre d'une exoplanète
Difficulté : ☆☆
Temps : 10 min
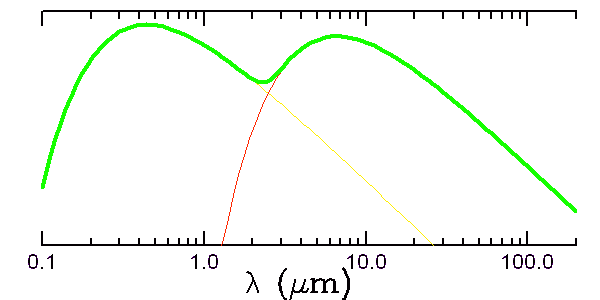
Spectre exoplanétaire simulé à basse résolution spectrale.
Crédit :
ASM
Question 1)
Interpréter la figure ci-jointe, simulant un spectre exoplanétaire.
[1 points]
Question 2)
Estimer les températures effectives associées à ce spectre.
[2 points]
Question 3)
Cette planète est supposée de type tellurique, de rayon égal à celui de
la Terre et située à 1 UA de son étoile, laquelle est de type à peu près
solaire. Comparer sa température d'équilibre à celle de la Terre.
Subit-elle un effet de serre important ?
[1 points]
L'application des lois concernant le corps (loi du rayonnement, loi de Wien, loi de Planck) est très souvent féconde... mais il faut tout d'abord retenir de ces pages les conditions physiques dans lesquelles peut s'appliquer le modèle du corps noir : le rayonnement doit traduire l'équilibre thermique de l'objet considéré. Sans cette hypothèse, l'application des lois précédentes reste vaine, et peut conduire à de gros contresens (que l'on retrouve souvent dans la littérature, lorsque la notion de température de couleur est utilisée tellement loin de son domaine de validité qu'elle en perd tout son sens).
En première approximation, les étoiles rayonnent comme des corps noirs... mais les nombreuses raies d'absorption peuvent conduire à un profil de rayonnement bien déformé. Le rayonnement du fond cosmologique est quant à lui un excellent corps noir.

Corps noir volatile certes, mais corps noir physique ?
Crédit :
ASM
- Question 1
Aide :
La relation entre fréquence et longueur d'onde du rayonnement s'écrit :
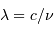
Aide :
La relation entre 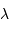 et
et 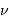 donne celle entre les intervalles
spectraux
donne celle entre les intervalles
spectraux 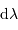 et
et 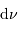 , par différentiation.
, par différentiation.
Solution :
La relation entre fréquence et longueur d'onde du rayonnement s'exprime
: 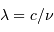 . On en déduit :
. On en déduit :
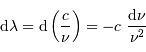
Le signe négatif rappelle que les
échelles en longueur d'onde et fréquence sont inversées. Par la suite,
avec une définition adéquate des bornes de l'intervalle, on écrit :
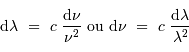
- Question 2
Aide :
La luminance correspond à la luminance spectrale intégrée sur un
intervalle spectral
Aide :
La conservation de l'énergie conduit à égaler les expressions trouvées
pour la luminance, fonction de 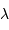 ou
ou 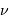 .
.
Aide :
Rappel
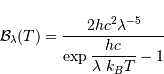
Solution :
La luminance, intégrée sur l'intervalle spectral,
s'écrit donc de 2 façons différentes, qui doivent rendre compte de la
même énergie dans l'intervalle spectral considéré :
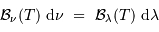
d'où
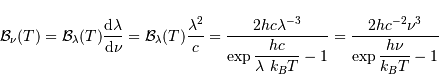
La correspondance est établie.
- Question 1
Aide :
Voir la définition de la puissance rayonnée par un corps noir sphérique de rayon 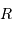 et
de température
et
de température 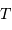
Solution :
La puissance du corps noir étant proportionnelle à 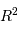 et
et 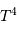 , il sort simplement :
, il sort simplement :
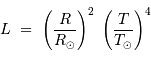
- Question 2
Aide :
Il s'agit d'une simple application de la question précédente
Solution :
L'égalité des luminosités se traduit par :
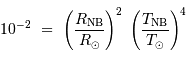
On en déduit :
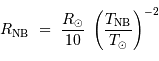
- Question 3
Solution :
L'application numérique de la question précédente donne
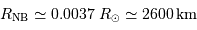
- Question 4
Aide :
Le diagramme est en échelle log-log. Plutôt que de représenter les valeurs de température 1000, 10000 K par les logarithmes décimaux 3 et 4
selon une échelle linéaire, il présente 1000 et 10000 en échelle logarithmique.
Avec une telle échelle, une loi de puissance 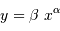 se traduit linéairement par
se traduit linéairement par
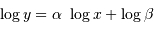
Aide :
Une ligne iso-rayon relie dans le diagramme des étoiles de températures et luminosités variables, mais rayons identiques.
Solution :
On s'intéresse à la ligne iso-rayon de rayon solaire. Elle est caractérisée par l'équation reliant température et luminosité s'exprimant :
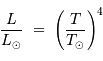
L'exposant 4 se traduit par une pente de 4 dans le diagramme log-log. La droite de pente 4 relie par exemple les points
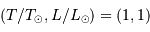 et
et 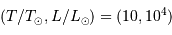 . Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.
. Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.
Diagramme HR
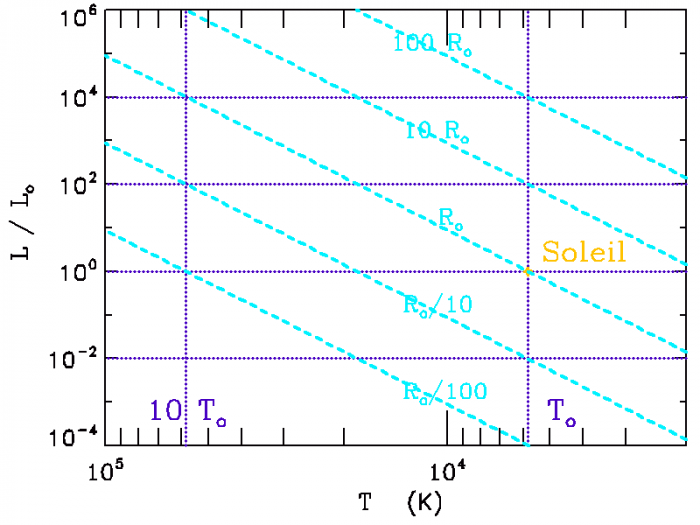
Diagramme HR avec lignes iso-rayon
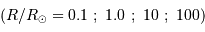
Crédit :
ASM
- Question 5
Solution :
L'application de l'expression donnant la luminosité
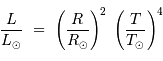
conduit, pour la géante rouge, à :
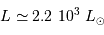
et pour la naine blanche :
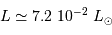
Diagramme HR
Crédit :
ASM
- Question 1
Aide :
Faire un schéma, et estimer la surface interceptée par la planète
Solution :
Au niveau de la planète, le flux stellaire est dilué sur une sphère de surface
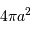 .
La section occultée par la planète, avec
.
La section occultée par la planète, avec 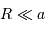 , correspond à celle d'un disque de surface
, correspond à celle d'un disque de surface 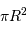 .
.
Le rapport de ces 2 aires vaut :
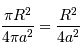
d'où le résultat proposé.
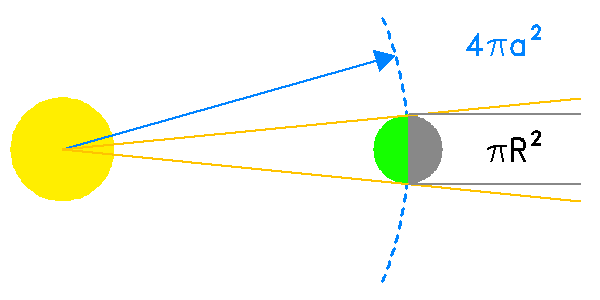
Avec l'hypothèse
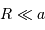
, la surface interceptée par la planète est voisine de
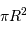
.
Crédit :
ASM
- Question 2
Aide :
Calculette !
Solution :
Les applications numériques donnent :
| Objet | 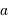 (UA) (UA) | 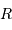 (km) (km) | 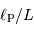 |
| Jupiter | 5.2 | 71000 | 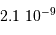 |
| Terre | 1 | 6400 | 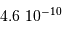 |
- Question 3
Aide :
L'énergie se conserve !
Solution :
La conservation de l'énergie impose
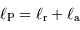
Toute l'énergie reçue sera rerayonnée, soit directement, soit après thermalisation. D'après la définition de l'albédo, il s'ensuit le partage :
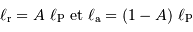
- Question 4
Aide :
Aucun calcul à mener !
Solution :
Le rayonnement directement réfléchi correspond au rayonnement solaire. Sa température de corps noir est donc 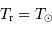 .
.
- Question 5
Aide :
Associer 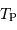 au rayonnement de type corps noir
au rayonnement de type corps noir 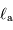 .
.
Solution :
Le rayonnement thermique de la planète correspond, par hypothèse, à un rayonnement de corps noir de température 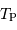 .
.
Il vérifie :
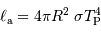
Par ailleurs :
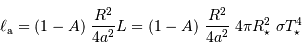
On en déduit :
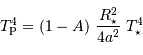
D'où le résultat à démontrer :
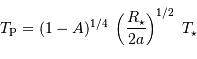
- Question 6
Aide :
Re-calculette !
Solution :
L'application numérique donne environ 1000 K.
- Question 7
Aide :
Aller voir la loi de Wien
Solution :
La loi de Wien donne :
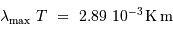
On en déduit que le maximum de rayonnement se situe aux alentours de 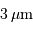 .
.
- Question 1
Aide :
Ce n'est qu'une application numérique !
Solution :
L'énergie thermique est :
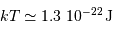
L'énergie d'un photon vaut 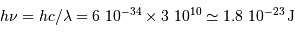 .
.
L'inégalité stricte demandée est bien vérifiée.
- Question 2
Aide :
On rappelle le développement limité : 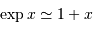 , pour
, pour 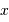 petit.
petit.
Solution :
Avec l'approximation 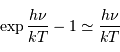 , valide vu l'hypothèse posée, on trouve :
, valide vu l'hypothèse posée, on trouve :
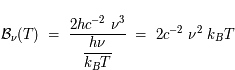
- Question 3
Aide :
Faire le lien entre les termes de l'étendue de faisceau et les termes
énergétiques.
Aide :
Intégrer simultanément la densité spectrale de luminance sur la surface collectrice
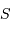 , et sur tout l'angle solide
, et sur tout l'angle solide 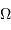 , avec la propriété admise :
, avec la propriété admise :
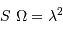 .
.
Solution :
La densité spectrale de luminance vaut :
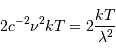
Intégrée sur la variable de surface 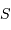 et celle d'angle solide
et celle d'angle solide 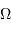 , on trouve, avec
, on trouve, avec 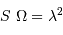 , une puissance monochromatique :
, une puissance monochromatique :
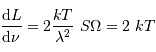
- Question 4
Aide :
Il ne reste plus qu'à intégrer sur l'intervalle spectral, sans oublier
qu'une seule des deux polarisations est visible.
Solution :
L'antenne n'est sensible qu'à une seule direction du champ électrique :
la moitié de l'énergie est donc perdue. En supposant la densité
spectrale de puissance uniforme sur l'intervalle de fréquence, on trouve
une puissance :
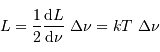
Cette valeur apparaît directement proportionnelle à la largeur de
l'intervalle spectral, fixée par la détection, et à la température de la
source.
C'est pourquoi les radioastronomes définissent la puissance
reçue par une température.
Cette température correspond directement à celle du corps s'il rayonne
comme un corps noir. Mais, toute énergie devenant ainsi une température
(température de bruit du
détecteur, ou de température d'antenne) par une simple règle de
proportionnalité, cette température ne peut pas être considérée, dans la
plupart des cas, comme une température thermodynamique.








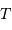
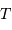 :
:
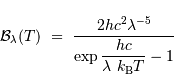
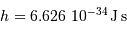 , la constante de Boltzmann
, la constante de Boltzmann 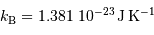 , et
, et 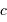 la célérité de la lumière dans le vide. Ceci indique que la loi de Planck est à l'intersection, respectivement, de la physique quantique, statistique et relativiste.
la célérité de la lumière dans le vide. Ceci indique que la loi de Planck est à l'intersection, respectivement, de la physique quantique, statistique et relativiste.
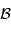 s'exprime en
s'exprime en 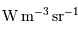 , ou en unité
dérivée
, ou en unité
dérivée 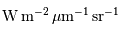 ;
; 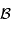 est une
est une

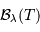 dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non
dépend de la température comme de la
longueur d'onde. Elle est notée ainsi, et non 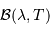 ,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
,
pour mettre en évidence la variable spectrale, ici la longueur d'onde.
Cette dépendance spectrale peut également s'exprimer en fonction non de la
longueur d'onde, mais de la fréquence. La loi de Planck se réécrit alors
dans ce cas (justification donnée en
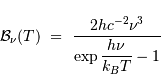
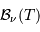 est alors :
est alors :
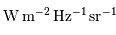 .
.

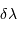 autour de la longueur d'onde
autour de la longueur d'onde 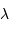 .
Exprimer les fréquence et intervalle de fréquence correspondant.
.
Exprimer les fréquence et intervalle de fréquence correspondant.
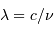
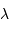 et
et 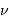 donne celle entre les intervalles
spectraux
donne celle entre les intervalles
spectraux 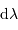 et
et 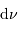 , par différentiation.
, par différentiation.
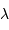 ou
ou 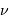 .
.
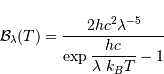
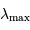 , abscisse du maximum, et la température
, abscisse du maximum, et la température 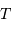 , en
tenant compte de l'échelle logarithmique de la figure :
, en
tenant compte de l'échelle logarithmique de la figure :
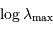 en relation affine avec
en relation affine avec 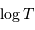 implique
que ces 2 termes sont fonction monomiales l'un de l'autre, en fait
inverse l'un de l'autre.
implique
que ces 2 termes sont fonction monomiales l'un de l'autre, en fait
inverse l'un de l'autre.

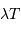 , qui seul introduit la température, implique que la condition d'extremum va être une
fonction de ce produit
, qui seul introduit la température, implique que la condition d'extremum va être une
fonction de ce produit 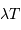 .
.
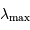 la longueur d'onde du maximum de luminance
spectrale,
il apparaît donc :
la longueur d'onde du maximum de luminance
spectrale,
il apparaît donc :
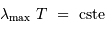
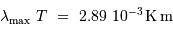
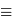 corps noir)
corps noir) 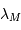
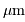
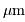
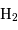
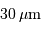 a une température de :
a une température de :





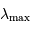 et une couleur.
et une couleur.
 corps noir)
corps noir) 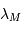
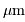
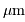
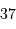 C.
C.
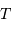 , assimilable à un corps
noir de température
, assimilable à un corps
noir de température 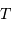 , supposée sphérique de rayon
, supposée sphérique de rayon 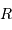 ? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
? La réponse
nécessite d'intégrer la luminance spectrale du corps noir sur toute sa
surface, dans toutes les directions, à toute longueur d'onde.
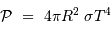
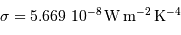 .
.
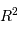 et
et 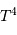 dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
dans cette puissance totale rayonnée.
En effet, l'intégration de la luminance spectrale, spatiale, angulaire et spectrale :
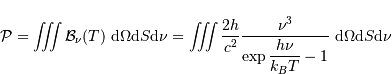
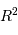 , et pour le terme de température, un
terme proportionnel à
, et pour le terme de température, un
terme proportionnel à 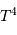 , mis en évidence par le changement de
variable
, mis en évidence par le changement de
variable 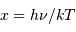 , qui conduit à :
, qui conduit à :
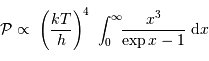
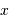 , qui n'est
plus qu'un simple nombre
, qui n'est
plus qu'un simple nombre 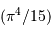 .
.
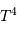 entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leur
entraîne une grande diversité dans la vie des étoiles.
Deux étoiles de rayons analogues mais avec des températures variant du simple au
quintuple (4000 - 20000 K p.ex.) vont avoir des luminosités dans un rapport de
625, donc déjà des couleurs et luminosités très différents. Mais il s'ensuit
également des conséquences très fortes sur leur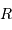 et température
et température 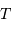 , varie comme :
, varie comme :
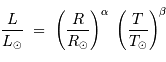
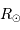 ,
, 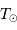 et
et 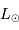 respectivement les rayon, température effective et luminosité du soleil.
respectivement les rayon, température effective et luminosité du soleil.
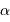 et
et 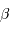
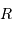 et
de température
et
de température 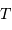
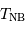 . Estimer son
rayon
. Estimer son
rayon 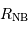 , en fonction des données solaires et de
, en fonction des données solaires et de 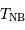 .
.
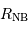 pour
pour 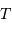 = 30000 K,
= 30000 K, 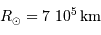 et
et 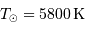 .
.
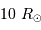 .
.

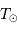 et
et 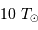 )
)
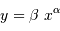 se traduit linéairement par
se traduit linéairement par
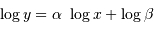
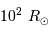 et une naine blanche de rayon
et une naine blanche de rayon 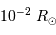 , de
température respective 4000 et 30 000 K.
, de
température respective 4000 et 30 000 K.
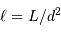 le flux relatif de l'étoile et
le flux relatif de l'étoile et 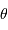 le rayon angulaire de l'étoile.
le rayon angulaire de l'étoile.
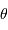 s'exprime-t-il en fonction du rayon
s'exprime-t-il en fonction du rayon 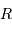 et de la distance
et de la distance 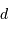 ?
?
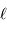 et
et 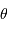 . En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
. En déduire que l'on peut relier la température de corps noir à des grandeurs directement mesurables.
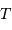 et un rayonnement de corps noir à cette même température.
et un rayonnement de corps noir à cette même température.
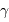 , jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
, jusqu'aux photons finalement émis, majoritairement dans les domaines UV, visible et IR.
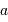 autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température
autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température 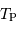 comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
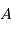 du rayonnement solaire, et en
absorbe une fraction
du rayonnement solaire, et en
absorbe une fraction 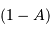 , où
, où 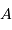 est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note
est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note 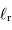 la composante énergétique directement
réfléchie, et
la composante énergétique directement
réfléchie, et 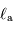 la composante absorbée puis rerayonnée.
la composante absorbée puis rerayonnée.
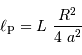
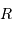 représente le rayon planétaire.
représente le rayon planétaire.
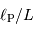 dans le cas de Jupiter et de la Terre.
dans le cas de Jupiter et de la Terre.
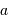 (UA)
(UA) 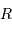 (km)
(km)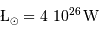 .
.
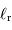 et
et 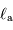 en fonction de la luminosité totale
en fonction de la luminosité totale
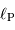 et de l'albédo
et de l'albédo 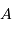 .
.
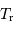 associée au rayonnement réfléchi
associée au rayonnement réfléchi 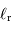 , assimilé à un rayonnement de corps noir ?
, assimilé à un rayonnement de corps noir ?
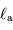 , voisine de la température d'équilibre de la planète, est alors:
, voisine de la température d'équilibre de la planète, est alors:
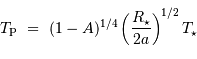
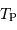 au rayonnement de type corps noir
au rayonnement de type corps noir 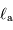 .
.
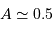 et un demi-grand axe
et un demi-grand axe
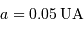 . Pour l'étoile, on prendra :
. Pour l'étoile, on prendra : 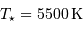 et
et 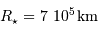 .
.
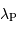 correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?
correspondant au maximum de l'émission planétaire.
A quel domaine spectral cette température correspond-elle?


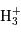 . À plus haute longueur d'onde, le spectre de corps noir de Jupiter prend de l'importance, et révèle les inhomogénéités de la troposphère jovienne.
. À plus haute longueur d'onde, le spectre de corps noir de Jupiter prend de l'importance, et révèle les inhomogénéités de la troposphère jovienne.




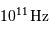 ).
).
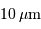 , soit à des températures effectives
de 6000 et 300 K approximativement.
, soit à des températures effectives
de 6000 et 300 K approximativement.


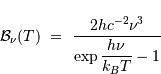
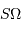 égale à
égale à 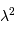 , et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur
, et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur 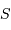 et sur
et sur 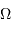 permet de passer de la luminance spectrale à la puissance spectrale.
permet de passer de la luminance spectrale à la puissance spectrale.
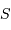 représente ici la
surface collectrice, et
représente ici la
surface collectrice, et 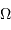 l'angle solide sous lequel est vue la
source élémentaire.
l'angle solide sous lequel est vue la
source élémentaire.
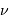 , typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
, typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
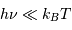
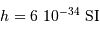 , et
, et 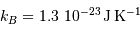 .
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
.
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
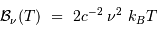
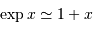 , pour
, pour 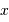 petit.
petit.
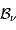 , vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
, vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
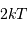
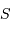 , et sur tout l'angle solide
, et sur tout l'angle solide 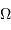 , avec la propriété admise :
, avec la propriété admise :
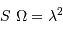 .
.
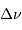 .
.


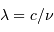 . On en déduit :
. On en déduit :
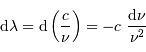
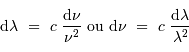
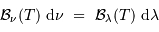
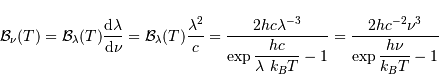
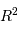 et
et 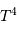 , il sort simplement :
, il sort simplement :
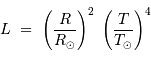
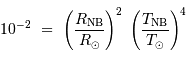
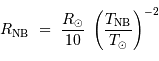
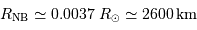
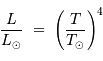
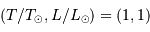 et
et 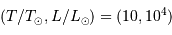 . Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.
. Attention : la pente apparaît négative car l'axe des températures est orienté vers la gauche dans le diagramme HR usuel.

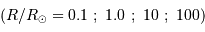
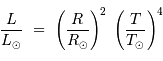
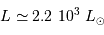
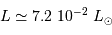

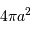 .
La section occultée par la planète, avec
.
La section occultée par la planète, avec 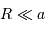 , correspond à celle d'un disque de surface
, correspond à celle d'un disque de surface 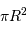 .
.
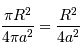

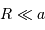 , la surface interceptée par la planète est voisine de
, la surface interceptée par la planète est voisine de 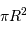 .
.
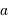 (UA)
(UA) 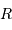 (km)
(km)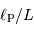
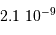
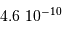
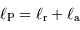
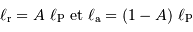
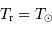 .
.
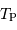 .
.
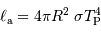
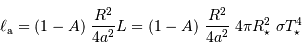
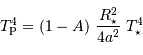
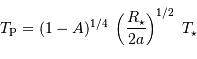
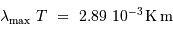
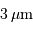 .
.
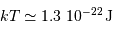
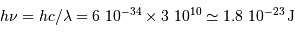 .
.
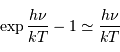 , valide vu l'hypothèse posée, on trouve :
, valide vu l'hypothèse posée, on trouve :
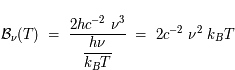
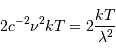
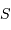 et celle d'angle solide
et celle d'angle solide 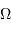 , on trouve, avec
, on trouve, avec 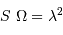 , une puissance monochromatique :
, une puissance monochromatique :