|
Difficulté : ☆☆☆ Temps : 45 min
Il a été vu que la luminance spectrale du corps noir s'exprime, en fonction de la fréquence par :
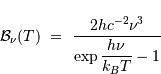
Dans cet exercice, on se propose de montrer comment cela conduit les radio-astronomes à exprimer une luminosité radio comme une température, et donc à l'exprimer en Kelvin.
Les conditions d'observation de l'image, définies par la
diffraction, énoncent
que le faisceau élémentaire observable a une étendue 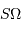 égale à
égale à 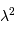 , et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur
, et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur 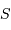 et sur
et sur 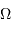 permet de passer de la luminance spectrale à la puissance spectrale.
permet de passer de la luminance spectrale à la puissance spectrale.
La surface 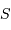 représente ici la
surface collectrice, et
représente ici la
surface collectrice, et 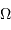 l'angle solide sous lequel est vue la
source élémentaire.
l'angle solide sous lequel est vue la
source élémentaire.
Montrer que, dans le domaine des radiofréquences, la fréquence
d'observation 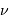 , typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
, typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
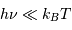
On donne 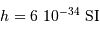 , et
, et 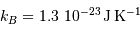 .
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
.
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
En déduire l'approximation de la loi de rayonnement dans le domaine radio :
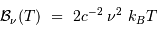
Montrer que l'intégration de la luminance spectrale 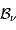 , vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
puissance égale à
, vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
puissance égale à