Caractéristiques des cônes d'ombre et de pénombre

Comme nous l'avons déjà vu la distance entre le centre de la Terre et le sommet du cône d'ombre et donc sa largeur varie en fonction de la distance Terre-Soleil. Elle vaut environ 231 rayons terrestres lorsque la Terre est à l'aphélie et elle vaut 221 rayons terrestres lorsque la Terre est à son périhélie.

De même la distance entre le sommet du cône de pénombre et le centre de la Terre dépend de la distance Terre-Soleil, elle est maximale, environ 216 rayons terrestres lorsque la Terre est à son aphélie et elle est minimale, environ 209 rayons terrestres lorsque la Terre est à son périhélie.

Demi-diamètres apparents géocentriques de l'ombre et de la pénombre

Crédit : IMCCE/Patrick Rocher

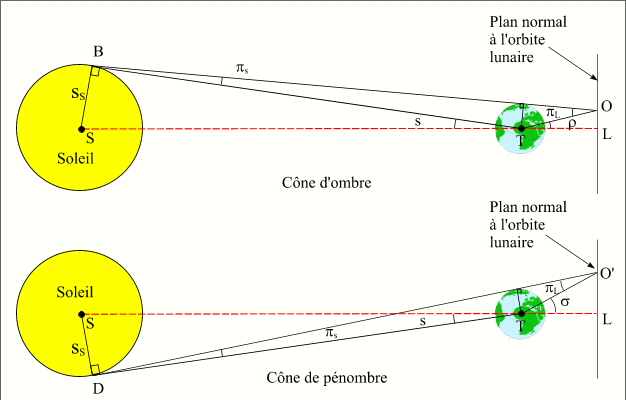
Sur la figure ci-dessus le demi-diamètre apparent géocentrique de la section de l'ombre de la Terre par le plan normal à l'orbite lunaire est égal à l'angle ρ. L'ombre est déterminée par le cône de révolution d'axe ST et de génératrice BO, tangente extérieure au Soleil et à la Terre. Dans le triangle TOB la somme des angles intérieurs π_s et π_L est égale à la somme des angles extérieurs s et ρ. Or par définition π_s est la parallaxe horizontale du Soleil, π_L la parallaxe horizontale de la Lune et s_S est le demi-diamètre apparent du Soleil. Donc ρ est égale à π_s + π_L - s_S.

Ce demi-diamètre ρ est donc maximal lorsque la parallaxe lunaire π_L est maximale et le demi-diamètre apparent π_s est minimal (la parallaxe π_s du Soleil étant pratiquement constante), c'est-à-dire lorsque la Lune est à son périgée et lorsque la Terre est à son aphélie. De même ce demi-diamètre ρ est minimal lorsque la parallaxe lunaire est minimale et le demi-diamètre apparent du Soleil est maximal, c'est-à-dire lorsque la Lune est à son apogée et la Terre à son périhélie.

On peut faire un raisonnement analogue pour le calcul du demi-diamètre apparent géocentrique du cône de pénombre σ. On trouve que σ est égal à π_s + π_L + s_S. Ce demi-diamètre σ est donc maximal lorsque π_L et s_S sont maximales, donc lorsque la Lune est à son périgée et la Terre à son périhélie et il est minimal lorsque π_L et s_S sont minimales, donc lorsque la Lune est à son apogée et la Terre à son aphélie.

On remarquera que la largeur de la couronne de pénombre σ - ρ est bien égale au diamètre apparent du Soleil (2s_S)

Le tableau suivant donne les valeurs extrêmes et moyennes du demi-diamètre s_S apparent du Soleil, de la parallaxe lunaire π_L et du demi-diamètre apparent s_L de la Lune.

	Terre périhélie	Moyenne	Terre aphélie
sS	16'18"	15'59.63"	15'46"
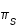
	8.96"	8.80"	8.65"
	Lune périgée	Moyenne	Lune apogée
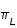
	61' 27"	57' 02,7"	53' 53"
sL	16' 45"	15' 32, 58"	14' 41"

Le tableau suivant donne les valeurs extrêmes et moyennes des demi-diamètres apparents géocentriques du cône d'ombre et du cône de pénombre.

	Minimal	Moyen	Maximal
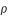
	2263,96" = 37' 43,96" = 2,57 sL	2471,87" = 41' 11,87" = 2,65sL	2749,66" = 45' 49,66" = 2,74 sL
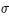
	4187,65" = 1°09' 47,65" = 4,75 sL	4391,13" = 1° 13' 11,13" = 4,71 sL	4673,96" = 1° 17' 53,96" = 4,65 sL

On va voir que ces quantités doivent être augmentées de 1/73 en valeur relative pour ρ et de 1/128 en valeur relative pour σ afin de tenir compte de l'atmosphère terrestre.