| La gravité comme force à distance | Les forces électromagnétiques | Nature de la gravité | Les ondes gravitationnelles : propagation | Ondes gravitationnelles : génération | Les ondes gravitationnelles : détection |
L'espace-temps |
L'équation (6) vous semble complexe ? Les métriques utilisées dans la théorie de la relativité d’Einstein le sont encore plus, parce qu'elles considérent non seulement l'espace, mais aussi l’espace-temps. Dans la théorie de la relativité, c’est le mouvement dans l’espace-temps et non pas le mouvement purement spatial qui nous intéresse.
Pour comprendre ce qu’est l’espace-temps, considérons un corps – par exemple, une boule de billard – qui se déplace sur une surface. Vous pouvez imaginer son mouvement comme une série de photographies instantanées qui montrent sa position (Fig. 1a, cercles bleus pleins) aux temps 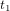 ,
, 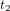 ,
, 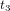 , etc. Imaginez maintenant d’empiler toutes ces photographies instantanées et de tracer une courbe qui connecte les positions du corps dans toutes les photographies instantanées empilées (Fig 1b, courbe bleue continue). Voici la trajectoire du corps dans l’espace-temps. En relativité, on appelle cette trajectoire une ligne d'univers.
, etc. Imaginez maintenant d’empiler toutes ces photographies instantanées et de tracer une courbe qui connecte les positions du corps dans toutes les photographies instantanées empilées (Fig 1b, courbe bleue continue). Voici la trajectoire du corps dans l’espace-temps. En relativité, on appelle cette trajectoire une ligne d'univers.
La Fig. 1b montre une image en trois dimensions (deux dimension spatiales et une dimension temporelle) parce que nous ne nous pouvons pas visualiser une image en quatre dimensions. L'espace-temps réel a quatre dimensions parce l'espace en a trois (les corps ne sont pas contraints à se déplacer sur une surface).
Soit 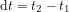 , que nous considérons comme un intervalle de temps infinitésimal, et soient dx, dy, dz les variations entre
, que nous considérons comme un intervalle de temps infinitésimal, et soient dx, dy, dz les variations entre 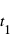 et
et 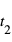 des coordonnées spatiales du corps représenté par le cercle bleu en Fig. 1.
des coordonnées spatiales du corps représenté par le cercle bleu en Fig. 1.
La distance dl parcourue par le corps dans l'intervalle de temps dt est donnée par 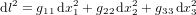 , qui se réduit à
, qui se réduit à 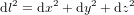 pour la métrique euclidienne en coordonnées cartésiennes. En Fig. 1, les cercles verts montrent la position initiale du corps ; d
pour la métrique euclidienne en coordonnées cartésiennes. En Fig. 1, les cercles verts montrent la position initiale du corps ; d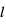 est le déplacement par rapport à la position initiale.
est le déplacement par rapport à la position initiale.
La ligne verte pointillée (Fig. 1b) est la ligne d'univers pour un corps au repos, pour lequel 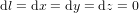 . Pour ce corps, le seul changement est le temps
. Pour ce corps, le seul changement est le temps 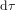 qui s'écoule entre les évènements* A et B. Ce temps-ci est appelé temps propre, parce que c’est le temps dans le référentiel du corps (le référentiel dans lequel le corps est au repos). Le temps propre est indiqué avec la lettre grecque
qui s'écoule entre les évènements* A et B. Ce temps-ci est appelé temps propre, parce que c’est le temps dans le référentiel du corps (le référentiel dans lequel le corps est au repos). Le temps propre est indiqué avec la lettre grecque  pour le distinguer du temps t dans le référentiel de l'observateur . La théorie de la relativité s'appelle comme ça parce que le temps n'est pas absolu. Son écoulement dépend de l'observateur qui le mesure.
pour le distinguer du temps t dans le référentiel de l'observateur . La théorie de la relativité s'appelle comme ça parce que le temps n'est pas absolu. Son écoulement dépend de l'observateur qui le mesure.
Dans le référentiel dans lequel un corps est au repos, 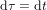 par définition, mais comment mettre en relation le temps propre
par définition, mais comment mettre en relation le temps propre  mesuré par un astronaute qui voyage dans un vaisseau spatial avec le temps t mésuré par un observateur externe, pour lequel l'astronaute se déplace à grande vitesse ? Les transformations de Lorentz répondent à cette question.
mesuré par un astronaute qui voyage dans un vaisseau spatial avec le temps t mésuré par un observateur externe, pour lequel l'astronaute se déplace à grande vitesse ? Les transformations de Lorentz répondent à cette question.
* : *En relativité, un événement est la présence d’un corps dans un point de l’espace à un temps donné (la présence de Telleyrand au Congrès de Vienne en 1815 est un événement).
Considérons un astronef qui part de la planète O et qui voyage à vitesse v constante dans la direction de l'axe x. La planète O se situe à 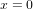 . L'astronaute qui pilote l'astronef et la tour de contrôle sur O ont synchronisé leurs montres à l'instant de départ
. L'astronaute qui pilote l'astronef et la tour de contrôle sur O ont synchronisé leurs montres à l'instant de départ 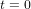 . Pour la tour de contrôle, l'abscisse de l'astronef au temps t est
. Pour la tour de contrôle, l'abscisse de l'astronef au temps t est 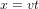 . La ligne droite noire épaisse en Fig. 2 montre la relation entre x et t pour l'astronef dans le référentiel de la tour de contrôle.
. La ligne droite noire épaisse en Fig. 2 montre la relation entre x et t pour l'astronef dans le référentiel de la tour de contrôle.
Au temps 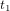 dans son référentiel, la tour de contrôle envoie un message radio à l'astronaute. Le message radio se propage à la vitesse de la lumière (les ondes radio sont des ondes électromagnétiques), donc il va plus vite que l'astronef, même s'il part plus tard. Au temps
dans son référentiel, la tour de contrôle envoie un message radio à l'astronaute. Le message radio se propage à la vitesse de la lumière (les ondes radio sont des ondes électromagnétiques), donc il va plus vite que l'astronef, même s'il part plus tard. Au temps 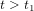 , le message radio a parcouru une distance
, le message radio a parcouru une distance 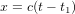 (cette équation correspond à la ligne rouge continue). Quand le message parvient à l'atronaute, l'astronaute répond tout de suite. Les traits rouges montrent la ligne d'univers du message de réponse. La tour de contrôle reçoit la réponse au temps
(cette équation correspond à la ligne rouge continue). Quand le message parvient à l'atronaute, l'astronaute répond tout de suite. Les traits rouges montrent la ligne d'univers du message de réponse. La tour de contrôle reçoit la réponse au temps 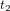 . Nous allons analyser ces événements, d'abord de la perspective de la tour de contrôle, puis de celle de l'astronaute.
. Nous allons analyser ces événements, d'abord de la perspective de la tour de contrôle, puis de celle de l'astronaute.
La Fig. 2 utilise le référentiel de la tour de contrôle. Pour déterminer quand l'astronaute reçoit le message, la tour du contrôle cherche à quel temps t la distance parcourue par le signal radio est égale à celle parcourue par l'astronef. La condition 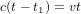 donne
donne 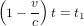 et donc :
et donc :
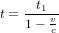 (1).
(1).
Nous avons supposé que l'astronaute répond tout de suite. Donc la distance x entre l'astronef et O est la même quand l'astronaute reçoit le message de la tour et quand il envoie sa réponse. Comme la distance x parcourue par le signal radio est la même dans les deux sens, le temps 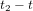 que le message de l'astronaute prend pour parvenir à la tour de contrôle est égal au temps
que le message de l'astronaute prend pour parvenir à la tour de contrôle est égal au temps 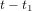 que le message de la tour prend pour parvenir à l'astronaute. La condition
que le message de la tour prend pour parvenir à l'astronaute. La condition 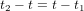 donne :
donne :
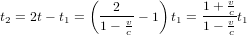 (2).
(2).
Soit  le temps affiché par la montre de l'astronaute quand il reçoit le message de la tour de contrôle. En appliquant le même argument qui amène le personnel de la tour à écrire l'équation (1), l'astronaute conclut que la tour recevra sa réponse au temps :
le temps affiché par la montre de l'astronaute quand il reçoit le message de la tour de contrôle. En appliquant le même argument qui amène le personnel de la tour à écrire l'équation (1), l'astronaute conclut que la tour recevra sa réponse au temps :
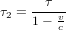 (3)
(3)
La question est quelle est la relation entre les temps  et
et 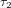 mesurés par l'astronaute et les temps
mesurés par l'astronaute et les temps  et
et 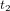 mesurés par la tour. Nous y répondrons en déterminant la valeur du paramètre
mesurés par la tour. Nous y répondrons en déterminant la valeur du paramètre 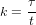 . Notre calcul se base sur un argument de réciprocité. Si le temps
. Notre calcul se base sur un argument de réciprocité. Si le temps  auquel l'astronaute reçoit le message dans son référentiel est k fois le temps t que la tour a calculé dans son référentiel, alors le temps
auquel l'astronaute reçoit le message dans son référentiel est k fois le temps t que la tour a calculé dans son référentiel, alors le temps 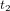 auquel la tour reçoit le message de réponse devra être k fois le temps de réception
auquel la tour reçoit le message de réponse devra être k fois le temps de réception 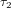 calculé par l'astronaute. Donc :
calculé par l'astronaute. Donc :
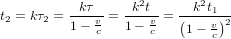 (4),
(4),
où nous avons utilisé (dans l'ordre) l'équation (3), la relation 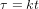 et l'équation (1). Les temps
et l'équation (1). Les temps 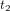 calculés avec l'équation (4) et l'équation (2) doivent être égaux. En posant :
calculés avec l'équation (4) et l'équation (2) doivent être égaux. En posant :
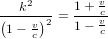 (5)
(5)
on trouve 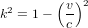 et donc :
et donc :
![\tau^2=\left[1-\left({v\over c}\right)^2\right]t^2](../pages_gravite/equations_gravite-nature/equation96.png) (6).
(6).
Dans le cas limite 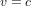 , l'équation (1) donne
, l'équation (1) donne 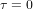 pour n'importe quelle valeur de dt. Pour quelqu'un qui va à la vitesse de la lumière, le temps ne passe pas ! Cela est pourtant impossible pour un corps massif, tel que notre astronef, parce que l'énergie qu'il faudrait pour l'amener à la vitesse de la lumière est infinie. La lumière n'a pas de masse.
pour n'importe quelle valeur de dt. Pour quelqu'un qui va à la vitesse de la lumière, le temps ne passe pas ! Cela est pourtant impossible pour un corps massif, tel que notre astronef, parce que l'énergie qu'il faudrait pour l'amener à la vitesse de la lumière est infinie. La lumière n'a pas de masse.
Notre raisonomment ne contient aucune hypothèse sur la durée du temps t, qui pourrait être très long ou très court. Nous pouvons donc remplacer les temps  et
et  par les temps infinitésimaux
par les temps infinitésimaux 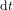 et
et 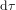 , et réécrire l'équation (6) dans la forme :
, et réécrire l'équation (6) dans la forme :
![{\rm d}\tau^2=\left[1-\left({v\over c}\right)^2\right]{\rm\,d}t^2](../pages_gravite/equations_gravite-nature/equation103.png) (7).
(7).
L'équation (7) est plus générale, parce qu'elle s'applique aussi à des mouvements qui ne sont pas rectilignes uniformes. Même si la vitesse v de l'astronef change avec le temps, elle peut toujours être considérée constante dans des intervalles de temps infinitésimaux. L'équation (7) est connue comme la transformation de Lorentz pour le temps (il y en a une deuxième pour les longueurs).
La vitesse est le déplacement par unité de temps :
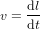 (8).
(8).
En replaçant la vitesse v donnée par l'équation (8) dans l'équation (7), nous trouvons l'expression finale pour le temps propre :
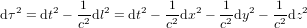 (9),
(9),
qui sera à la base de la discussion qui suit.
L'importance de l'équation (9) est qu'elle nous donne une métrique spatio-temporelle (dite la métrique de Minkowski), par laquelle nous pouvons mesurer la séparation entre deux évenements.
Considérons un point O dans l'espace-temps. Les courbes noires en Fig. 3 nous montrent des trajectoires possibles pour des corps matériaux (massifs). Les lignes rouges correspondent aux trajectoires des rayons lumineux. Ensemble, la totalité des lignes rouges forme une surface biconique, qui définit le cône de lumière de l'événement O. Les lignes jaunes correspondent à des trajectoires interdites. Pour les parcourir, il faudrait se déplacer plus vite que la lumière.
Le passé de l'événement O sont tous les événements dont O aurait pu venir à connaissance et qui auraient pu l'influencer. Pour qu'un événement P puisse influencer O, il faut que de la matière ou de la lumière puisse aller de P à O. P doit donc se situer dans le cône de lumière inférieur, qui correspond au passé de O.
Le futur de O sont tous les événements qui pourront être influencés par O. Pour qu'un événement F puisse être influencé par O, il faut que de la matière ou de la lumière puisse aller de O à F. F doit donc se situer dans le cône de lumière supérieur, qui correspond au futur de O.
Le présent de O sont tous les événements qui n'appartiennent ni à son passé ni à son futur, c'est-à-dire tout ce qui est en dehors son cône de lumière.
L'équation (9) montre que la "distance" spatio-temporelle 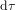 entre O et n'importe quel point sur la surface du cône de lumière est nulle. Avec la définition de distance (c'est-à-dire avec la métrique) en équation (9), la distances entre O et les points A et B en Fig. 3 sont nulles. Cela est logique. Les chemins AO et OB correpondent aux trajectoires d'un rayon de lumière. Pour la lumière, le temps ne passe pas. Donc, pour elle, ces chemins prennent un temps
entre O et n'importe quel point sur la surface du cône de lumière est nulle. Avec la définition de distance (c'est-à-dire avec la métrique) en équation (9), la distances entre O et les points A et B en Fig. 3 sont nulles. Cela est logique. Les chemins AO et OB correpondent aux trajectoires d'un rayon de lumière. Pour la lumière, le temps ne passe pas. Donc, pour elle, ces chemins prennent un temps 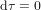 .
.
La distance temporelle, en temps propre, entre P et O ou entre O et F est donnée par 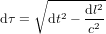 . Le point C appartient au présent de F. La distance temporelle, en temps propre, entre O et C ne correspond à aucun nombre réel parce que, pour les points en dehors du cône de lumière,
. Le point C appartient au présent de F. La distance temporelle, en temps propre, entre O et C ne correspond à aucun nombre réel parce que, pour les points en dehors du cône de lumière, 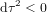 . La distance entre les événements O et C n'est pas temporelle, mais spatiale.
. La distance entre les événements O et C n'est pas temporelle, mais spatiale.
De la même manière que nous avons introduit l'intervalle de temps propre 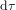 , nous aurions pû introduire la distance propre
, nous aurions pû introduire la distance propre 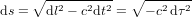 , qui est définie pour tous les événements dans le présent de O, mais devient imaginaire pour les événements passés ou futurs.
, qui est définie pour tous les événements dans le présent de O, mais devient imaginaire pour les événements passés ou futurs.
En conclusion, la métrique relativiste en équation (9) permet de définir une distance en quatre dimensions entre un observateur O et n'importe quel autre événement dans l'espace-temps (un observateur est un événement parce que l'observation est toujours faite à un temps et dans un endroit précis). La distance est temporelle (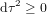 ) pour les événements passés ou futurs. Elle est spatiale (
) pour les événements passés ou futurs. Elle est spatiale (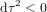 ) pour les événements présents.
) pour les événements présents.
La métrique de Minkowski en équation (9) est la métrique de la théorie de la relativité restreinte. Elle prend en compte la relativité de l'espace et du temps, mais elle est restreinte à un univers plat, qui suit la géométrie euclidienne. Elle ne prend pas en compte les effets de la gravité.
Pour prendre en compte la gravité, il faut passer de la théorie de la relativité restreinte à la théorie de la relativité générale, c'est-à-dire à une métrique plus complexe, de la forme :
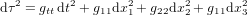 (10),
(10),
où 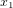 ,
, 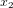 et
et 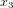 sont les coordonnées spatiales, qui peuvent être les coordonnées cartesiennes orthogonales x, y et z, mais qui pourraient aussi être des coordonnées sphériques, cylindriques, etc.
sont les coordonnées spatiales, qui peuvent être les coordonnées cartesiennes orthogonales x, y et z, mais qui pourraient aussi être des coordonnées sphériques, cylindriques, etc.
On note que, par cohérence dimensionnelle, les coefficients de la métrique ne peuvent pas tous avoir les mêmes unités. Dans la métrique de Minkowski :
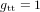 ,
, 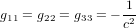 (11)
(11)
Avoir 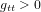 ,
, 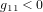 ,
, 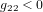 ,
, 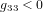 est une propriété générale des métriques dans la théorie de la relativité.
est une propriété générale des métriques dans la théorie de la relativité.
La distribution de la matière-énergie est la source de la gravitation, de la même manière que les charges et les courants sont les sources du champ électromagnétique.
C'est elle qui détermine la métrique (les valeurs des coéfficients 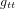 ,
, 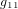 ,
, 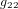 ,
, 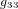 ) et donc la forme du chemin géodésique que les corps vont parcourir sous l'effet de la gravité.
) et donc la forme du chemin géodésique que les corps vont parcourir sous l'effet de la gravité.
Les équations qui permettent de calculer la métrique à partir de la distribution de matière-énergie s'appelent équations d'Einstein.
Leur forme est très compliquée et au-delà du niveau de cette présentation (pour le lecteur avec des connaissances avancées en mécanique classique, les équations d'Einstein généralisent, en quatre dimensions, la forme de l'équation du Poisson pour le champ gravitationnel ; le terme 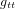 de la métrique est l'équivalent en relativité générale du potentiel gravitationnel en mécanique classique). Notre cours n'a pourtant pas l'objectif de développer des habilités calculatoires. Le but est plutôt de faire comprendre la structure de la théorie de la relativité générale et la conception différente de la gravitation par rapport à la mécanique classique.
de la métrique est l'équivalent en relativité générale du potentiel gravitationnel en mécanique classique). Notre cours n'a pourtant pas l'objectif de développer des habilités calculatoires. Le but est plutôt de faire comprendre la structure de la théorie de la relativité générale et la conception différente de la gravitation par rapport à la mécanique classique.