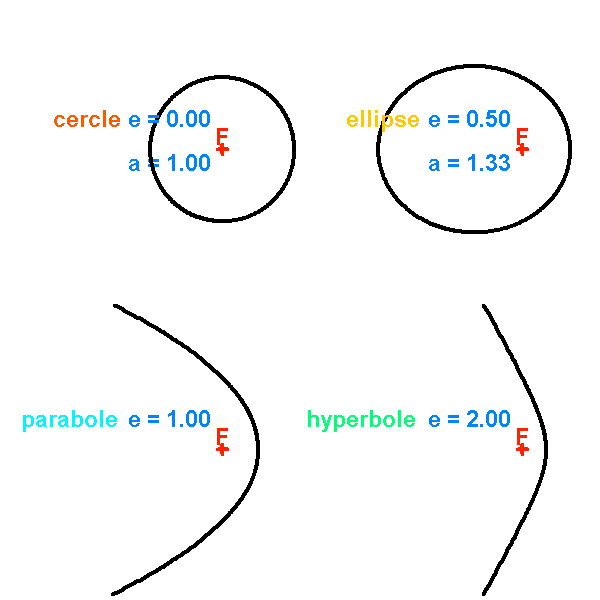
Diverses coniques, selon l'excentricité
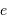
: du cercle
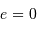
, à l'ellipse
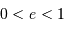
, la parabole
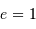
et l'hyperbole
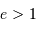
.
Crédit :
ASM
Coniques
Dans le système à 2 corps, les orbites accessibles sont des coniques. Ce terme provient du fait que ces courbes correspondent aux intersections possibles d'un cône de révolution avec un plan.
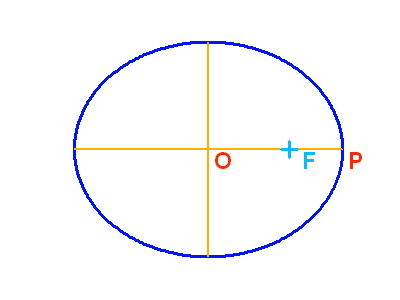
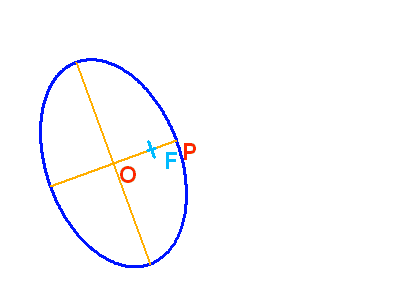
Une ellipse vue dans son plan, et projetée sur le plan du ciel, avec les axes principaux (en orange) et le foyer (croix). La projection du vrai demi-grand axe ne coïncide clairement pas avec le demi-grand axe de l'ellipse projetée. 0 correspond au centre (position conservée par projection), F au foyer occupé par la composante principale (non conservée), et P le périastre.
Crédit :
ASM
Projection d'une orbite elliptique
Les orbites elliptiques observées n'ont aucune raison d'être dans le plan du ciel ; seule leur projection est accessible. Ceci pose problème, car ni l'excentricité ni le demi-grand axe sont conservés par projection. Retrouver ces paramètres nécessitent une reconstruction sérieuse.
Restent néanmoins invariant par projection : le centre, et le rapport OF/OP, qui donne l'excentricité de l'orbite dans son plan
 Objectifs
Objectifs
Présentation des éléments définissant les trajectoires possibles dans le système à 2 corps.
Nature de l'orbite selon l'excentricité ou l'énergie mécanique totale
| excentricité | trajectoire | mouvement | énergie mécanique |
|---|
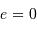 | cercle | lié | minimale et 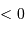 |
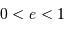 | ellipse | lié | 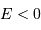 |
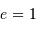 | parabole | libre | 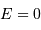 |
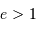 | hyperbole | libre | 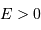 |
Nature de l'orbite selon l'excentricité, dans le cadre du système à 2
corps. La valeur de l'énergie mécanique suppose une référence des énergies potentielles nulle à l'infini.
Trajectoires
Les trajectoires qui sont solution du problème à 2 corps dépendent de l'énergie mécanique totale du système et de son moment cinétique, et peuvent être circulaires, elliptiques, paraboliques ou hyperboliques.
En coordonnées polaires, la trajectoire d'un système dans le cadre du
problème à 2 corps a pour équation paramétrique :
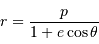
Cette expression peut être obtenue à partir des équations du mouvement
du système à 2 corps par l'étude des équations de Binet (voir un cours de physique), ou par le vecteur excentricité.
Deux paramètres suffisent à définir la trajectoire dans son plan.
- L'excentricité définit la nature
de la conique.
- Le paramètre
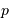 est une longueur reliée au demi-grand axe et à l'excentricité
est une longueur reliée au demi-grand axe et à l'excentricité 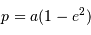 .
.
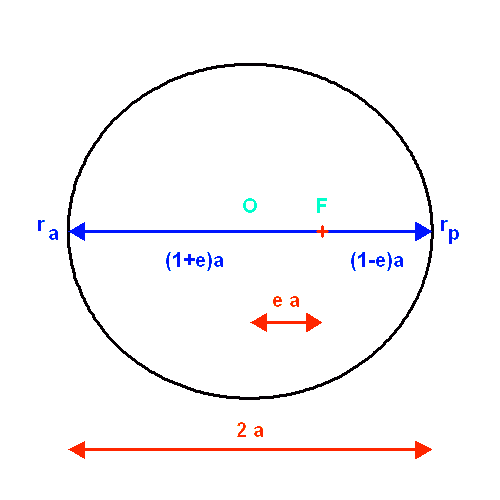
Eléments d'une ellipse : centre
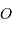
, foyer
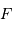
, grand axe
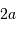
, péri- et apoastre.
Crédit :
ASM
Péri et apoastre : vocabulaire
| astre | périastre | apoastre |
|---|
| Soleil | périhélie | aphélie |
| Terre | périgée | apogée |
Eléments de la trajectoire
- Le rayon vecteur
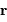 est défini par rapport au foyer
est défini par rapport au foyer 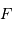 de
l'ellipse définissant le centre de force, et non par rapport au centre
de
l'ellipse définissant le centre de force, et non par rapport au centre 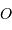 .
. - Le point le plus proche du foyer est le
périastre ; le point le plus
éloigné l'apoastre.
- Le demi-grand axe vérifie
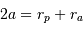 , avec
, avec 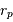 et
et 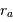 les
rayons des péri- et apoastres
les
rayons des péri- et apoastres 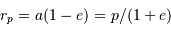
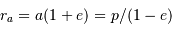
- Le paramètre
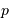 de l'ellipse vérifie
de l'ellipse vérifie 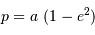
- La distance du centre
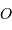 au foyer
au foyer 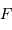 vaut
vaut 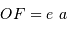
Exemples
- Dans le système solaire, plus un objet est massif, plus sa trajectoire tend à être circulaire ; les astéroïdes ont des trajectoires généralement plus elliptiques que la plupart des planètes.
- Les comètes de longue période ont des trajectoires très elliptiques.
- Les comètes de très longue période ont des trajectoires souvent indéterminées, en fait très sensibles aux perturbations gravitationnelles.
De l'excentricité
Les animations ci-jointes permettent de visualiser l'évolution d'une conique en fonction de son excentricité
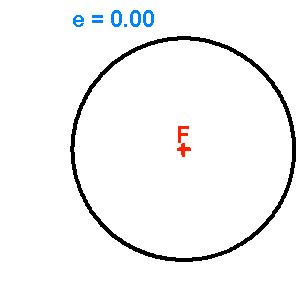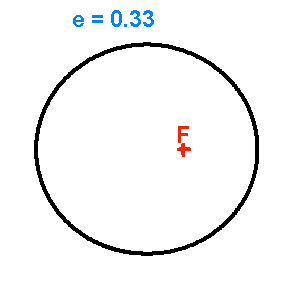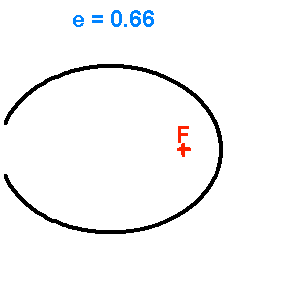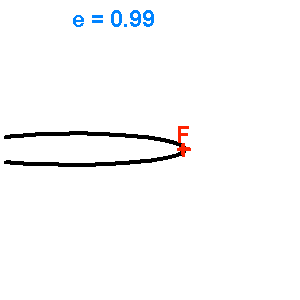
Famille d'ellipses de demi-grand axe fixé, d'excentricité variable
Crédit :
ASM
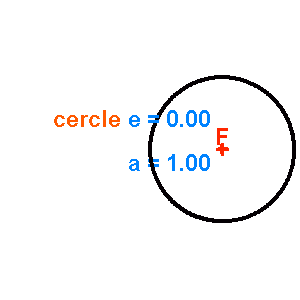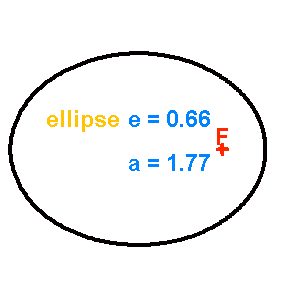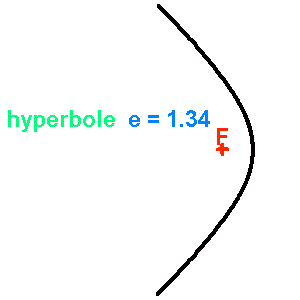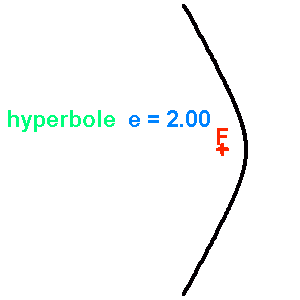
Famille de coniques de paramètre
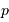
fixé, d'excentricité variable de 0 (cercle) à 2.
Crédit :
ASM
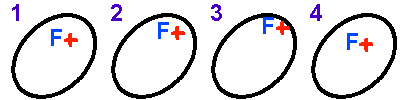
Ellipse reconstruite dans le plan orbital.
Crédit :
ASM
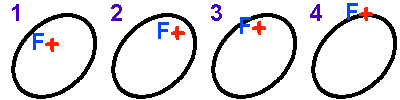
Ellipse observée dans le plan du ciel, distinct du plan orbital
Crédit :
ASM
 QCM
QCM

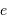 : du cercle
: du cercle 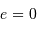 , à l'ellipse
, à l'ellipse 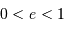 , la parabole
, la parabole 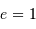 et l'hyperbole
et l'hyperbole 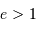 .
.


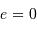
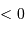
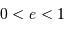
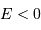
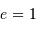
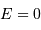
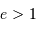
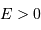
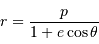
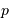 est une longueur reliée au demi-grand axe et à l'excentricité
est une longueur reliée au demi-grand axe et à l'excentricité 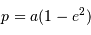 .
.
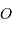 , foyer
, foyer 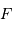 , grand axe
, grand axe 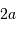 , péri- et apoastre.
, péri- et apoastre.
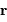 est défini par rapport au foyer
est défini par rapport au foyer 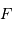 de
l'ellipse définissant le centre de force, et non par rapport au centre
de
l'ellipse définissant le centre de force, et non par rapport au centre 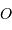 .
.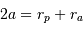 , avec
, avec 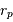 et
et 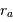 les
rayons des péri- et apoastres
les
rayons des péri- et apoastres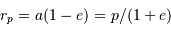
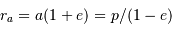
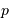 de l'ellipse vérifie
de l'ellipse vérifie 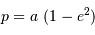
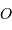 au foyer
au foyer 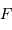 vaut
vaut 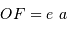


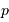 fixé, d'excentricité variable de 0 (cercle) à 2.
fixé, d'excentricité variable de 0 (cercle) à 2.
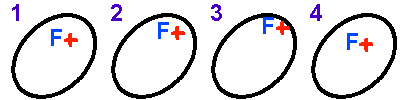
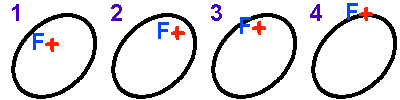
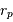 au demi-grand axe
au demi-grand axe 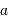 de l'ellipse.
de l'ellipse.
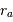 au demi-grand axe
au demi-grand axe 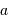 de l'ellipse.
de l'ellipse.
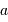 au paramètre
au paramètre 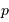 de l'ellipse.
de l'ellipse.