
 Le centre galactique
Le centre galactique
Difficulté : ☆
Temps : 30 min
L'observation du mouvement de
l'étoile S2 autour du centre galactique permet de dégager les propriétés orbitales suivantes.
Il s'agit d'une ellipse de demi-grand axe 0.119", parcourue en une période de 15.2 ans, avec une excentricité de 0.87.
Question 1)
Pourquoi l'approximation du système à 2 corps semble-t-elle convenable ?
AideSolution
Quelle est la nature de l'orbite ?
L'orbite, elliptique, annonce un mouvement képlérien.
Question 2)
Le Soleil se situant à 8000 pc du centre galactique,
estimer le demi-grand axe de l'orbite en UA
AideAideSolution
Application directe de la définition de la parallaxe
1" à 1 pc correspond à 1 UA
Comme 1" à 1 pc correspond à 1 UA, 0.119" à 8000 pc correspondent à
environ 950 UA.
Question 3)
En déduire la masse 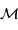 du centre galactique, en masse solaire.
du centre galactique, en masse solaire.
AideAideSolution
Application directe du cours sur la 3e loi de Kepler.
Écrire la 3e loi de Kepler dans le système d'unités : année, unité astronomique, masse du Soleil
La 3e loi de Kepler s'écrit, dans le système d'unités proposé :
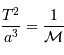
L'application numérique donne : 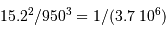 . L'étoile S2 orbite donc dans un potentiel central créé par une masse de l'ordre de 3.7 millions de fois la masse du Soleil.
. L'étoile S2 orbite donc dans un potentiel central créé par une masse de l'ordre de 3.7 millions de fois la masse du Soleil.
Question 4)
Estimer la valeur du péricentre 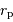 , en UA
, en UA
AideAideSolution
Application du cours : 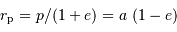
Application du cours, le lien entre périastre, demi-grand axe et excentricité s'écrit :
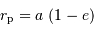
L'application numérique donne 123 UA.
Question 5)
L'orbite de S2 apparaissant rigoureusement elliptique, comme le prévoit la mécanique képlerienne, on peut supposer que la taille caractéristique du corps central permet l'application de la mécanique du point. En d'autres termes, ce centre de force s'inscrit dans un rayon bien moindre que le péricentre... et serait un trou noir.
Estimer alors l'horizon de ce trou noir de masse 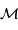 .
.
AideSolution
Application du cours : 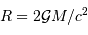
La vitesse de libération du trou noir vaut 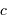 , par définition, donc :
, par définition, donc :
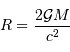
La conversion de la masse 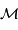 en masse solaire
en masse solaire 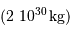 donne, pour l'application numérique
donne, pour l'application numérique 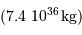 :
:
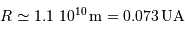
Question 6)
Estimer la vitesse de S2 au péricentre (le rayon de courbure 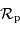 de la trajectoire au péricentre est égal au paramètre
de la trajectoire au péricentre est égal au paramètre 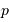 de l'ellipse, soit
de l'ellipse, soit 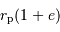 ).
).
AideAideAideSolution
Au voisinage du péricentre, l'accélération de S2 n'est que normale.
L'accélération normale vaut 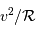 , avec
, avec 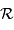 le rayon de courbure.
le rayon de courbure.
Appliquer la relation newtonienne liant force et accélération normale.
Au voisinage du péricentre 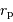 , l'accélération de S2 n'est que normale.
L'accélération normale est égale au champ gravitationnel, càd :
, l'accélération de S2 n'est que normale.
L'accélération normale est égale au champ gravitationnel, càd :
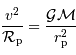
D'où l'expression de la vitesse :
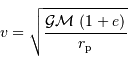
L'application numérique donne alors, avec 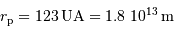 :
:
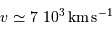 , soit 2.3 % de la vitesse de la lumière.
, soit 2.3 % de la vitesse de la lumière.

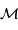 .
.