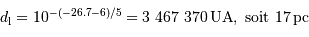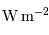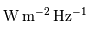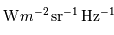Mesurer une grandeur énergétique n'est pas des plus simples. En fonction des besoins de l'astronomie et de l'astrophysique s'est développée la notion de magnitude.
Les pages qui suivent définissent cette échelle énergétique, et justifient son emploi en fonction des mesures effectuées.
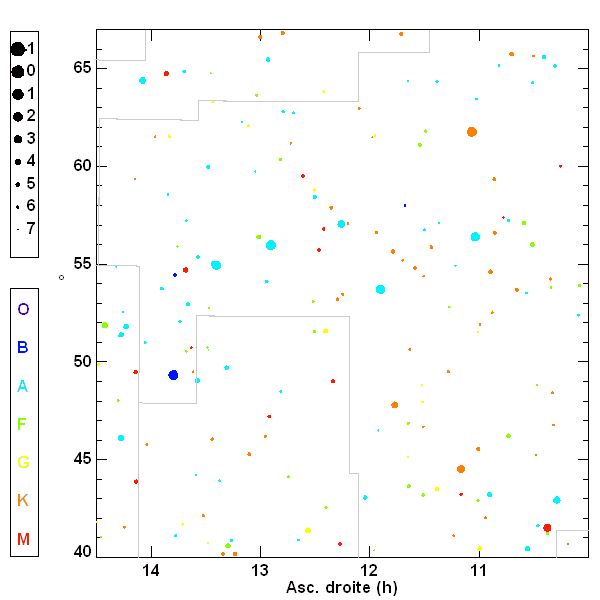
La constellation de la Grande Ourse. La taille des points code la magnitude stellaire, la couleur le type spectral.
Crédit :
BSC/ASM
Grandeur des étoiles
Il n'y a pas de lien univoque entre la luminosité d'une étoile et sa taille. Dans le langage commun, une "grosse" étoile est une étoile lumineuse, et une "petite" une étoile moins lumineuse.
Historiquement est apparue la notion de grandeur, ici rendue par la représentation d'un champ stellaire.
Figure historique

Croquis d'un champ stellaire dans la Nébuleuse d'Orion (1771). Le cartouche définit le codage de la grandeur, ou luminosité,
des étoiles
Crédit :
Bibliothèque de l'Observatoire de Paris
Magnitude
Pour coder les magnitudes, souvent les cartes reprennent cette image
(voir le cours corps noir pour la relation entre rayon et flux stellaires).
Magnitudes
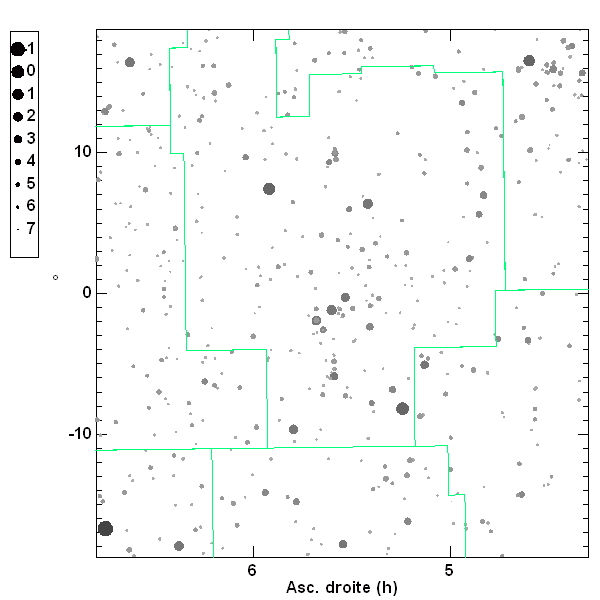
La constellation d'Orion, avec représentation des magnitudes stellaires.
Par convention, la magnitude d'une étoile est souvent représentée par un disque d'autant plus gros que la magnitude est faible (càd que l'objet est lumineux).
Crédit :
ASM
 Objectifs
Objectifs
La magnitude exprime une mesure photométrique dans un système d'unités approprié à l'usage astrophysique. On peut ainsi comparer les étoiles les unes par rapport aux autres d'un point de vue énergétique.
Historique
Le père de la magnitude est Hipparque (2e siècle avant J-C) : les étoiles les plus brillantes étaient classées dans la catégorie "étoiles de première grandeur", les autres se répartissaient ensuite sur 5 échelons, jusqu'aux "étoiles de sixième grandeur" qui étaient les plus faibles visibles à l'œil nu.
L'utilisation d'instruments capables de mesurer les intensités lumineuses plus précisément qu'à l'oeil nu permit de préciser et de développer la notion de magnitude : la définition historique de la magnitude a été traduite en une échelle logarithmique, car l'oeil est un
récepteur logarithmique. La limite de détection à l'oeil nu, correspond à des étoiles de magnitude 6.
Magnitude apparente
Etoile double du Bouvier

L'étoile centrale a une magnitude de 4,5, la seconde étoile a une magnitude de 7,2 et les étoiles du fond de ciel une magnitude comprise entre 15 et 18.
Crédit :
CDS
La magnitude apparente mesure l'"éclat" apparent d'une étoile, c'est à dire la façon dont on la voit de la Terre.
Quelques magnitudes apparentes
| Objet | Magnitude apparente |
|---|
| Soleil | -26,7 |
| Lune | -12,7 |
| Vénus | -4,4 |
| Sirus | -1,4 |
| Véga | 0 |
| Antarès | 1 |
| Etoile polaire | 2 |
| Limite de perception à l'oeil nu | 6 |
| Limite de perception aux jumelles | 10 |
| Limite de perception au sol | 27 |
| Limite de perception du télescope spatial Hubble | 30 |
Plus un objet est brillant, plus sa magnitude est petite. Une
différence de magnitude de 2.5 unités correspond à un contraste de
luminosité de 10.
Magnitude apparente
 Définition
Définition
La magnitude est une grandeur qui permet de mesurer la luminosité des astres.
La magnitude apparente 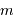 d'une étoile est définie conventionnellement à partir de son flux
d'une étoile est définie conventionnellement à partir de son flux 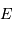 par la relation :
par la relation :
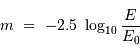
où 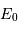 représente le flux
d'une étoile de référence de magnitude nulle.
représente le flux
d'une étoile de référence de magnitude nulle.
Le facteur 2.5 et la base logarithmique décimale ont été choisis afin de respecter la définition historique.
La définition du flux ici introduit n'est pas primordiale, vu que la définition se contente d'introduire un rapport de cette grandeur. On peut se référer à un tableau récapitulatif des grandeurs photométriques utilisées.
La différence de magnitude de deux étoiles, 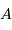 et
et 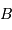 , s'exprime par :
, s'exprime par :
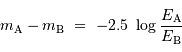
Elle est égale à 2.5 en valeur absolue si le rapport de leurs flux est 10.
D'autres échelles de magnitude
La magnitude apparente ne nous renseigne en rien sur la luminosité réelle de l'astre et ne donne aucune indication sur sa nature, car la définition de la magnitude apparente :
- ne dépend pas a priori du récepteur utilisé,
- ne dépend que de l'éclat apparent de l'objet et donc mélange une information propre à l'étoile (son flux) à la distance Terre-étoile,
- ne tient pas compte de la couleur de l'étoile,
- ne nécessite pas une définition précise de la grandeur photométrique mesurée, vu que seul le rapport de deux telles grandeurs entre en jeu.
Des définitions plus circonstanciées permettent de préciser la notion de magnitude.
On introduit la magnitude absolue 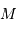 , qui indique la luminosité d'un objet rapporté à une distance de 10 parsec.
, qui indique la luminosité d'un objet rapporté à une distance de 10 parsec.
De même, la définition précédente néglige toute information sur la couleur de l'objet. Pour cela, on introduit la magnitude monochromatique et les indices de couleur.
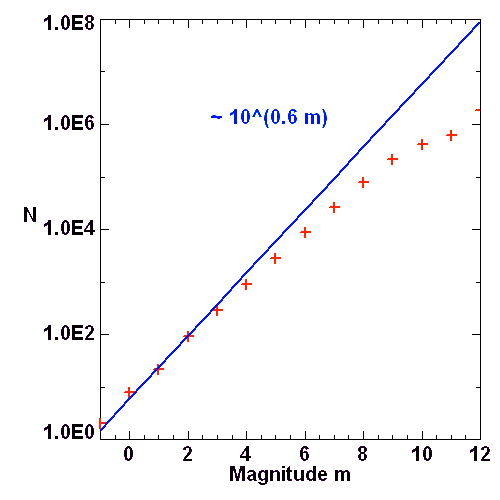
Décompte des cibles stellaires jusqu'à la magnitude 12. La loi en
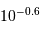
n'est plus vérifiée à grande distance, l'absorption interstellaire et la taille finie de l'épaisseur du bras galactique conduisant à un déficit de magnitudes faibles.
Crédit :
ASM
 Luminosité et éclairement
Luminosité et éclairement
Difficulté : ☆
Temps : 10 min
La luminosité correspond à la puissance totale rayonnée par l'étoile.
Lorsque cette puissance est considérée par unité de surface, on parle
de puissance surfacique. On définit l'éclairement 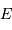 d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
Question 2)
Calculer la puissance surfacique reçue
sur Terre d'une étoile de type solaire située à la distance de Proxima
de Centaure, de parallaxe annuelle 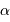 = 0.76". On donne
= 0.76". On donne 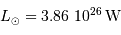 .
.
Question 3)
De même, calculer la puissance surfacique
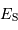 du Soleil reçu sur Terre.
du Soleil reçu sur Terre.
 Magnitude apparente
Magnitude apparente
Difficulté : ☆
Temps : 15 min
Question 1)
Rappeler la définition de la magnitude apparente d'une étoile.
Question 2)
Deux étoiles ont des éclairements apparents 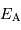 et
et 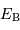 . Exprimer leur différence de magnitude.
. Exprimer leur différence de magnitude.
Question 3)
Comparer les flux d'objets de magnitudes -26.7 (soleil), -2.55 (Jupiter), +6 (étoiles juste visibles à l'oeil nu), +27 (magnitude limite accessible au sol).
 Performance de détection liée à la taille du récepteur
Performance de détection liée à la taille du récepteur
Difficulté : ☆
Temps : 25 min
En vision nocturne, le diamètre de notre pupille vaut de l'ordre de 6 mm, et la magnitude limite visible à l'oeil nu est 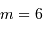 .
.
On rappelle l'expression de 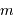 , la magnitude apparente d'un objet :
, la magnitude apparente d'un objet :
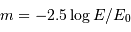
avec 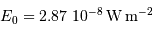 pour le domaine visible.
pour le domaine visible.
Question 1)
Exprimer 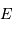 , le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de
, le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de 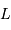 et
et 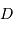 , respectivement la puissance totale reçue et le diamètre de la pupille.
, respectivement la puissance totale reçue et le diamètre de la pupille.
Par définition, l'éclairement découle de la luminosité :
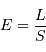
Question 2)
Calculer 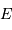 et
et 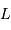 pour une étoile de magnitude 6.
pour une étoile de magnitude 6.
Question 3)
Montrer qu'avec un collecteur de diamètre 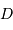 , l'oeil a accès aux magnitudes jusqu'à :
, l'oeil a accès aux magnitudes jusqu'à :
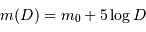
avec 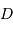 exprimé en m. Identifier
exprimé en m. Identifier 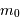
Question 4)
Calculer 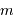 , pour
, pour 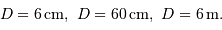
Question 5)
Comment procède-t-on pour observer les objets de magnitude supérieure?
 Compter les étoiles
Compter les étoiles
Difficulté : ☆
Temps : 20 min
Le but de cet exercice est de compter les étoiles en fonction de leur
magnitude. Pour se faire, on pose deux hypothèses :
- toutes les étoiles présentent la même magnitude absolue,
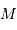 .
. - la répartition des étoiles autour du soleil est uniforme,
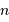 .
.
Question 1)
Déterminer la magnitude apparente d'une étoile à la distance 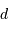 .
.
Revoir le cours, et la définition
de la magnitude absolue.
Question 2)
Dénombrer le nombre d'étoiles 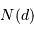 dans une sphère de rayon
dans une sphère de rayon 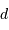 autour du
soleil.
autour du
soleil.
Le volume d'une sphère de rayon 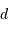 est... allons, un petit effort
est... allons, un petit effort
...
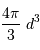
Question 3)
A partir des deux relations précédemment établies, montrer que le nombre
d'étoiles jusqu'à la magnitude 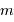 évolue comme :
évolue comme :
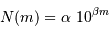
Identifier le coefficient 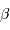 de l'exposant
de l'exposant
Eliminer la variable 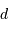 des équations précédentes
des équations précédentes
D'après ce qui précède, le rayon 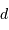 , exprimé en parsec, s'exprime en fonction des magnitudes par
, exprimé en parsec, s'exprime en fonction des magnitudes par
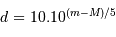
Question 4)
Estimer 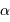 , sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
, sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
Question 5)
Ce résultat apparaît-il en accord avec le nombre d'étoiles plus brillantes que la magnitude 0
 Différence de magnitude
Différence de magnitude
Difficulté : ☆
Temps : 20 min
Question 1)
Deux étoiles d'un système double présentent une différence de magnitude
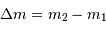 .
Exprimer le rapport de leurs luminosités
.
Exprimer le rapport de leurs luminosités 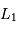 et
et 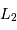
[2 points]
Question 2)
Faire l'application numérique pour 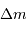 = 1,
= 1, 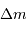 = 10
= 10
[1 points]
 Le projet OWL
Le projet OWL
Difficulté : ☆
Temps : 20 min
Le projet OWL (overwhelmingly large telescope) de l'ESO s'est attaché à étudier le concept d'un télescope avec un collecteur de diamètre 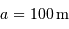 . Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
. Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
Question 1)
Estimer le gain attendu en magnitude limite observable avec un télescope de 100 m, par rapport à un télescope de 10 m.
[1 points]
Question 2)
Ce télescope étant muni d'une optique adaptative, il donnera accès à une résolution angulaire proche de la limite de diffraction 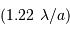 . Calculer cette limite pour le visible.
. Calculer cette limite pour le visible.
[1 points]
Couleur
Les étoiles présentent des couleurs différentes, ce qu'il va falloir retranscrire sur leur magnitude.
Constellation d'Orion

La constellation d'Orion, avec reproduction des couleurs par superposition de 3 clichés enregistrés dans des bandes spectrales différentes.
Crédit :
CFHT
Magnitude monochromatique et indice de couleur
Les étoiles rayonnent pratiquement comme des corps noirs. Elles ont un maximum d'intensité lumineuse qui varie avec la température de leur couche externe. L'échelle de magnitude UBVRI (UV, Bleu, Visible, Rouge, Infrarouge), correspond aux magnitudes d'une étoile dans une gamme de longueur d'onde de l'UV à l'IR.
Filtres BVRI

La mesure précise des magnitudes monochromatiques nécessite l'emploi de filtres dans un système bien prédéfini.
Crédit :
ESO/Cyril Cavadore
Imager dans différents domaines spectraux permet de distinguer des objets avec une couleur particulière.

Quatre images du ciel profond dans 4 couleurs différentes, du proche UV au rouge. Un des objets du champ - en fait une galaxie très lointaine - n'est visible que dans le rouge : sa magnitude dans l'UV et le bleu est trop grande.
Crédit :
HST
Indice de couleur
Les variations de luminosité d'un objet permettent de remonter à la couleur de cet objet... à moins que le milieu interstellaire ne soit pas transparent.

La nébuleuse d'Orion, vue en visible en proche infrarouge. Les différences d'aspect sont ici essentiellement dues à des effets d'absorption par la matière interstellaire.
Crédit :
HST
Analyse multispectrale
Le centre galactique dans diverses couleurs 
L'analyse multispectrale est indispensable pour caractériser complètement un objet : ce qui apparaît en émission dans un domaine spectral peut être absorbant dans un autre.
Température et indice de couleur
L'indice de couleur, corrigé de toute absorption, permet de remonter à la température de l'objet.
Magnitude et indice de couleur 
A l'aide du tableau, identifier les températures d'un lot d'étoiles.
 Magnitude et temps de pose
Magnitude et temps de pose
Difficulté : ☆
Temps : 45 min
Détecter une source lumineuse, quelqu'elle soit, nécessite la collecte d'un nombre suffisant de photons, ce qui requiert un temps de pose adapté à la magnitude. On se place dans des conditions d'observation en bande V (largeur spectrale 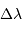 ), avec une chaîne de rendement total
), avec une chaîne de rendement total 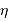 . Ce rendement tient compte de la collecte des photons jusqu'à leur transformation en photo-électrons. On note
. Ce rendement tient compte de la collecte des photons jusqu'à leur transformation en photo-électrons. On note 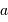 le diamètre collecteur.
le diamètre collecteur.
Question 1)
Rappeler l'expression qui relie l'éclairement monochromatique 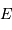 à la magnitude
à la magnitude 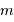 de la source.
Quelles grandeurs de la chaîne de collecte interviennent pour traduire cet éclairement monochromatique en puissance ?
de la source.
Quelles grandeurs de la chaîne de collecte interviennent pour traduire cet éclairement monochromatique en puissance ?
[1 points]
Question 2)
Montrer que le nombre de photons à collecter s'exprime, en fonction des données et du temps de pose 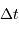 .
.
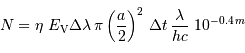
[2 points]
L'unité de l'éclairement monochromatique permet d'imaginer le résultat.
L'énergie d'un photon vaut 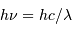 .
.
Question 3)
Faire l'application numérique avec les données concernant la bande V, pour une source de magnitude 10, un télescope de la classe 8 m, une pose de 1 s, un rendement de 10%.
[1 points]
Se prendre par la main et se lancer dans l'application numérique.
Question 4)
Que devient le temps de pose pour une source de magnitude 20 ? Quel temps de pose faut-il viser pour collecter 1000 photons sur une source de magnitude 25 ? Et pour collecter 100 photons/pixel sur une source (supposée uniforme) de magnitude 25 étendue sur 100 pixels ?
[2 points]
De l'intérêt d'un paramètre absolu
La magnitude apparente, comme son nom l'indique, n'est qu'apparente pour un observateur donnée. Elle dépend de la source et de son identité, mais aussi de l'observateur : ce point est gênant si l'on s'intéresse à l'objet pour ses seules propriétés. Pour faire de la physique et ainsi s'affranchir de l'effet de distance, on utilise la notion de magnitude absolue.
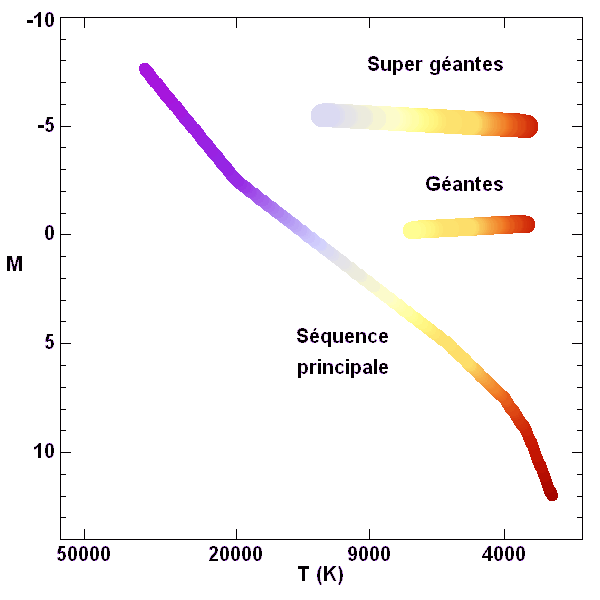
Ce
diagramme HR mesure, sur l'axe des ordonnées, la luminosité stellaire en magnitude absolue.
Crédit :
ASM
Module de distance
La quantité 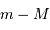 porte le nom de module de distance. En reliant la distance à une différence de magnitude, ce module indique la distance en échelle logarithmique.
porte le nom de module de distance. En reliant la distance à une différence de magnitude, ce module indique la distance en échelle logarithmique.
Module de distance
| Objet | module de distance | distance au Soleil (pc) |
| référence | 0 | 10 |
| L'amas des Hyades | 3.3 | 48 |
| Les Nuages de Magellan | 18.5 | 50 000 |
| La galaxie d'Andromède | 24.1 | 890 000 |
Le module de distance est nul, par définition, pour une distance de 10 pc ; il vaut 5 pour une distance de 100 pc, 10 pour une distance de 1000 pc.
Correction de l'absorption
Pour passer de la magnitude apparente à la magnitude absolue,
on est amené à corriger, en plus de la distance, les effets
dus à une éventuelle absorption interstellaire. Cette absorption est provoquée par divers éléments (poussières, gaz) présent sur la ligne de visée. Alors, la magnitude
absolue s'exprime en fonction de la magnitude apparente par :
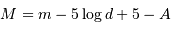
Le terme d'absorption 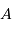 ne peut être que positif ; ne pas en tenir compte conduit à surestimer la magnitude absolue, càd à sous-estimer la luminosité de l'objet.
ne peut être que positif ; ne pas en tenir compte conduit à surestimer la magnitude absolue, càd à sous-estimer la luminosité de l'objet.
Magnitude bolométrique
A l'opposé de la magnitude monochromatique, la magnitude bolométrique mesure l'énergie rayonnée sur l'ensemble du spectre électromagnétique. Mesurer une telle magnitude n'est pas chose aisée, et s'obtient le plus souvent par extrapolation à partir de la magnitude absolue mesurée dans quelques bandes spectrales.
Détermination de la magnitude absolue
Etoiles proches et brillantes 
On cherche à estimer les magnitudes absolues des étoiles les plus brillantes du ciel, leur distance étant mesurée par ailleurs.
- Rappeler le lien entre les magnitudes apparente, absolue et la distance
- Calculer à l'aide du TabloGraphe (mode d'emploi si nécessaire) la magnitude absolue
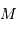 .
. - Tracer le diagramme HR de ce lot d'étoiles : appartiennent-elles majoritairement à la séquence principale ?
 Magnitude absolue ; magnitude/distance
Magnitude absolue ; magnitude/distance
Difficulté : ☆
Temps : 20 min
Question 2)
La magnitude apparente visible du soleil est de -26.7. Que vaut sa magnitude absolue?
Rappel : 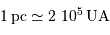
Question 3)
Que vaudrait la magnitude apparente du Soleil à la distance de Proxima du Centaure (1.33 pc)? A la distance du centre galactique (8 kpc)?
Question 4)
L'oeil humain peut distinguer les magnitudes inférieures à 6. Jusqu'à quelle distance une étoile de type solaire reste-t-elle visible à l'oeil nu?
 Magnitude absolue et absorption
Magnitude absolue et absorption
Difficulté : ☆☆
Temps : 15 min
Question 1)
Rappeler la relation définissant la magnitude absolue, tenant compte de
l'absorption 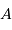 .
.
[1 points]
Question 2)
Ne pas tenir compte de l'absorption revient-il à surestimer ou
sous-estimer la magnitude absolue d'un objet?
[1 points]
Question 3)
Ne pas tenir compte de l'absorption revient-il à surestimer ou
sous-estimer la distance d'un objet?
[1 points]
Question 4)
Sans tenir compte de l'absorption, on déduit pour une Céphéïde, d'après
la relation magnitude absolue-période, une distance au soleil 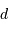 =
20 kpc. Comment est corrigée cette distance si l'on tient compte d'un
coefficient d'absorption de 0.2 magnitude ? Conclure.
=
20 kpc. Comment est corrigée cette distance si l'on tient compte d'un
coefficient d'absorption de 0.2 magnitude ? Conclure.
[1 points]
Bilan
La magnitude apparente, qui mesure l'éclat apparent de l'étoile, est le
paramètre observable ; mais elle ne renseigne pas sur le paramètre
intrinsèque de celle-ci, qui est sa
luminosité.
Cette grandeur est retranscrite par la magnitude absolue.
Une étoile de magnitude absolue donnée apparaît à une magnitude apparente d'autant plus grande (= moins lumineuse) qu'elle est plus éloignée.
Enfin, s'il est possible
d'attribuer une magnitude absolue à une étoile, à partir de critères
d'observation, on peut déterminer sa distance en mesurant sa magnitude
apparente et en la comparant à la magnitude absolue.
 Remarque
Remarque
La luminosité et l'éclat apparente des objets tels que les planètes, les satellites et autres petits corps peuvent aussi être exprimées via la notion de magnitude. Comme la luminosité visible provient en grande partie de la réflexion
du flux solaire, la magnitude de tels objets est très complexe, car elle
dépend des distances objet-Soleil et objet-Terre, de la surface du
corps, de la présence ou non d'une atmosphère, etc...
Avertissement !
Plusieurs échelles énergétiques cohabitent en astrophysique,
certaine classiques (eV et multiples...), d'autres spécifiques
(Jansky, magnitude, K ...). Si d'une part les termes en usage en astronomie ne correspondent pas nécessairement aux définitions radiométriques, rien ne garantit dans un document donné l'adéquation exacte entre le sens local et la définition plus générale !
Pour s'y retrouver, il faut le plus souvent veiller à la cohérence d'un terme par rapport à sa définition donnée, et s'appuyer sur son unité.
Définitions
Définitions, à propos du rayonnement
d'une étoile :
- La luminosité
correspond à la puissance totale rayonnée. Comme toute puissance, elle
se mesure en watts (SI).
- Lorsque cette puissance est
considérée par unité de surface, on parle d'éclairement, ou de flux.
- Si la
dépendance en fonction de la couleur apparaît, on définit la
densité spectrale d'éclairement ou éclairement monochromatique,
mais il faut préciser si l'intervalle spectral est divisé
selon la longueur d'onde du photon, ou bien selon sa fréquence... ou selon toute autre unité spectrale.
- La notion de luminance ou d'intensité rend compte de l'émission par unité d'angle
solide. C'est elle qui intervient dans la loi de rayonnement du corps noir.
Définitions de grandeurs photométriques
| Grandeur | (terme en radiométrie) | Définition | Unité  |
|---|
| Puissance, luminosité | (flux) | Puissance | W |
| Radiance | (émittance) | Puissance émise par unité de surface normale à la propagation | 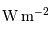 |
| Eclairement, flux | (irradiance) | Puissance reçue par unité de surface normale à la propagation | 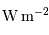 |
| Luminance, brillance | (radiance) | Puissance par unité de surface normale à la propagation, et par unité d'angle solide | 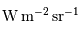 |
| Eclairement monochromatique | | Puissance par unité de surface et par unité spectrale | 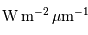 |
| Intensité, luminance monochromatique | | Puissance transportée par unité spectrale, par unité d'angle solide, et par unité d'élément de surface | 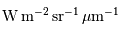 |
 avec comme unité spectrale la longueur d'onde exprimée en micromètre.
avec comme unité spectrale la longueur d'onde exprimée en micromètre.
 Conversions
Conversions
Difficulté : ☆
Temps : 20 min
Question 1)
Reprendre les unités du tableau définissant les grandeurs photométriques, et les redéfinir dans le cas où l'unité spectrale choisie pour le rayonnement est la fréquence, en Hertz, et non le micromètre.
Identifier pour chaque unité la dépendance spectrale en 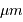 .
.
Magnitude apparente, monochromatique... toutes ces définitions prennent leur importance pour rendre compte des observations et donner accès à des mesure telle la magnitude absolue, corrigée de la distance d'observation, et propriété intrinsèque de l'objet.

Quasar de magnitude 24.5 (amplifié gravitationnellement), avec un décalage spectral z = 4.0, observé à un âge correspondant aux premiers 10% de l'âge de l'Univers.
Crédit :
ESO
- Question 1
Aide :
Revoir le cours, et la définition
de la magnitude absolue.
Solution :
Par définition de la magnitude absolue :
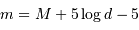
- Question 2
Aide :
Le volume d'une sphère de rayon 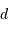 est... allons, un petit effort
est... allons, un petit effort
Aide :
...
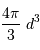
Solution :
Le volume de la sphère de rayon 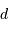 multiplié par la densité stellaire donne le nombre d'étoiles :
multiplié par la densité stellaire donne le nombre d'étoiles :
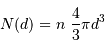
- Question 3
Aide :
Eliminer la variable 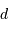 des équations précédentes
des équations précédentes
Aide :
D'après ce qui précède, le rayon 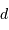 , exprimé en parsec, s'exprime en fonction des magnitudes par
, exprimé en parsec, s'exprime en fonction des magnitudes par
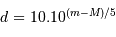
Solution :
De 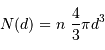 et
et
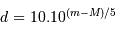 , il sort immédiatement :
, il sort immédiatement :
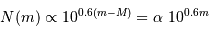
- Question 4
Solution :
Il s'agit pour 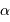 de vérifier :
de vérifier :
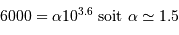
- Question 5
Solution :
Le facteur 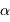 s'identifie à
s'identifie à 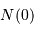 , nombre d'étoiles de magnitude
inférieure à
, nombre d'étoiles de magnitude
inférieure à 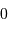 . Si l'on se réfère au
tableau, recensant les objets les plus
brillants, l'ordre de grandeur est correct.
. Si l'on se réfère au
tableau, recensant les objets les plus
brillants, l'ordre de grandeur est correct.
- Question 1
Aide :
L'oeil est sensible à la lumière... visible, du bleu au rouge. La réponse est maximale dans les couleurs verte et jaune, faible dans le rouge et le bleu.
Les données du tableau Apprendre doivent être adaptées.
Pour tenir compte du fait que l'oeil a un domaine de réception plus large que l'intervalle spectral dans la bande photométrique standard V, on prendra un intervalle équivalent de largeur 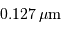 .
.
Solution :
Dans le domaine visible, par définition, la relation entre magnitude et éclairement monochromatique s'écrit :
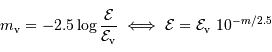
On a la même relation avec l'éclairement (intégré sur la bande spectrale) :
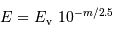
La valeur de l'éclairement 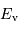 de référence se calcule par:
de référence se calcule par:
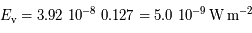
La réponse de l'oeil humain couvre un intervalle de presque 400 nm, mais avec une très faible réponse dans le bleu et le rouge ; ceci justifie la valeur de 127 nm introduite ici.
Le calcul de l'éclairement 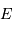 devient alors simplement :
devient alors simplement :
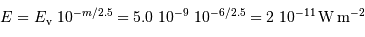
Il en découle la puissance 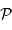 :
:
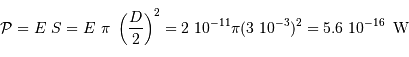
- Question 2
Aide :
Energie 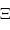 d'un photon de longueur d'onde
d'un photon de longueur d'onde 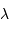 :
:
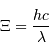
où 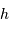 est la constante de Planck
est la constante de Planck 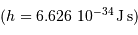 , et
, et 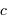 la célérité de la lumière dans le vide.
la célérité de la lumière dans le vide.
Solution :
L'énergie reçue pendant 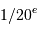 de seconde vaut :
de seconde vaut :
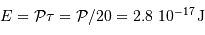
L'énergie d'un photon de longueur d'onde 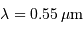 étant:
étant:
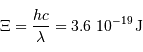
On en déduit le nombre de photons 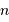 correspond à cette énergie intégrée pendant
correspond à cette énergie intégrée pendant 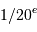 de seconde sur la rétine :
de seconde sur la rétine :
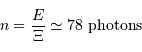




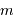 d'une étoile est définie conventionnellement à partir de son flux
d'une étoile est définie conventionnellement à partir de son flux 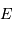 par la relation :
par la relation :
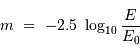
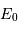 représente le flux
d'une étoile de référence de magnitude nulle.
représente le flux
d'une étoile de référence de magnitude nulle.
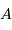 et
et 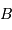 , s'exprime par :
, s'exprime par :
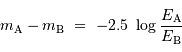
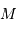 , qui indique la luminosité d'un objet rapporté à une distance de 10
, qui indique la luminosité d'un objet rapporté à une distance de 10 
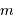 , décompte du nombre
, décompte du nombre 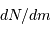 d'étoiles de magnitude comprise dans l'intervalle
d'étoiles de magnitude comprise dans l'intervalle ![[m-0.5, m+0.5]](../pages_luminosite/equations_magnitude-apparente/equation11.png) , et total cumulé
, et total cumulé 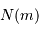 jusqu'à la magnitude
jusqu'à la magnitude 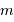 .
.
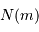 , et à montrer qu'elle est
du type :
, et à montrer qu'elle est
du type :
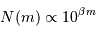
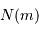 observables jusqu'à une
magnitude apparente donnée
observables jusqu'à une
magnitude apparente donnée 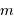 , puis
, puis 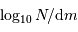 en fonction de
en fonction de 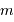 (
(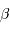 graphiquement, et montrer que
graphiquement, et montrer que 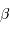 est voisin de 0.6
est voisin de 0.6
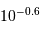 n'est plus vérifiée à grande distance, l'absorption interstellaire et la taille finie de l'épaisseur du bras galactique conduisant à un déficit de magnitudes faibles.
n'est plus vérifiée à grande distance, l'absorption interstellaire et la taille finie de l'épaisseur du bras galactique conduisant à un déficit de magnitudes faibles.
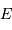 d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
d'une étoile comme la puissance reçue d'une étoile par unité de surface, au
sommet de l'atmosphère terrestre.
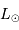 , en
déduire l'éclairement
, en
déduire l'éclairement 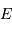 de cette étoile située à une distance
de cette étoile située à une distance 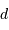 de la Terre.
de la Terre.
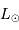 est une puissance et
est une puissance et 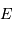 une puissance surfacique
une puissance surfacique
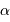 = 0.76". On donne
= 0.76". On donne 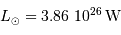 .
.
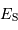 du Soleil reçu sur Terre.
du Soleil reçu sur Terre.
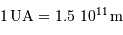
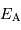 et
et 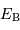 . Exprimer leur différence de magnitude.
. Exprimer leur différence de magnitude.
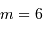 .
.
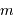 , la magnitude apparente d'un objet :
, la magnitude apparente d'un objet :
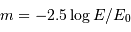
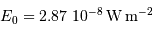 pour le domaine visible.
pour le domaine visible.
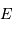 , le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de
, le flux (puissance par unité de surface) rayonné traversant la pupille, en fonction de 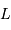 et
et 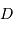 , respectivement la puissance totale reçue et le diamètre de la pupille.
, respectivement la puissance totale reçue et le diamètre de la pupille.
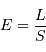
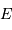 et
et 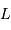 pour une étoile de magnitude 6.
pour une étoile de magnitude 6.
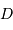 , l'oeil a accès aux magnitudes jusqu'à :
, l'oeil a accès aux magnitudes jusqu'à :
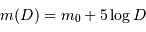
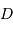 exprimé en m. Identifier
exprimé en m. Identifier 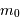
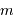 , pour
, pour 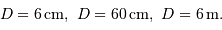
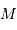 .
.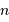 .
.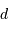 .
.
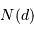 dans une sphère de rayon
dans une sphère de rayon 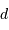 autour du
soleil.
autour du
soleil.
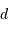 est... allons, un petit effort
est... allons, un petit effort
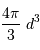
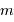 évolue comme :
évolue comme :
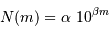
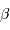 de l'exposant
de l'exposant
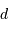 des équations précédentes
des équations précédentes
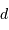 , exprimé en parsec, s'exprime en fonction des magnitudes par
, exprimé en parsec, s'exprime en fonction des magnitudes par
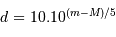
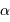 , sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
, sachant que l'on peut dénombrer environ 6000 étoiles à
l'oeil nu, càd de magnitude inférieure à 6.
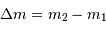 .
Exprimer le rapport de leurs luminosités
.
Exprimer le rapport de leurs luminosités 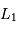 et
et 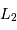
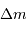 = 1,
= 1, 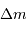 = 10
= 10
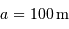 . Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
. Devant l'accumulation de points durs techniques, le concept a été remplacé en 2006 par un projet moins démesuré, avec un collecteur de diamètre 42 m.
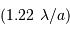 . Calculer cette limite pour le visible.
. Calculer cette limite pour le visible.




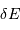 étant divisé selon la longueur d'onde
étant divisé selon la longueur d'onde 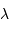 .
.
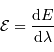
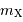 en comparant la densité spectrale de flux
en comparant la densité spectrale de flux 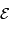 à une référence
à une référence 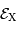 :
:
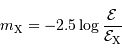
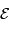 et
et 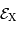 sont exprimés en
sont exprimés en 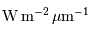 .
.
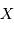
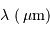
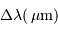
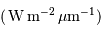
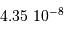
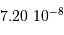
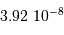
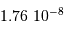
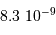
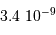
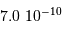
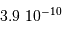
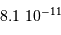
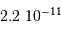
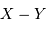 est la différence des magnitudes monochromatiques
est la différence des magnitudes monochromatiques
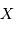 et
et 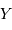 . On codifie la couleur
. On codifie la couleur 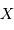 selon le standard UBVRI,
correspondant aux
selon le standard UBVRI,
correspondant aux 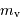
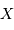 , notée
, notée 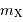 , est reliée à la densité spectrale de flux
, est reliée à la densité spectrale de flux 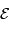 , reçue dans la gamme de couleur
, reçue dans la gamme de couleur 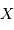 centrée sur la longueur d'onde
centrée sur la longueur d'onde 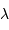 et de largeur
et de largeur 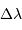 , par :
, par :
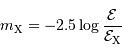
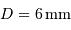 . La magnitude
. La magnitude 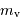 maximum détectable à l'oeil est
maximum détectable à l'oeil est 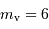
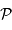 minimale l'oeil est-il sensible ?
minimale l'oeil est-il sensible ?
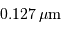 .
.
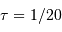 de seconde?
de seconde?
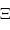 d'un photon de longueur d'onde
d'un photon de longueur d'onde 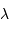 :
:
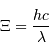
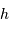 est la constante de Planck
est la constante de Planck 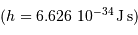 , et
, et 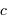 la célérité de la lumière dans le vide.
la célérité de la lumière dans le vide.
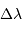 ), avec une chaîne de rendement total
), avec une chaîne de rendement total 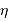 . Ce rendement tient compte de la collecte des photons jusqu'à leur transformation en
. Ce rendement tient compte de la collecte des photons jusqu'à leur transformation en 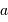 le diamètre collecteur.
le diamètre collecteur.
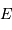 à la magnitude
à la magnitude 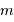 de la source.
Quelles grandeurs de la chaîne de collecte interviennent pour traduire cet éclairement monochromatique en puissance ?
de la source.
Quelles grandeurs de la chaîne de collecte interviennent pour traduire cet éclairement monochromatique en puissance ?
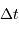 .
.
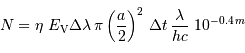
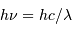 .
.

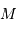 est la magnitude conventionnelle qu'aurait l'étoile si sa distance était ramenée, par définition à 10 pc.
est la magnitude conventionnelle qu'aurait l'étoile si sa distance était ramenée, par définition à 10 pc.
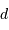 à la Terre,
ce que l'on fait avec
à la Terre,
ce que l'on fait avec 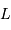 de l'étoile, mesurant la puissance totale
rayonnée par l'étoile :
de l'étoile, mesurant la puissance totale
rayonnée par l'étoile :
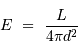
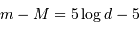
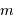
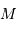
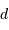 (pc)
(pc)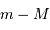 porte le nom de module de distance. En reliant la distance à une différence de magnitude, ce module indique la distance en échelle logarithmique.
porte le nom de module de distance. En reliant la distance à une différence de magnitude, ce module indique la distance en échelle logarithmique.
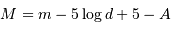
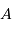 ne peut être que positif ; ne pas en tenir compte conduit à surestimer la magnitude absolue, càd à sous-estimer la luminosité de l'objet.
ne peut être que positif ; ne pas en tenir compte conduit à surestimer la magnitude absolue, càd à sous-estimer la luminosité de l'objet.
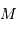 .
.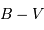 est positif pour un objet plutôt
est positif pour un objet plutôt
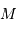 d'un objet. Quelle relation lie la magnitude relative
d'un objet. Quelle relation lie la magnitude relative 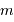 à la magnitude absolue
à la magnitude absolue 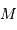 et à la distance
et à la distance 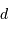 de l'étoile, exprimée en parsec?
de l'étoile, exprimée en parsec?
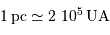
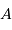 .
.
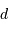 =
20 kpc. Comment est corrigée cette distance si l'on tient compte d'un
coefficient d'absorption de 0.2 magnitude ? Conclure.
=
20 kpc. Comment est corrigée cette distance si l'on tient compte d'un
coefficient d'absorption de 0.2 magnitude ? Conclure.

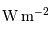
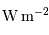
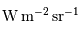
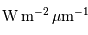
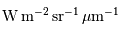
 avec comme unité spectrale la longueur d'onde exprimée en micromètre.
avec comme unité spectrale la longueur d'onde exprimée en micromètre.
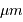 .
.

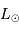 est uniformément répartie sur la sphère de rayon
est uniformément répartie sur la sphère de rayon
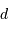 :
:
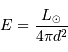
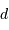 :
:
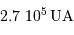 .
.
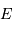 :
:
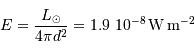
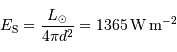
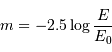
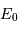 est l'éclairement apparent de référence.
est l'éclairement apparent de référence.
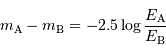
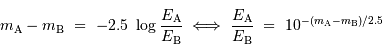
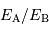 )
)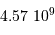
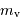 = 6
= 6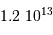
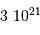
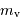 = 6
= 6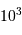
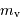 = 6
= 6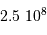
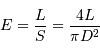
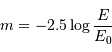 ,
conduit à :
,
conduit à :
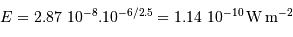
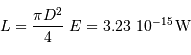
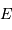 identiquement égal à
identiquement égal à 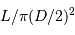 .
.
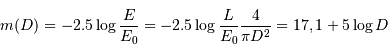
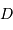
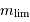
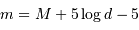
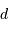 multiplié par la densité stellaire donne le nombre d'étoiles :
multiplié par la densité stellaire donne le nombre d'étoiles :
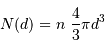
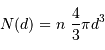 et
et
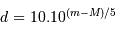 , il sort immédiatement :
, il sort immédiatement :
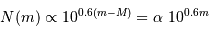
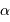 de vérifier :
de vérifier :
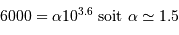
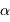 s'identifie à
s'identifie à 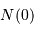 , nombre d'étoiles de magnitude
inférieure à
, nombre d'étoiles de magnitude
inférieure à 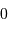 . Si l'on se réfère au
. Si l'on se réfère au
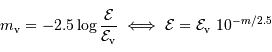
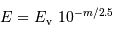
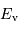 de référence se calcule par:
de référence se calcule par:
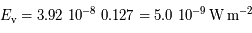
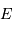 devient alors simplement :
devient alors simplement :
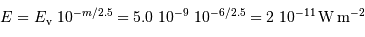
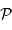 :
:
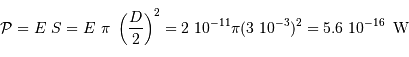
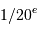 de seconde vaut :
de seconde vaut :
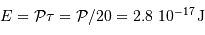
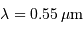 étant:
étant:
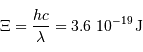
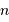 correspond à cette énergie intégrée pendant
correspond à cette énergie intégrée pendant 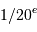 de seconde sur la rétine :
de seconde sur la rétine :
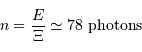
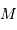 est la magnitude conventionnelle qu'aurait l'étoile si sa distance était égale à 10 pc :
est la magnitude conventionnelle qu'aurait l'étoile si sa distance était égale à 10 pc :
![M = -2.5\log\left[{E\over E _{\mathrm{0}}}.\left({d\over 10}\right)^{2}\right]= -2.5\log {E\over E _{\mathrm{0}}} - 5\log d + 5 \iff](../pages_luminosite/equations_magnitude-absolue/equation19.png)
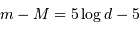
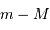 est le module de distance de l'étoile.
est le module de distance de l'étoile.
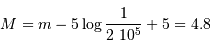
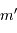 du Soleil s'il était à une distance de 1.33 pc de la Terre :
du Soleil s'il était à une distance de 1.33 pc de la Terre :
![m' = -2.5\log\left[{E\over E _{\mathrm{0}}}\left({d\over 1.33}\right)^{2}\right] = m - 5\log {d\over 1.33} = 0.48](../pages_luminosite/equations_magnitude-absolue/equation25.png)
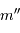 du Soleil s'il était à une distance de 8 kpc de la Terre :
du Soleil s'il était à une distance de 8 kpc de la Terre :
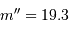
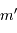 d'une étoile vue à une distance
d'une étoile vue à une distance 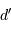 peut s'exprimer ainsi :
peut s'exprimer ainsi :
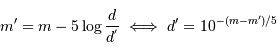
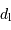 à laquelle une étoile de type solaire reste visible à l'oeil nu est :
à laquelle une étoile de type solaire reste visible à l'oeil nu est :