En savoir plus: La définition des éléments elliptiques-2

En savoir plus

Les formules du problème des deux corps permettent de calculer la position de l'astre sur son orbite pour un instant t quelconque.

L'anomalie moyenne M (parfois notée l dans le cas de la Lune) est donnée par M = n.(t - t₀) où n est le moyen mouvement.

Le moyen mouvement n est lié au demi-grand axe a de l'ellipse par la troisième loi de Kepler (n²a³ = constante).

On passe de l'anomalie moyenne M à l'anomalie excentrique E en résolvant l'équation de Kepler : E - e sin E = M. Cette équation se résout par itérations successives.

E_0=M

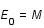
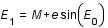
E_1=M+e*sin(E_0)

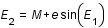
E_2=M+e*sin(E_1)

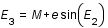E_3=M+e*sin(E_2) et ainsi de suite.

Enfin, connaissant l'anomalie excentrique E, l'anomalie vraie v et le rayon vecteur r sont donnés par les équations suivantes :

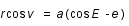
r*cos(v) =a*(cos(E) - e)

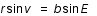
r*sin(v)=b*sin(E)

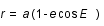
r=a*(1 - e*cos(E))

Le plan de l'orbite n'étant pas a priori dans le plan de l'écliptique, ces deux plans se coupent suivant une droite appelée ligne des noeuds ligne des noeuds. Cette ligne des noeuds coupe l'orbite du corps en deux points : le noeud ascendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes négatives aux latitudes positives et le noeud descendant de l'orbite par lequel passe le corps lorsqu'il passe des latitudes positives aux latitudes négatives.