
|
On s'intéresse à différents temps caractéristiques d'un nuage de matière protostellaire. Le temps de chute libre mesure la durée caractéristique de l'accrétion d'un nuage ; le temps de Kelvin-Helmholtz mesure la durée maximale pendant laquelle un objet peut rayonner par simple contraction gravitationnelle.
En supposant que le nuage s'effondre sans rencontrer de résistance, le temps de chute libre correspond à la durée d'effondrement sous l'effet de l'autogravitation du nuage. Le nuage parcourt son rayon sous son propre champ gravitationnel en une durée 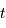 vérifiant :
vérifiant :
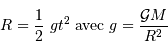
Pour un corps autogravitant de masse 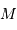 et rayon
et rayon 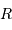 , l'analyse dimensionnelle impose :
, l'analyse dimensionnelle impose :
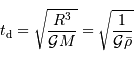
où 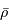 est la masse volumique moyenne du corps.
Comme l'on considère seulement l'interaction gravitationnelle, en négligeant toute résistance, la température du nuage ne joue aucun rôle. En fonction de la densité particulaire, le temps de chute libre s'exprime :
est la masse volumique moyenne du corps.
Comme l'on considère seulement l'interaction gravitationnelle, en négligeant toute résistance, la température du nuage ne joue aucun rôle. En fonction de la densité particulaire, le temps de chute libre s'exprime :
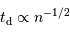
La contraction d'un nuage s'accompagne, d'après le théorème du viriel d'une puissance rayonnée correspondant au taux de variation de l'énergie potentielle d'interaction gravitationnelle :
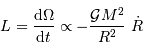
La phase de luminosité uniquement due à la contraction gravitationnelle peut se poursuivre sur une durée, appelée temps de Kelvin-Helmholtz, définie par le rapport :
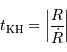
En fonction de ce qui précède, on en déduit que cette constante de temps caractéristique s'exprime :
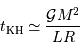
Elle augmente avec la masse (le réservoir d'énergie) et diminue avec la puissance rayonnée (la perte d'énergie).
Pour le Soleil (avec une puissance rayonnée 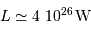 et les masse et rayon actuels) la constante de temps est de l'ordre de 30 millions d'années. Ceci signifie que, par simple contraction gravitationnelle, le Soleil peut rayonner pendant cette durée, sans autre source d'énergie.
et les masse et rayon actuels) la constante de temps est de l'ordre de 30 millions d'années. Ceci signifie que, par simple contraction gravitationnelle, le Soleil peut rayonner pendant cette durée, sans autre source d'énergie.