Apprendre

Objectifs

Par rapport au modèle d'effondrement purement mécanique, il faut tenir compte du rayonnement de la proto-étoile qui s'effondre et s'échauffe. Le théorème du viriel montre que la moitié seulement de l'énergie gagnée par l'effondrement est convertie en énergie thermique, l'autre moitié est directement rayonnée par l'objet condensé qui se réchauffe.

Conservation de l'énergie

Le modèle étudié précédemment suppose, à juste titre, la conservation de l'énergie, mais à tort que toute cette énergie est sous forme mécanique. Le milieu qui se densifie s'échauffe, et rayonne de l'énergie.

Energie rayonnée

Le théorème du viriel, ici accepté, énonce que l'énergie interne thermique ne représente que la moitié de l'énergie interne gravitationnelle : un bilan énergétique de l'évolution vers un état à l'équilibre hydrostatique implique que la moitié de l'énergie interne est évacuée par radiation.

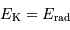Lors de la formation d'une étoile, il y a échauffement et obligatoirement perte d'énergie par radiation, à parts égales : $E _{\mathrm{K}} = E _{\mathrm{rad}}$ .

Conséquence du théorème du viriel

On peut donc réécrire la loi de conservation de l'énergie :

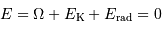
$E = \Omega + E _{\mathrm{K}} + E _{\mathrm{rad}} = 0$

Avec l'égalité entre les énergies rayonnée et cinétique :

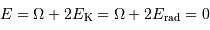
$E = \Omega + 2 E _{\mathrm{K}} = \Omega + 2 E _{\mathrm{rad}} = 0$

Ceci conduit à une estimation de la température interne de moitié moindre à celle obtenue en omettant l'énergie rayonnée.

Puissance rayonnée

La luminosité de l'étoile est reliée au taux de variation de l'énergie rayonnée :

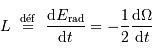
$L \ \stackrel{\mathrm{d\acute ef}}{=}\ { {\mathrm{d}} E _{\mathrm{rad}} \over {\mathrm{d}} t} = -{1\over 2} { {\mathrm{d}} \Omega \over {\mathrm{d}} t}$

Il s'ensuite que :

Une proto-étoile brille déjà, avant même d'avoir allumé ses réactions nucléaires.
Entre 2 états à l'équilibre hydrostatique, une contraction du rayon implique une perte d'énergie par radiation.

Remarques

De manière plus générale, à tout champ de force correspond une forme particulière du viriel. Pour un champ linéaire (de type ressort), énergies potentielle et cinétique moyennes sont égales. Pour un champ newtonien, elles sont respectivement dans un rapport -2.