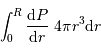 |  |  |  |  |  |
|
Démonstration du théorème du viriel, dans un cas simplement modéliséDifficulté : ☆☆☆ Temps : 1 h
Cet exercice a pour but d'établir le théorème du viriel, dans un cas simple. On suppose qu'à tout instant, l'astre, sous forme déjà condensée de rayon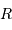 
, obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
Dans le cadre du modèle, avec les notations du cours, on écrit l'énergie cinétique comme une intégrale :
.
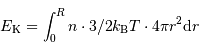Réécrire cette intégrale en fonction de la pression.
L'équilibre hydrostatique énonce que le gradient de la pression évolue comme :
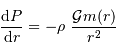
Montrer, à l'aide de cette égalité, que l'énergie gravitationnelle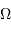 
peut s'écrire sous la forme d'une intégrale du gradient de la pression.
Estimer le lien entre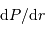 
et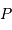 
en procédant à l'intégration par parties du terme :
 |  |
S'exercer
, on introduit simplement la pression, pour obtenir :
au rayon 
:
:
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation23.png)
).
et 
.
