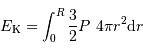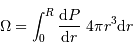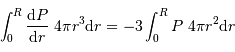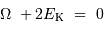Différents éléments physiques sont introduits, qui vont conduire à comprendre dans quelles conditions fonctionne une étoile, et à montrer le rôle crucial de la gravitation.
C'est la masse de l'étoile qui pilote son évolution, mais il n'y a pas incohérence avec le plan total du cours ; on entre dans un domaine où la masse, si elle conditionne l'essentiel, n'explique pas tout. On est bien... dans le chapitre Température.

La nébuleuse de la Tête de Cheval, dans la constellation d'Orion à 1500 AL du Soleil, regroupe les différents ingrédients intervenant lors de la genèse stellaire : région dense de gaz et de poussières, région d'hydrogène ionisé HII, étoiles en cours de formation.
Crédit :
ESO
 Prérequis
Prérequis
Éléments de théorie cinétique du gaz parfait.
Gaz parfait 
Gaz parfait
Rappel : un gaz est dit parfait si les interactions entre particules se réduisent à des chocs élastiques.
Pour un gaz parfait usuel, non dégénéré (c'est à dire non soumis à des effets quantique) et classique (c'est à dire non relativiste), l'équation d'état s'écrit :
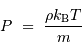
avec 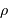 la masse volumique, et
la masse volumique, et 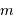 la masse d'une particule élémentaire du gaz.
la masse d'une particule élémentaire du gaz.
Un gaz parfait est dit chaud s'il est dominé par l'agitation thermique. Les effets quantiques sont dans ce cas négligeables.
Un gaz parfait est dit froid lorsque les effets thermiques ne
jouent plus aucun rôle. Son incompressibilité provient du
tassement de la matière : les cortèges électroniques se repoussent
en raison de la nature quantique (fermionique) des électrons.
Température
Pour que la température d'un système soit définie, il faut que ce système soit à l'équilibre, et que ses composantes échangent assez d'informations, via des collisions, pour se thermaliser.
Dans un milieu non collisionnel, il y a peu de chances que l'on puisse définir une température qui vaille... mais on ne s'intéresse pas la suite qu'à des milieux à l'équilibre thermodynamique local, où localement la température est bien définie.
Densité particulaire
La densité particulaire est une grandeur couramment utilisée pour mesurer l'abondance de matériau disponible dans un milieu. Elle est comptée en particules (souvent des électrons, ou des atomes ou molécules d'hydrogène) par unité de volume. Par exemple : 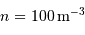 .
.
Autogravitation et forme sphérique
Une étoile présente une forme sphérique, pas évidente à voir vu la petitesse du rayon stellaire devant la distance entre elle et le Soleil. Le disque stellaire d'une étoile ne peut être imagé que si cette étoile est une géante du proche voisinage solaire.
Un noyau de comète, tel celui de la comète de Halley, n'est pas assez massif pour être façonné par sa propre gravitation. Sa forme n'est pas sphérique.
Atmosphère de Bételgeuse

Atmosphère de l'étoile supergéante rouge Bételgeuse. Cette géante
rouge, de diamètre 800 fois celui du Soleil, est suffisamment
proche (130 pc) pour que son disque puisse être imagé.
Crédit :
HST
Noyau de la comète de Halley

Noyau de la comète de Halley, vue en 1986 par la sonde européenne Giotto, lors d'un survol à 600 km (mais avec une vitesse relative de 70 km/s. Ce noyau cométaire n'est pas assez massif pour acquérir une forme sphérique.
Crédit :
ESA
 Objectifs
Objectifs
Exprimer sous forme d'une pression (la pression centrale) l'autogravitation d'une étoile.
Autogravitation
On qualifie d'autogravitant un objet soumis à sa propre gravitation et façonné par elle. Le Soleil, la Terre sont des objets autogravitants. Toi, lecteur, tu n'es pas un objet auto-gravitant (tout au plus sujet à un peu d'embonpoint).
Rien n'interdit à un objet autogravitant de graviter autour d'un autre astre, comme la Terre autour du Soleil ou la Lune autour de la Terre.
Un objet autogravitant est de forme sphérique si sa rotation propre n'est pas trop importante, ou ovoïde aplatie dans le cas contraire.
Équilibre
Comme cette pression rend compte de l'interaction gravitationnelle, attractive, on l'appellera par la suite compression. Il va falloir lui trouver, au sein d'un astre, une contrepartie répulsive pour assurer l'équilibre d'une étoile.
Rotation et aplatissement
La rotation de Saturne est suffisamment rapide pour conduire à un aplatissement sensible.
Le mesurer à l'aide de l'appliquette ci-contre, en déterminant le rapport 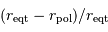 .
.
Montrer que l'inclinaison sous laquelle on voit la planète, estimée à partir des anneaux, ne perturbe pas significativement la mesure précédente.
Saturne 
 Compression gravitationnelle
Compression gravitationnelle
Difficulté : ☆☆☆
Temps : 30 min
Le but de l'exercice est d'estimer la constante de proportionnalité de la compression gravitationnelle. Pour dépasser l'approximation d'une masse volumique uniforme, et rendre compte d'une distribution de masse volumique plus piquée vers le centre, tout en gardant des calculs acceptablement légers, on suppose le modèle suivant :
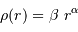 .
.
On s'intéresse à des exposants légèrement négatifs, conduisant à une singularité au centre, qui ne prête pas à conséquence.
Question 1)
Déterminer la relation entre la masse totale 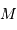 et le rayon extérieur
et le rayon extérieur 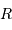 . En déduire l'expression du coefficient
. En déduire l'expression du coefficient 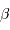 en fonction de ces grandeurs.
en fonction de ces grandeurs.
[2 points]
Pour cette distribution sphérique :
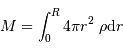
Question 2)
En déduire la masse 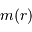 et le champ gravitationnel en un point de rayon
et le champ gravitationnel en un point de rayon 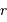 . Quelle condition sur l'exposant
. Quelle condition sur l'exposant 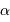 garantit que le champ ne diverge pas ?
garantit que le champ ne diverge pas ?
[2 points]
Pour des calculs plus simples, on écrit :
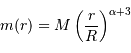
Par définition :
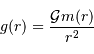
Question 3)
L'équilibre hydrostatique donne le gradient de pression :
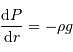
En déduire la pression centrale.
[2 points]
Mener le calcul, du centre vers la surface :
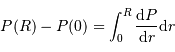
Question 4)
Discuter de la forme du résultat précédent. Que se passe-t-il pour une distribution uniforme ?
[1 points]
Traduire l'uniformité de la masse volumique sur l'exposant 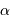 .
.
Est-il normal de retrouver 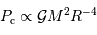 ?
?
 Ainsi fond, fond, fond...
Ainsi fond, fond, fond...
Difficulté : ☆☆
Temps : 30 min
Limbe lunaire : la hauteur des plus hauts reliefs reste petite devant le rayon.

Relief sur le limbe lunaire.
Crédit :
ASM
Le but de cet exercice est de modéliser la hauteur limite d'une montagne sur une planète de masse 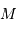 et rayon
et rayon 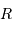 , pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
On suppose très hardiment la montagne de forme cylindrique, section 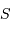 et hauteur
et hauteur 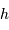 , dans le champ gravitationnel uniforme de la planète.
, dans le champ gravitationnel uniforme de la planète.
Question 2)
En déduire la valeur limite de la hauteur 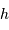 , pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 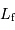 . Faire l'application numérique pour la Terre, avec
. Faire l'application numérique pour la Terre, avec 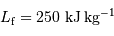 .
.
[2 points]
Comparer les énergies en jeu.
Question 3)
Les plus hautes montagnes atteignent 8.8 km sur Terre (l'Everest) et 27 sur Mars (le Mont Olympe). A l'aide des données du calcotron, vérifier si l'estimation précédente est correcte.
[1 points]
Question 4)
En supposant toujours valable le résultat précédent, et en notant 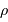 la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 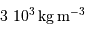 .
.
[2 points]
Ne pas se laisser désarçonner par les hypothèses, qui restent en ordre de grandeur très convenables.
 Prérequis
Prérequis
Notion de gaz parfait.
 Objectifs
Objectifs
Une étoile peut exister sous réserve d'être dans un état d'équilibre. La compression d'origine gravitationnelle, qui tend à condenser l'étoile, doit être balancée par une autre source de pression : pression cinétique (ou thermique), pression de dégénérescence (ou quantique), pression de rayonnement.
Pression cinétique
Aussi appelée pression thermique, cette pression est celle du gaz parfait chaud. Dans le cas classique, non relativiste, cette pression s'exprime pour un gaz de masse volumique
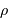 à la température
à la température 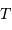 , composé de particules de masse
, composé de particules de masse 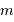 :
:
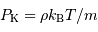
En fonction de la densité particulaire 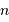 , la définition devient :
, la définition devient :
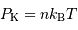
Pression de dégénérescence, ou pression de Fermi, ou pression quantique
La pression de dégénérescence est la pression dans un gaz parfait dit froid. Dans un milieu froid ou dense, les termes cinétiques peuvent devenir négligeables et les interactions entre nuages électroniques des atomes présents prépondérantes. La pression est alors dominée par la pression de dégénérescence 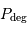 des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
La pression de dégénérescence s'écrit alors (dans le cas non relativiste) :
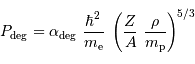
avec 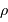 la masse volumique, et
la masse volumique, et 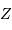 et
et 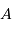 respectivement la charge et le nombre de masse des atomes en présence. La constante
respectivement la charge et le nombre de masse des atomes en présence. La constante 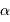 est un nombre : le calcul précis donne
est un nombre : le calcul précis donne 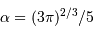 .
.
Dans certains cas, tel l'intérieur d'une étoile à neutrons, il peut ne plus y avoir d'électrons pour assurer la pression. On trouve alors des neutrons, qui sont toujours des fermions, et la pression de dégénérescence des neutrons s'écrit :
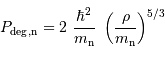
Quel terme de pression domine en fonction de la température ?
La nature est complexe, si bien que ce qui suit n'est pas toujours vrai, mais en général :
- Dans un milieu dense et froid, c'est la pression de dégénérescence qui domine. Ex : au centre de la Terre d'une planète, ou d'une étoile de masse inférieure à 1 masse solaire.
- Dans un milieu plus chaud, la pression cinétique mène la danse. Par exemple : au centre d'une étoile telle le Soleil ou plus massive. La pression de dégénérescence intervient dans les stades ultimes de l'évolution stellaire.
- Ce n'est qu'aux températures extrêmes atteinte au centre des étoiles les plus massives que la pression de radiation l'emporte.
Supporter la gravitation
Dans tous les cas, l'un des 3 termes de pression, ou l'association de 2 d'entre eux, doit permettre d'équilibrer la compression gravitationnelle.
Si, on le verra plus loin, la source énergétique essentielle pour l'étoile adulte, dans la séquence principale, est l'énergie nucléaire, c'est la gravitation qui pilote l'évolution stellaire via la masse de l'objet.

 Pression de Fermi
Pression de Fermi
Difficulté : ☆☆☆
Temps : 60 min
Cet exercice a pour but d'expliciter l'expression de la pression de Fermi, qui s'exerce lorsque la nature fermionique des composants est mise en évidence. Comme il s'agit de physique complexe, ce sont seulement les ordres de grandeur qui sont importants.
Question 1)
Rappeler la relation d'incertitude de Heisenberg entre la position 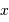 d'une particule sur un axe et sa quantité de mouvement
d'une particule sur un axe et sa quantité de mouvement 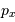 .
.
[1 points]
Question 2)
Relier l'incertitude de position 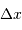 à la densité particulaire
à la densité particulaire 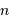 .
.
[1 points]
Faire le lien entre la densité particulaire 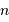 et le volume moyen par particule.
et le volume moyen par particule.
S'intéresser à l'encombrement au sein du gaz, en estimant qu'une particule occupe un volume de l'ordre de 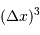 .
.
Question 3)
Montrer que, pour un gaz avec une distribution de vitesse typique, maxwellienne, la distribution de vitesse donne une valeur moyenne et une largeur de distribution du même ordre de grandeur.
[1 points]
La distribution de vitesse maxwellienne varie comme
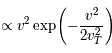 avec
avec 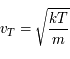
Question 4)
On rappelle que la pression est un flux de quantité de mouvement
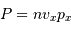
De ce qui précède (en admettant aussi que 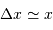 ), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
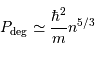
[2 points]
Pour un gaz classique : 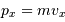 .
.
Éliminer des relations précédentes les variables de quantité de mouvement et de position au profit de la densité particulaire.
Question 5)
Montrer que la pression électronique domine par rapport à la pression des protons.
[1 points]
Comparer les masses en jeu.
Question 6)
En déduire l'expression de la pression de dégénérescence donnée dans le
cours.
[1 points]
Se servir de la neutralité électrique.
L'essentiel de la masse se retrouve dans les nucléons.

Amas Messier 35 et NGC2158. Tous deux sont des amas ouverts, mais l'un, âgé de 100 millions d'années, présente beaucoup d'étoiles jeunes, lorsque, 6 fois plus distant et 10 fois plus âgé, ne peut plus contenir d'étoiles jeunes.
Crédit :
CFHT
Système lié
L'observation de groupes stellaires formant apparemment un
système lié semble indiquer une origine commune. L'estimation des
énergies cinétique et potentielle permet d'estimer l'énergie
mécanique totale. Si les termes cinétiques dominent, l'amas est
ouvert.
 Objectifs
Objectifs
Mesurer l'énergie que représente l'accrétion d'un corps dense.
Analyse dimensionnelle
On s'intéresse à un corps autogravitant de masse 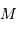 et rayon
et rayon 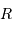 . Quelle énergie peut-on lui associer de par sa gravitation ?
. Quelle énergie peut-on lui associer de par sa gravitation ?
L'analyse dimensionnelle apporte une première réponse à cette question. Avec les caractéristiques de l'objet et la constante gravitationnelle 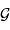 :
:
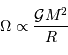
Pour s'en convaincre, il suffit de revenir à la définition de l'interaction gravitationnelle.
Énergie potentielle d'interaction gravitationnelle
Avec un peu de physique, on peut se convaincre d'un supplément d'information :
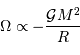
L'interaction en jeu étant attractive, nécessairement l'énergie associée à un corps dense est négative : en effet, pour défaire ce corps, il faudrait lui fournir un travail positif, pour éparpiller très loin chacune de ses particules.
L'énergie potentielle d'interaction gravitationnelle d'un objet est d'autant plus négative qu'il est massif et/ou condensé.
Le calcul complet de cette énergie potentielle est proposé en exercice.
 Calcul de l'énergie potentielle
Calcul de l'énergie potentielle
Difficulté : ☆☆☆
Temps : 45 min
Cet exercice un peu technique s'adresse surtout aux étudiants en licence ou maîtrise scientifique ; sinon, se contenter de suivre l'approche qualitative.
L'exercice s'attelle à la construction d'un objet stellaire. On part de rien. On y met un chouïa de matière, puis un peu plus, puis encore plus, jusqu'à constituer un corps de rayon 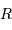 et masse
et masse 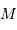 . Dans cette modélisation, on suppose qu'à tout moment la masse volumique
. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 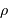 est uniforme.
est uniforme.
Question 1)
On imagine être à une étape intermédiaire caractérisée par un rayon 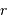 et une masse
et une masse 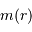 . Déterminer cette masse, ainsi que son champ gravitationnel.
. Déterminer cette masse, ainsi que son champ gravitationnel.
[2 points]
Rappel : la masse volumique est supposée uniforme.
Question 2)
Déterminer le travail d'un opérateur qui amènerait un surcroît de
masse 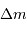 depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
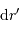 ):
):
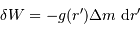
[2 points]
Le travail total est la somme des contributions des travaux de l'infini à la surface de l'objet
Question 4)
En déduire le travail total pour créer le corps, somme de toutes les contributions.
[2 points]
IC1396 en infrarouge

Nuage interstellaire (dans la nébuleuse IC1396), d'apparence bien développée dans le proche infrarouge, hébergeant de nombreuses étoiles en formation. L'aspect filamentaire provient des effets d'érosion du vent stellaire d'une étoile massive (hors champ, sur la gauche du cliché).
Crédit :
NASA/Spitzer
IC1396 en lumière visible

Même région qu'à la
figure
précédente, mais en lumière visible et non infrarouge.
On y distingue les résidus du nuage interstellaire ayant conduit à
une genèse stellaire. En effet, en lumière visible, les régions
les plus denses du nuage apparaissent totalement obscures, ou
réfléchissant le rayonnement intense des étoiles jeunes
nouvellement formées.
Crédit :
NASA/Spitzer
Contraste
Le milieu interstellaire montre des régions de matière très froide (typiquement 10 K) et très peu dense (quelques particules 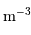 ), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement
), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement 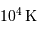 en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement
en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement 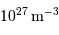 ).
).
Comble du contraste : les étoiles jeunes se situent au sein de ces régions, ou ce qu'il en reste dès lors que le rayonnement de l'étoile parvient à percer.
Etat initial
On suppose le nuage initialement très peu dense et très froid. Il ne possède ni énergie cinétique (il est trop froid), ni énergie potentielle d'interaction (la matière est beaucoup trop diluée). On résume la situation par une énergie mécanique totale quasi nulle (plus précisément : ces énergies sont initialement totalement négligeables par rapport aux énergies cinétiques et potentielles à venir) :
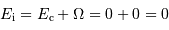
Etat final
Dans un état condensé, l'énergie cinétique qui relate l'agitation thermique n'est plus négligeable. Si 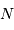 atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de
atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de 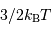 par nucléon :
par nucléon :
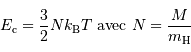
L'énergie potentielle rend compte de la très énergique interaction gravitationnelle des 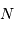 atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours
atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours 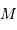 la masse concernée, et
la masse concernée, et 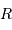 le rayon final de l'objet condensé.
le rayon final de l'objet condensé.
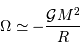
L'énergie totale s'exprime alors :
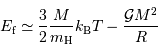
Effondrement et échauffement
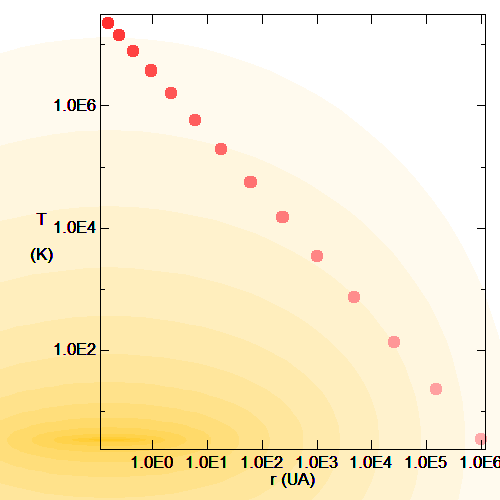
Lorsque le nuage se contracte, il se réchauffe.
Crédit :
ASM
Et la rotation ?
La conservation du moment cinétique et les collisions entre particules conduit à aplatir le système. En effet, par suite des collisions, les composantes de vitesse parallèles au moment cinétique vont peu à peu s'annuler, en gardant une valeur moyenne nulle, quand les vitesses perpendiculaires se thermalisent. Ceci est traité plus en détail à la page consacrée aux disques d'accrétion.
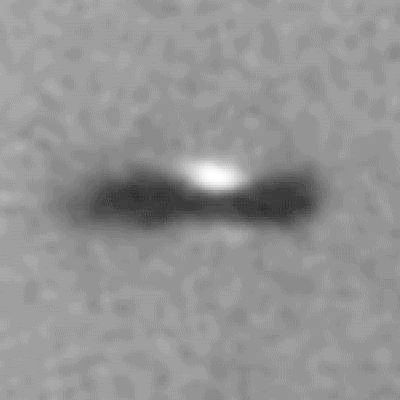
Disque protoplanétaire dans la constellation d'Orion. Au centre du nuage, l'élévation de température conduit à un objet brillant qui commence à rayonner.
Crédit :
HST
Fiat lux
La contraction du nuage l'échauffe en son centre, et donc la proto-étoile se met à rayonner. De l'énergie, initialement sous forme uniquement mécanique, a été convertie en énergie lumineuse.
 Objectifs
Objectifs
Par rapport au modèle d'effondrement purement mécanique, il faut tenir compte du rayonnement de la proto-étoile qui s'effondre et s'échauffe. Le théorème du viriel montre que la moitié seulement de l'énergie gagnée par l'effondrement est convertie en énergie thermique, l'autre moitié est directement rayonnée par l'objet condensé qui se réchauffe.
Conservation de l'énergie
Le modèle étudié précédemment suppose, à juste titre, la conservation de l'énergie, mais à tort que toute cette énergie est sous forme mécanique. Le milieu qui se densifie s'échauffe, et rayonne de l'énergie.
Energie rayonnée
Le théorème du viriel, ici accepté, énonce que l'énergie interne thermique ne représente que la moitié de l'énergie
interne gravitationnelle : un bilan énergétique de l'évolution vers un état à
l'équilibre hydrostatique implique que la moitié de l'énergie interne est évacuée par radiation.
Lors de la formation d'une étoile, il y a échauffement et
obligatoirement perte d'énergie par radiation, à parts égales :
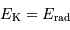 .
.
Conséquence du théorème du viriel
On peut donc réécrire la loi de conservation de l'énergie :
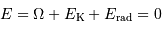
Avec l'égalité entre les énergies rayonnée et cinétique :
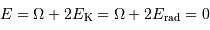
Ceci conduit à une estimation de la température interne de moitié moindre à celle obtenue en omettant l'énergie rayonnée.
Puissance rayonnée
La luminosité de l'étoile est reliée au taux de variation de l'énergie rayonnée :
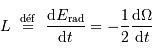
Il s'ensuite que :
- Une proto-étoile brille déjà, avant même d'avoir allumé ses réactions nucléaires.
- Entre 2 états à l'équilibre hydrostatique, une contraction du rayon implique une perte d'énergie par radiation.
Remarques
De manière plus générale, à tout champ de force correspond une forme particulière du viriel.
Pour un champ linéaire (de type ressort), énergies potentielle et cinétique moyennes sont égales. Pour un champ newtonien, elles sont respectivement dans un rapport -2.
 Démonstration du théorème du viriel, dans un cas simplement modélisé
Démonstration du théorème du viriel, dans un cas simplement modélisé
Difficulté : ☆☆☆
Temps : 1 h
Cet exercice a pour but d'établir le théorème du viriel, dans un cas simple. On suppose qu'à tout instant, l'astre, sous forme déjà condensée de rayon 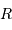 , obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
, obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
Question 1)
Dans le cadre du modèle, avec les notations du cours, on écrit l'énergie cinétique comme une intégrale :
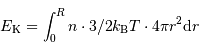 .
Réécrire cette intégrale en fonction de la pression.
.
Réécrire cette intégrale en fonction de la pression.
[1 points]
Il suffit d'introduire l'équation d'état du gaz parfait chaud.
Question 2)
L'équilibre hydrostatique énonce que le gradient de la pression évolue comme :
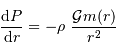
Montrer, à l'aide de cette égalité, que l'énergie gravitationnelle 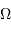 peut s'écrire sous la forme d'une intégrale du gradient de la pression.
peut s'écrire sous la forme d'une intégrale du gradient de la pression.
[3 points]
On peut par exemple commencer par écrire l'énergie potentielle sous forme intégrale
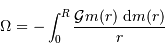
Question 3)
Estimer le lien entre 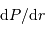 et
et 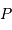 en procédant à l'intégration par parties du terme :
en procédant à l'intégration par parties du terme :
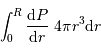
[2 points]
L'intégration par parties donne
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
Montrer que l'un des 2 termes de l'intégration par parties est nul.
Question 4)
En déduire l'égalité vérifiée entre 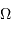 et
et 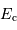 .
.
[2 points]
Tout le travail est fait, il n'y a plus qu'à comparer.
 Energie d'accrétion
Energie d'accrétion
Difficulté : ☆☆
Temps : 20 min
Le but de cet exercice est d'estimer le rayonnement d'une planète géante encore en train de se contracter. On supposera, dans le cas d'un objet de masse volumique uniforme. L'énergie potentielle est :
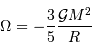
Question 1)
Relier la luminosité de l'objet à sa vitesse de contraction.
[2 points]
La vitesse de contraction est 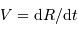 .
.
Par définition, 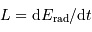 .
.
Le théorème du viriel donne , 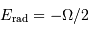 .
.
Question 2)
Quelle puissance rayonne une planète comme Jupiter qui se contracterait de 1 mm/an ? On donne : 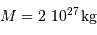 et
et 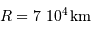 . Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de
. Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de 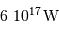 .
.
[1 points]
- Question 1
Aide :
Pour cette distribution sphérique :
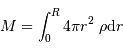
Solution :
Par application de la définition de la masse totale :
![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
Si 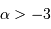 , alors :
, alors :
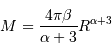
D'où l'expression demandée :
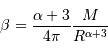
- Question 2
Aide :
Pour des calculs plus simples, on écrit :
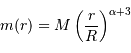
Aide :
Par définition :
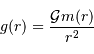
Solution :
De l'expression de la masse totale trouvée précédemment, on peut déduire de la même façon :
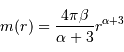
(seule la borne d'intégration supérieure a changé). On en déduit :
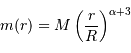
Ensuite, la définition du champ gravitationnel donne :
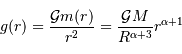
Il semble nécessaire d'avoir un exposant 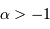 , afin d'éviter que le champ ne diverge au centre.
, afin d'éviter que le champ ne diverge au centre.
- Question 3
Aide :
Mener le calcul, du centre vers la surface :
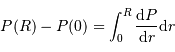
Solution :
On cherche à intégrer la pression du centre 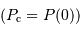 vers la surface
vers la surface 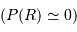 :
:
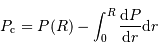
On suppose la pression de surface totalement négligeable. Il reste alors, en fonction de ce qui précède :
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
L'expression du champ a conduit à la restriction 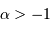 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
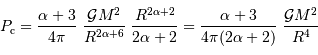
- Question 4
Aide :
Traduire l'uniformité de la masse volumique sur l'exposant 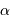 .
.
Aide :
Est-il normal de retrouver 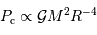 ?
?
Solution :
Retrouver 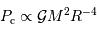 est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 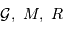 .
.
Si la masse volumique est uniforme, c'est à dire si 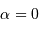 , on trouve :
, on trouve :
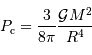
Si la masse volumique pointe vers le centre, c'est àdire 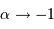 , on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la partie cours, dans le cas du Soleil.
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la partie cours, dans le cas du Soleil.
- Question 1
Solution :
La relation de Heisenberg s'écrit, en notant 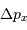 et
et 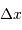 les incertitudes respectives.
les incertitudes respectives.
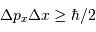
Pour la suite, on considèrera le cas
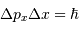
- Question 2
Aide :
Faire le lien entre la densité particulaire 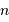 et le volume moyen par particule.
et le volume moyen par particule.
Aide :
S'intéresser à l'encombrement au sein du gaz, en estimant qu'une particule occupe un volume de l'ordre de 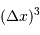 .
.
Solution :
Une densité particulaire 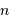 correspond à un volume par particule
correspond à un volume par particule 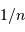 .
Ce volume par particule est lui-même de l'ordre de
.
Ce volume par particule est lui-même de l'ordre de 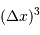 . On en déduit :
. On en déduit :
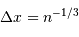
- Question 3
Aide :
La distribution de vitesse maxwellienne varie comme
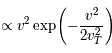 avec
avec 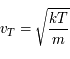
Aide :
Faire un schéma.
Solution :
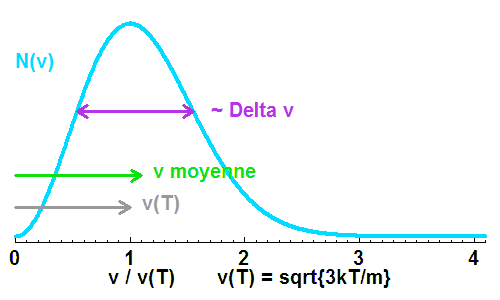
Distribution de vitesse maxwellienne.
Crédit :
ASM
L'examen de la figure montre que vitesse moyenne et écart-type sont du même ordre de grandeur. On confond donc 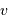 et
et 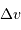 .
.
- Question 4
Aide :
Pour un gaz classique : 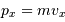 .
.
Aide :
Éliminer des relations précédentes les variables de quantité de mouvement et de position au profit de la densité particulaire.
Solution :
Pour un gaz classique, la quantité de mouvement s'écrit 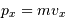 .
.
De 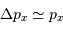 et
et 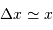 on tire :
on tire :
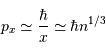
Puis
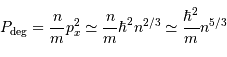
- Question 5
Aide :
Comparer les masses en jeu.
Solution :
Comme le rapport des masses entre le proton et l'électron vaut 2000, s'il y a des électrons, la pression électronique domine largement.
- Question 6
Aide :
Se servir de la neutralité électrique.
Aide :
L'essentiel de la masse se retrouve dans les nucléons.
Solution :
La neutralité électrique assure 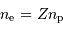 .
.
L'essentiel de la masse se retrouve dans les nucléons : 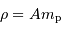 .
.
On retrouve alors le résultat du cours.
- Question 1
Aide :
Rappel : la masse volumique est supposée uniforme.
Solution :
Par définition :
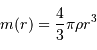
Le champ gravitationnel créé par cette masse à une distance 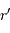 vaut :
vaut :
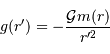
Le signe négatif rend compte de l'attraction gravitationnelle, et il faut bien distinguer les variables 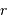 , rayon actuel de l'objet en cours de formation, et
, rayon actuel de l'objet en cours de formation, et 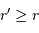 , distance à cet objet.
, distance à cet objet.
- Question 2
Aide :
Le travail total est la somme des contributions des travaux de l'infini à la surface de l'objet
Solution :
À partir d'une étape élémentaire, on somme pour obtenir le travail
total :
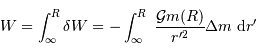
L'intégration donne :
![W = + \left[ { {\cal G} m(M) \over r'}\ \Delta m \right]_\infty^R](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation20.png)
On en tire
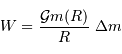
Le travail de l'opérateur est l'opposé de la variation d'énergie potentielle de l'objet entre les 2 états considérés.
- Question 3
Aide :
2 moyens de procéder au calcul, en interprétant l'usage de la notation différentielle, ou bien en raisonnant géométriquement.
Aide :
L'usage de la notation différentielle doit permettre de passer de 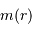 à
à 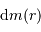 .
.
Solution :
L'accroissement de la masse 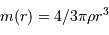 s'écrit par différentiation :
s'écrit par différentiation :
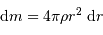
on y reconnaît la masse d'une coquille d'épaisseur 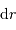 et de surface
et de surface 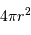 .
.
On a donc :
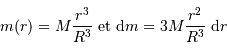
- Question 4
Solution :
De l'expression du travail élémentaire qui précède, on tire l'expression de la variation d'énergie potentielle d'interaction gravitationnelle sur une étape élémentaire :
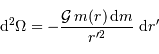
Avec 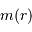 la masse accrétée au rayon
la masse accrétée au rayon 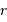 et
et 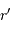 une position entre
une position entre 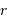 et
et 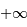 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 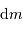 de l'infini à la surface :
de l'infini à la surface :
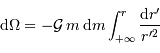
Le calcul de l'intégrale donne ![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
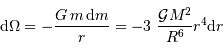
après avoir remplacé 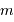 et
et 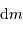 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)
On retrouve ce résultat classique. L'expression est homogène ; le signe négatif rappelle que la formation d'une concentration de matière a dégagé de l'énergie (ou qu'il faut en dépenser pour démonter l'objet).
- Question 1
Aide :
Il suffit d'introduire l'équation d'état du gaz parfait chaud.
Solution :
Avec l'équation d'état du gaz parfait 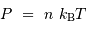 , on introduit simplement la pression, pour obtenir :
, on introduit simplement la pression, pour obtenir :
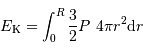
- Question 2
Aide :
On peut par exemple commencer par écrire l'énergie potentielle sous forme intégrale
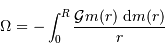
Aide :
On a aussi besoin de la définition de la masse d'une coquille d'épaisseur 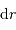 au rayon
au rayon 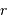 :
:
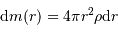
Solution :
La définition de l'énergie potentielle est :
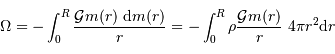
On introduit le gradient de pression, via ce que donne l'équilibre
hydrostatique, sans oublier au passage que 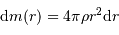 :
:
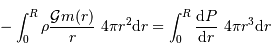
On en déduit :
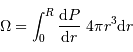
- Question 3
Aide :
L'intégration par parties donne
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
Aide :
Montrer que l'un des 2 termes de l'intégration par parties est nul.
Solution :
Par parties :
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation23.png)
Le terme tout intégré est nul, car nul aux 2 bornes (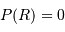 ).
).
- Question 4
Aide :
Tout le travail est fait, il n'y a plus qu'à comparer.
Solution :
On a vu pour l'énergie cinétique :
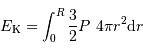
Et pour l'énergie potentielle :
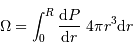
L'égalité trouvée précédemment :
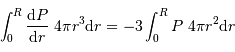
conduit alors à :
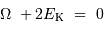
On retrouve donc le théorème du viriel dans un cas particulier.


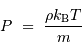
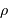 la masse volumique, et
la masse volumique, et 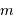 la masse d'une particule élémentaire du gaz.
la masse d'une particule élémentaire du gaz.
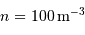 .
.
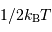 par degré de liberté. L'énergie cinétique de translation vaut
par degré de liberté. L'énergie cinétique de translation vaut 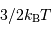 . Pour une collection de
. Pour une collection de 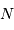 particules, l'énergie cinétique totale se monte tout simplement à
particules, l'énergie cinétique totale se monte tout simplement à 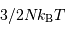 .
.
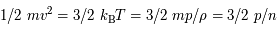 .
avec
.
avec 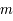 la masse d'une particule et
la masse d'une particule et 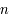 la densité particulaire. On en déduit :
la densité particulaire. On en déduit :
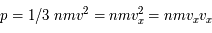 avec
avec 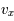 la composante de la vitesse selon un seul axe (le milieu étant supposé homogène et isotrope :
la composante de la vitesse selon un seul axe (le milieu étant supposé homogène et isotrope : 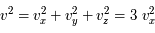 . On retrouve bien le flux de quantité de mouvement
. On retrouve bien le flux de quantité de mouvement 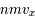 .
.


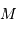 et rayon
et rayon 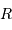 . Elle vaut :
. Elle vaut :
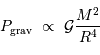
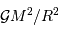 étant homogène à une force.
étant homogène à une force.
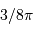 ; comme vérifié en
; comme vérifié en 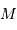 (kg)
(kg)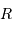 (km)
(km) 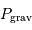 (Pa)
(Pa)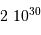
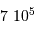
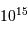
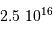
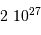
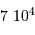
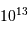
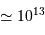
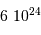
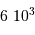
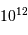
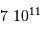
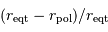 .
.
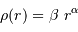 .
.
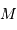 et le rayon extérieur
et le rayon extérieur 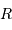 . En déduire l'expression du coefficient
. En déduire l'expression du coefficient 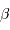 en fonction de ces grandeurs.
en fonction de ces grandeurs.
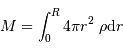
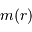 et le champ gravitationnel en un point de rayon
et le champ gravitationnel en un point de rayon 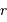 . Quelle condition sur l'exposant
. Quelle condition sur l'exposant 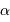 garantit que le champ ne diverge pas ?
garantit que le champ ne diverge pas ?
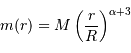
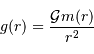
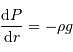
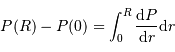
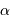 .
.
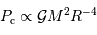 ?
?

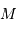 et rayon
et rayon 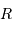 , pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
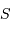 et hauteur
et hauteur 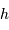 , dans le champ gravitationnel uniforme de la planète.
, dans le champ gravitationnel uniforme de la planète.
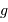 . Déterminer l'énergie supplémentaire pour rajouter au sommet une masse
. Déterminer l'énergie supplémentaire pour rajouter au sommet une masse 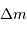 , en fonction de
, en fonction de 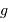 et
et 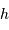 .
.
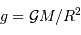 .
.
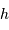 , pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 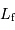 . Faire l'application numérique pour la Terre, avec
. Faire l'application numérique pour la Terre, avec 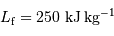 .
.
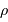 la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 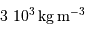 .
.
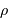 à la température
à la température 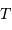 , composé de particules de masse
, composé de particules de masse 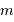 :
:
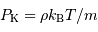
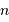 , la définition devient :
, la définition devient :
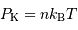
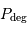 des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
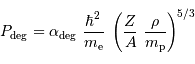
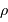 la masse volumique, et
la masse volumique, et 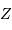 et
et 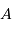 respectivement la charge et le nombre de masse des atomes en présence. La constante
respectivement la charge et le nombre de masse des atomes en présence. La constante 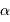 est un nombre : le calcul précis donne
est un nombre : le calcul précis donne 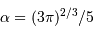 .
.
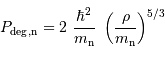
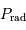 du gaz de photons à la température
du gaz de photons à la température 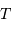 s'exprime par :
s'exprime par :
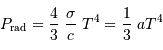
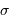 est la constante de Stefan-Boltzmann :
est la constante de Stefan-Boltzmann :
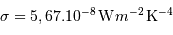 .
La grandeur
.
La grandeur 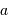 s'écrit :
s'écrit :
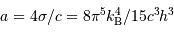 . En unité SI,
. En unité SI, 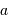 vaut
vaut
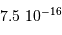 . La dépendance de cette pression avec la puissance quatrième de la température est bien sûr reliée au spectre du
. La dépendance de cette pression avec la puissance quatrième de la température est bien sûr reliée au spectre du 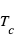 centrale (en million de Kelvin) et de la masse volumique
centrale (en million de Kelvin) et de la masse volumique 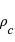 centrale (en unité
centrale (en unité 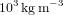 ). Le but de la simulation est d'estimer le terme de pression dominant au centre de l'étoile, en fonction de sa masse. On mènera les calculs avec des pressions exprimées en unité 1 Gbar (1 milliard de fois la pression atmosphérique, soit
). Le but de la simulation est d'estimer le terme de pression dominant au centre de l'étoile, en fonction de sa masse. On mènera les calculs avec des pressions exprimées en unité 1 Gbar (1 milliard de fois la pression atmosphérique, soit 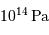 ).
).
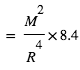 ] pour avoir la bonne unité
] pour avoir la bonne unité
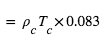 ]
]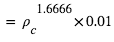 ]
]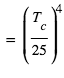 ]
]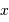 d'une particule sur un axe et sa quantité de mouvement
d'une particule sur un axe et sa quantité de mouvement 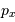 .
.
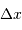 à la densité particulaire
à la densité particulaire 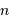 .
.
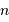 et le volume moyen par particule.
et le volume moyen par particule.
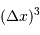 .
.
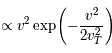 avec
avec 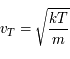
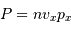
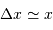 ), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
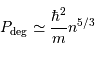
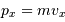 .
.

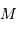 et rayon
et rayon 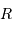 . Quelle énergie peut-on lui associer de par sa gravitation ?
. Quelle énergie peut-on lui associer de par sa gravitation ?
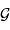 :
:
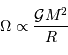
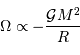
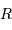 et masse
et masse 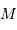 . Dans cette modélisation, on suppose qu'à tout moment la masse volumique
. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 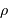 est uniforme.
est uniforme.
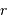 et une masse
et une masse 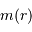 . Déterminer cette masse, ainsi que son champ gravitationnel.
. Déterminer cette masse, ainsi que son champ gravitationnel.
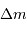 depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
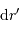 ):
):
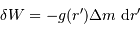
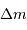 sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon
sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon 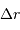 . Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle
. Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle 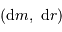 . Exprimer alors
. Exprimer alors 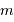 et
et 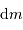 en fonction de la masse totale finale
en fonction de la masse totale finale 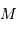 , des rayons
, des rayons 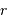 et
et 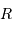 , et l'accroissement
, et l'accroissement 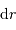 .
.
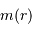 à
à 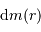 .
.


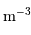 ), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement
), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement 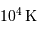 en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement
en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement 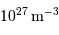 ).
).
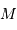 de gaz conduisant à un corps condensé de rayon
de gaz conduisant à un corps condensé de rayon 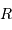 donne une température centrale variant comme
donne une température centrale variant comme 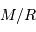 , d'autant plus élevée que le corps est massif et dense.
, d'autant plus élevée que le corps est massif et dense.
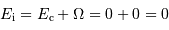
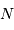 atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de
atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de 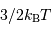 par nucléon :
par nucléon :
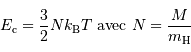
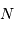 atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours
atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours 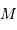 la masse concernée, et
la masse concernée, et 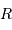 le rayon final de l'objet condensé.
le rayon final de l'objet condensé.
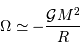
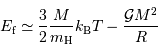

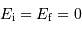
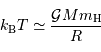
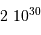
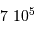
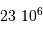
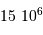
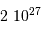
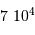
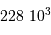
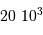
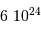
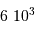
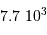
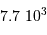

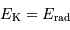 .
.
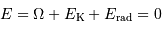
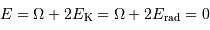
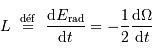
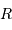 , obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
, obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
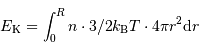 .
Réécrire cette intégrale en fonction de la pression.
.
Réécrire cette intégrale en fonction de la pression.
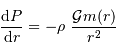
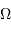 peut s'écrire sous la forme d'une intégrale du gradient de la pression.
peut s'écrire sous la forme d'une intégrale du gradient de la pression.
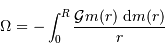
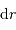 au rayon
au rayon 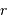 :
:
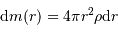
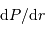 et
et 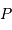 en procédant à l'intégration par parties du terme :
en procédant à l'intégration par parties du terme :
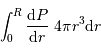
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
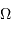 et
et 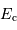 .
.
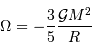
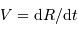 .
.
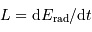 .
.
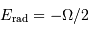 .
.
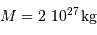 et
et 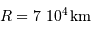 . Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de
. Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de 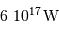 .
.
![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
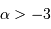 , alors :
, alors :
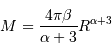
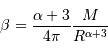
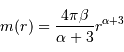
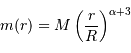
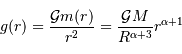
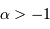 , afin d'éviter que le champ ne diverge au centre.
, afin d'éviter que le champ ne diverge au centre.
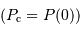 vers la surface
vers la surface 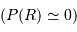 :
:
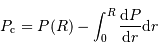
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
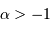 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
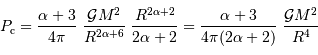
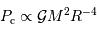 est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 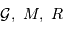 .
.
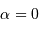 , on trouve :
, on trouve :
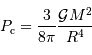
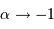 , on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la 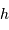 la masse considérée coûte en énergie, dans le champ
la masse considérée coûte en énergie, dans le champ 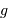 supposé uniforme :
supposé uniforme :
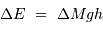
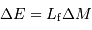 , et donc si :
, et donc si :
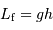
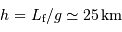
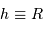 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
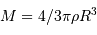 conduisent à :
conduisent à :
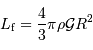
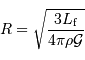
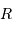 de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
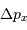 et
et 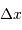 les incertitudes respectives.
les incertitudes respectives.
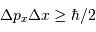
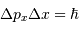
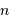 correspond à un volume par particule
correspond à un volume par particule 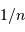 .
Ce volume par particule est lui-même de l'ordre de
.
Ce volume par particule est lui-même de l'ordre de 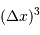 . On en déduit :
. On en déduit :
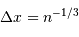

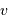 et
et 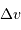 .
.
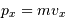 .
.
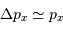 et
et 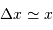 on tire :
on tire :
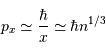
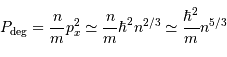
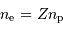 .
.
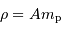 .
.
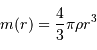
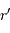 vaut :
vaut :
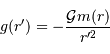
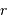 , rayon actuel de l'objet en cours de formation, et
, rayon actuel de l'objet en cours de formation, et 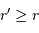 , distance à cet objet.
, distance à cet objet.
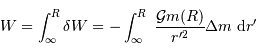
![W = + \left[ { {\cal G} m(M) \over r'}\ \Delta m \right]_\infty^R](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation20.png)
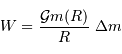
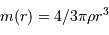 s'écrit par différentiation :
s'écrit par différentiation :
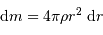
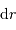 et de surface
et de surface 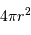 .
.
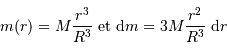
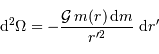
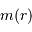 la masse accrétée au rayon
la masse accrétée au rayon 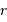 et
et 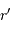 une position entre
une position entre 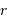 et
et 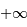 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 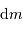 de l'infini à la surface :
de l'infini à la surface :
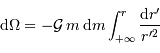
![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
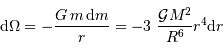
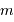 et
et 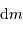 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)
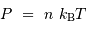 , on introduit simplement la pression, pour obtenir :
, on introduit simplement la pression, pour obtenir :
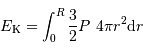
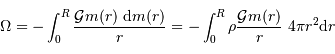
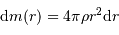 :
:
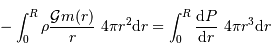
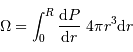
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation23.png)
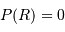 ).
).