Comprendre
Auteurs: Thomas Navarro, Arianna Piccialli
- La circulation atmosphérique générale
- Outils
- Coordonnées sphériques
- Forces apparentes
- Force centrifuge
- Force de Coriolis
- Formalisme eulérien ou lagrangien
- Équations de la dynamique
- Les équations primitives
- Les équilibres dynamiques
- Équilibre géostrophique
- Équilibre cyclostrophique
- Nombre de Rossby
- Nombre de Rossby
- Systemes géostrophiques
- Systemes cyclostrophiques
- Instabilités
- Ondes atmosphériques
- Caractéristiques des ondes
- Onde sonore
- Exemples d'ondes atmosphériques
La circulation atmosphérique générale
Auteurs: Thomas Navarro, Arianna Piccialli
Outils
Auteurs: Thomas Navarro, Arianna Piccialli
Coordonnées sphériques
Comme toute équation de la physique, les équations régissant la dynamique atmosphérique doivent s'exprimer dans un système de coordonnées et un référentiel choisis arbitrairement. Un tel système naturellement adapté à une sphère, et donc à une planète, sont les coordonnées sphériques 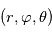 , où
, où 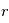 est la distance au centre de la sphère,
est la distance au centre de la sphère, 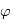 est la l'angle de la longitude, et
est la l'angle de la longitude, et 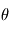 est l'angle de la latitude.
est l'angle de la latitude.
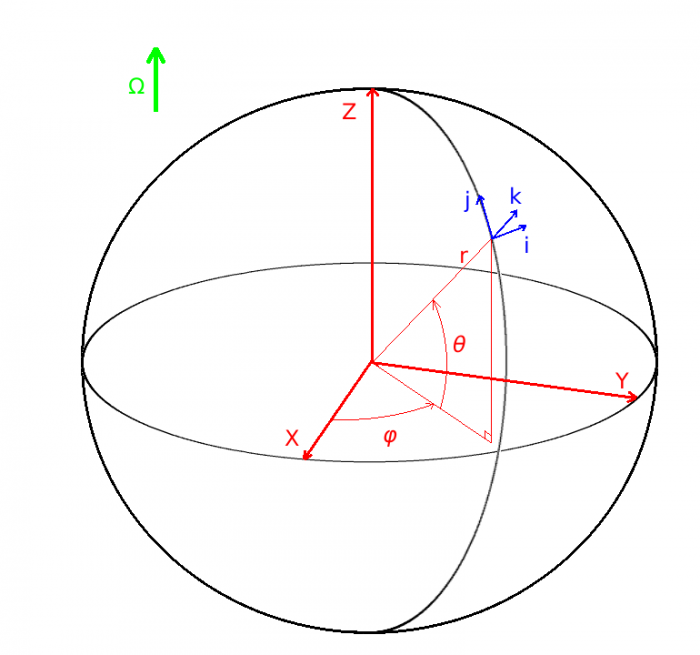
On définit également un repère local pour tout point de l'espace de coordonnées 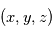 , avec comme base le triplet
, avec comme base le triplet 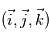 où
où 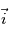 est dirigé vers l'Est,
est dirigé vers l'Est, 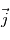 dirigé vers le Nord, et
dirigé vers le Nord, et 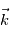 selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
Système de coordonnées sphériques
Crédit :
Arianna Piccialli
L'exercice suivant permet de se familiariser avec la manipulation mathématique des coordonnées et des repères. Les resultats serviront à établir l'équation fondamentale de la dynamique.
 Exercice
Exercice
Question 1)
Montrer que dans le référentiel de la planète, un point de coordonnées sphériques 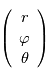 a pour coordonnées cartésiennes
a pour coordonnées cartésiennes 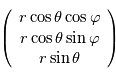
Question 3)
Montrer qu'une vitesse dans le référentiel local 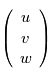 au point de coordonnées sphériques
au point de coordonnées sphériques 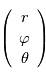 s'exprime par
s'exprime par 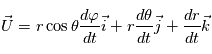 .
.
Forces apparentes
Pour résoudre les équations régissant une atmosphère, on se place dans le référentiel local, lui-même dans un référentiel tournant avec la planète. Ce référentiel n'est pas inertiel, c'est-à-dire qu'il est en accélération par rapport à un référentiel inertiel. Afin de poser le principe fondamental de la dynamique, il est essentiel de tenir de compte de l'accélération apparente du référentiel d'étude, sous la forme de pseudo-forces.
 Précision
Précision
Traditionnellement et pour des raisons pratiques on parle de force, ou pseudo-force, en multipliant l'accélération apparente par la masse de l'objet. On parlera ici plutôt de l'accélération d'une force apparente afin de s'affranchir du terme de masse, qui disparaitra dans les équations finales.
Force centrifuge
 Force centrifuge
Force centrifuge
La force centrifuge est la force apparente due au fait que le référentiel d'étude est en rotation, donc en accélération. En effet, l'orientation de la vitesse d'un point lié à la planète varie, mais pas son module. Ainsi, une particule au repos dans un référentiel galiléen aura une force apparente dans le référentiel de la planète.
On définit le vecteur rotation 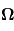 comme étant le vecteur orienté selon l'axe de rotation de la planète et de module
comme étant le vecteur orienté selon l'axe de rotation de la planète et de module 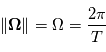 avec
avec 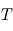 la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime
la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime 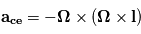 avec
avec 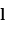 le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a
le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a 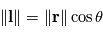 , avec
, avec 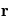 le vecteur position depuis le centre de la planète.
le vecteur position depuis le centre de la planète.
Une autre manière de l'exprimer est de dire qu'il s'agit d'une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur 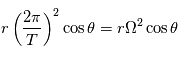
La force centrifuge est regroupée avec la force de gravité, dont l'accélération vaut 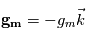 , l'indice
, l'indice 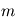 faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est
faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est 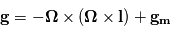 . Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
. Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
 Exercices de démonstration et d'acquisition du cours
Exercices de démonstration et d'acquisition du cours
Question 1)
Démontrer par l'analyse ou par un schéma en 3D que 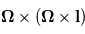 correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur
correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur 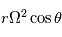 . Comment s'exprime cette accélération dans le référentiel local ?
. Comment s'exprime cette accélération dans le référentiel local ?
Question 2)
Par la suite on fait l'approximation que l'accélération due au géopotentiel est orientée selon l'axe 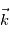 . Quelle erreur est faite pour la Terre ? pour Jupiter ?
. Quelle erreur est faite pour la Terre ? pour Jupiter ?
Force de Coriolis
Dans un référentiel en rotation, une autre force apparente est à prendre en compte lors d'un déplacement. Il s'agit de la force de Coriolis, qui tient compte du fait que le déplacement d'une particule génère une accélération apparente supplémentaire. Par exemple, le mouvement rectiligne d'une particule est apparement dévié pour un observateur situé dans un référentiel tournant.
L'accélération de la force de Coriolis s'exprime 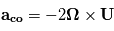 avec
avec 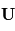 le vecteur vitesse de la parcelle d'air considérée.
le vecteur vitesse de la parcelle d'air considérée.
La vitesse 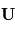 d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en général petite par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en général petite par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
- A l'équateur l'accélération de Coriolis est orientée selon l'axe radial, c'est-à-dire vers le haut ou vers le bas.
- Dans l'hémisphère Nord, sa projection sur le plan de la surface locale est orientée à droite du vecteur vitesse
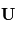
- Dans l'hémisphère Sud, sa projection sur le plan de la surface locale est orientée à gauche du vecteur vitesse
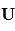
Ceci explique pourquoi certaines structures atmosphériques, tels les ouragans ou les anticyclones, tournent toujours dans le sens des aiguilles d'une montre dans l'hémisphère Nord, et dans le sens contraire dans l'autre hémisphère.
 Exercice de démonstration et d'acquisition du cours
Exercice de démonstration et d'acquisition du cours
Question 1)
Démontrer par l'analyse ou par un schéma en 3D les 3 points ci-dessus.
Formalisme eulérien ou lagrangien
Les écoulements atmosphériques peuvent être décrits en utilisant deux points de vue classiques, appelés eulérien ou lagrangien :
 Description eulérienne
Description eulérienne
L'écoulement est suivi par un observateur depuis une position fixe. C'est le cas, par exemple, d'un atterrisseur sur Mars fixé au sol qui mesure la vitesse du vent, la température, ou la pression. Cette description est souvent préférée car elle est la plus pratique.
 Description lagrangienne
Description lagrangienne
Dans ce cas, les particules fluides sont suivies le long de leurs trajectoires. C'est la description la plus intuitive.
Équations de la dynamique
 Exercice
Exercice
Question 1)
Comment s'exprime l'accélération de la force de Coriolis 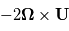 dans le repère local ?
dans le repère local ?
C'est le même exercice que celui sur la force de Coriolis, mais sans négliger la composante 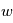 .
.
 Exercice
Exercice
Question 1)
Déduire les équations de Navier-Stokes en coordonnées sphériques à partir de l'équation fondamentale de la dynamique (Equation 1).
Les équations primitives
 Approximations
Approximations
Les équations de la dynamique sont très compliquées car elles forment un système non linéaire. Ceci signifie que la somme de deux solutions n'est pas forcément solution du problème, ce qui rend la résolution de ces équations très ardue, et à ce jour encore source de recherches. Cependant, en fonction des phénomènes étudiés et des caractéristiques de l'atmosphère planétaire, certains termes de ces équations peuvent en dominer d'autres. Pour estimer les différents termes dans les équations, on utilise la méthode de l'analyse d'échelle. Les ordres de grandeur des différents termes en jeu dans les équations fondamentales de la dynamique seront très différents selon l'échelle des écoulements que l'on souhaite étudier. Dans le tableau ci-dessous on compare les termes dominants sur les planètes à rotation rapide (la Terre) avec ceux sur les planètes à rotation lente (Vénus):
Termes dominants dans les équations de la dynamique
| 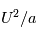 | 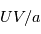 | 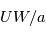 | 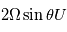 | 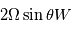 | 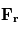 |
| Terre | 10-5 | 10-5 | 10-8 | 10-3 | 10-6 | 10-12 |
| Vénus | 10-3 | 10-5 | 10-5 | 10-5 | 10-7 | 10-12 |
avec 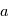 le rayon de la planète. On a
le rayon de la planète. On a 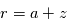 , où
, où 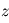 est l'altitude depuis la surface.
est l'altitude depuis la surface.
On peut alors appliquer les approximations suivantes:
- L'épaisseur verticale de l'atmosphère est petite par rapport au le rayon de la planète. Par conséquence, on remplace la distance
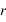 au centre de la planète par le rayon de la planète
au centre de la planète par le rayon de la planète 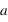 avec une erreur négligeable. Dans ce cas, les dérivées
avec une erreur négligeable. Dans ce cas, les dérivées 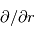 deviennent
deviennent 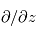 où
où 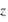 est l'altitude.
est l'altitude. - Les trois composantes du terme de friction moléculaire
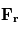 ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol.
ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol. - Les vitesses verticales sont beaucoup plus petites que les vitesses horizontales, donc on néglige tous les termes contenant
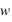 .
. - Dans le cas de mouvements à grande échelle, on suppose l'équilibre hydrostatique :
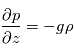
On obtient alors les équations primitives de la météorologie :
 Equilibre hydrostatique vertical:
Equilibre hydrostatique vertical:
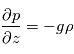
À ce système d'équations on ajoute l'équation des gaz parfaits:
ainsi que l'équation de conservation de la masse:
 Equation de continuité:
Equation de continuité:
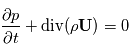
Enfin, le premier principe de la thermodynamique:
On obtient ainsi 6 équations avec 6 inconnues (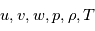 ).
).
Ce système d'équations primitives est le plus complet utilisé pour l'étude de la circulation générale de l'atmosphère. C'est notamment celui utilisé par les modèles de circulation générale.
Les équilibres dynamiques
Équilibre géostrophique
Les équilibres géostrophique et cyclostrophique sont deux approximations des équations primitives. Ils sont purement diagnostiques : ils ne contiennent pas de dérivées dans le temps, d'où l'impossibilité de faire des prédictions. Néanmoins, ils sont des outils puissants pour décrire différents écoulements observés dans les planètes.
 L'équilibre géostrophique
L'équilibre géostrophique
L'approximation géostrophique est un développement des équations primitives utilisée aux moyennes latitudes sur les planètes à rotation rapide (Terre, Mars). On suppose l'équilibre entre la force de Coriolis et la force due au gradient horizontal de pression. La force centrifuge est négligée.
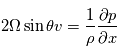
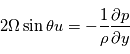
D'après ces équations, lorsque cet équilibre est valide, la vitesse du vent est directement proportionnelle au gradient horizontal de pression. Notez que l'équilibre géostrophique cesse d'être valide autour des latitudes équatoriales.
Force en action en équilibre géostrophique
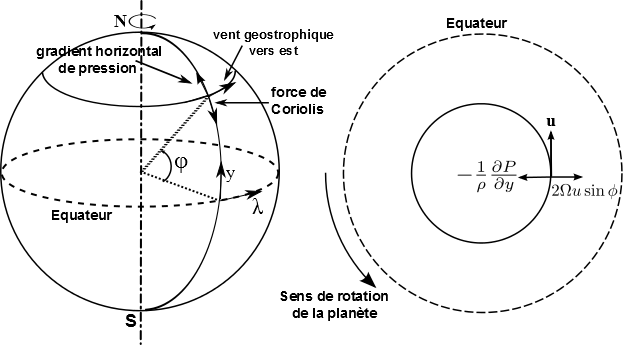
Crédit :
Arianna Piccialli
 Vent géostrophique
Vent géostrophique
En combinant les deux composantes de la vitesse, on peut introduir le vent géostrophique comme :
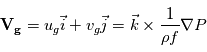
Équilibre cyclostrophique
 L'équilibre cyclostrophique
L'équilibre cyclostrophique
La circulation générale des planètes à rotation lente (Vénus, Titan), aussi bien que les vortex et les tourbillons sur toutes les planètes, peut être approximée par l'équilibre cyclostrophique. Cela suppose l'égalité entre la composante dirigée vers l'équateur de la force centrifuge et le gradient méridional de la pression. La force de Coriolis est négligée.
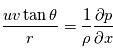
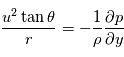
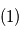
Forces en action en équilibre cyclostrophique
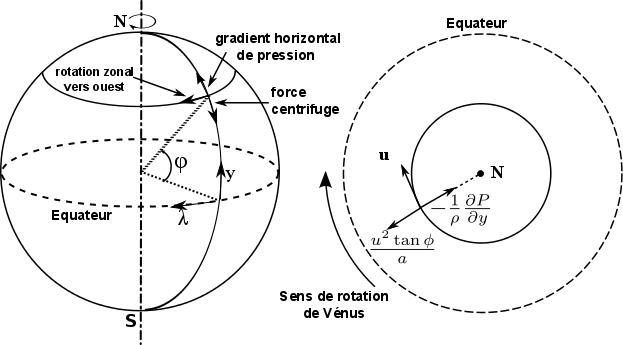
Crédit :
Arianna Piccialli, adaptation de Schubert, 1983.
 Vent cyclostrophique
Vent cyclostrophique
L'équation du vent cyclostrophique peut alors être écrite comme :
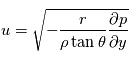
 Exercice
Exercice
Nombre de Rossby
Auteurs: Thomas Navarro, Arianna Piccialli
Nombre de Rossby
 Définition
Définition
Le nombre de Rossby est un nombre sans dimension qui permet de caractériser les mouvements atmosphériques. Il est défini par:
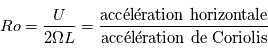
où 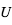 est une vitesse caractéristique du système,
est une vitesse caractéristique du système, 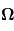 est la vitesse angulaire de rotation de la planète, et
est la vitesse angulaire de rotation de la planète, et 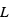 est une longueur caractéristique du système.
est une longueur caractéristique du système.
 Exercice
Exercice
Question 1)
Quelle est la dimension du nombre de Rossby ?
Une valeur de nombre de Rossby très supérieure à l'unité indique que la force de Coriolis due à la rotation de la planète est négligeable par rapport à la force d'inertie, dans ce cas on parle d'équilibre cyclostrophique. Dans le cas contraire d'un nombre de Rossby inférieur à l'unité, l'équilibre est dit géostrophique.
Les équilibres dynamiques
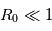 | Equilibre géostrophique | [Terre, Mars] |
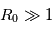 | Equilibre cyclostrophique | [Vénus, Titan, Ouragans] |
Systemes géostrophiques
 La Terre et Mars
La Terre et Mars
La Terre et Mars présentent une circulation atmosphérique aux grandes échelles très similaire et typique des planètes à rotation rapide : les deux planètes ont en fait une période de rotation similaire (Voir Tableau). La principale différence entre eux vient de:
- La présence d'océans sur la Terre.
- Le cycle de CO2 sur Mars, qui produit la condensation/sublimation d'une grande masse de CO2.
Un régime géostrophique des vents zonaux domine la circulation dans les deux planètes en dehors des latitudes tropicales. Aux latitudes moyennes, à la fois sur la Terre et sur Mars, la circulation est caractérisée par deux courant-jets, un dans chaque hémisphère.
Sur la Terre, ces jets sont des vents zonaux qui circulent de l'ouest vers l'est et leur vitesse augmente avec l'altitude jusqu'à la tropopause. Au-dessus de la tropopause ces jets affaiblissent, et puis ils augmentent encore avec l'altitude au-dessus de 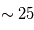 km jusqu'à
km jusqu'à 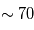 km, où ils atteignent une vitesse de 60 m s-1.
km, où ils atteignent une vitesse de 60 m s-1.
Sur Mars, en raison de l'atmosphère très ténue et de l'absence des océans, l'atmosphère réagit presque instantanément au chauffage solaire. C'est aussi la raison pour laquelle les courant-jets dépendent des variations saisonnières. Au solstice d'hiver dans l'hémisphère nord, le courant-jet est centré entre 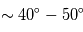 de latitude atteignant une vitesse maximale de 40 m s-1 à 5 km. Il augmente encore à 35 km, où il atteint une vitesse de 110 m s-1. A cette même époque, le courant-jet dans l'hémisphère sud est beaucoup plus faible.
de latitude atteignant une vitesse maximale de 40 m s-1 à 5 km. Il augmente encore à 35 km, où il atteint une vitesse de 110 m s-1. A cette même époque, le courant-jet dans l'hémisphère sud est beaucoup plus faible.
Il faut noter que ces configurations des vents sont une moyenne temporelle et spatiale et ils sont vus rarement sur des journées individuelles. Les configurations des vents d'un jour à l'autre dévient considérablement de cette circulation globale.
Systemes cyclostrophiques
 Vénus et Titan
Vénus et Titan
Vénus et Titan sont deux planètes à rotation lente, caractérisées respectivement par une période de rotation de 244 jours (Vénus) et 16 jours (Titan). Une description détaillée de leur circulation peut être trouvée ici. Les deux planètes sont caractérisées par des forts vents zonaux dans l'ensemble de l'atmosphère, une caractéristique appelée super-rotation. Sur Vénus, la super-rotation atteint une vitesse supérieure à 100 m s-1 au sommet des nuages (vers 70 km d'altitude), correspondant à une période de rotation de 4 jours terrestres (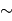 60 fois plus rapide que Vénus elle-même).
Différentes études ont montré que sur les planètes qui tournent lentement, comme Vénus et Titan, les forts vents zonaux au sommet des nuages peuvent être décrits par l’équilibre cyclostrophique. Ce qui donne une possibilité de reconstruire le vent zonal si le champ de température est connu.
60 fois plus rapide que Vénus elle-même).
Différentes études ont montré que sur les planètes qui tournent lentement, comme Vénus et Titan, les forts vents zonaux au sommet des nuages peuvent être décrits par l’équilibre cyclostrophique. Ce qui donne une possibilité de reconstruire le vent zonal si le champ de température est connu.
 Tornades et ouragans sur la Terre
Tornades et ouragans sur la Terre
D'autres systèmes cyclostrophiques à petite échelle sont les ouragans et les tornades (Figure 1); ils sont caractérisés par un centre de basse pression et de forts vents. En raison d'un nombre de Rossby élevé (Tableau 1), la force de Coriolis peut être négligée pour les tornades et les ouragans, et on suppose l'équilibre entre la force centrifuge et le gradient de pression.
Figure 1

Une tornade sur Terre observé par l'équipe VORTEX-99 le 3 Mai 1999 en Oklahoma.
Crédit :
National Oceanic and Atmospheric Administration (NOAA).
Selon le glossaire de météorologie (AMS 2000), une tornade est une colonne d'air tournant violemment, en contact avec le sol et la base des nuages, et souvent (mais pas toujours) visible comme un nuage en forme d'entonnoir (Figure 1). La plupart des tornades ont des vitesses de vent entre 18 m s-1 et 135 m s-1. Son vortex a un diamètre typique de quelques centaines de mètres et tourne, en général, dans le sens contraire des aiguilles d'une montre dans l'hémisphère Nord. Les tornades se produisent sur tous les continents, mais sont plus fréquentes dans les États-Unis, où le nombre moyen de tornades enregistrées est d'environ 1000 par an, avec la majorité d'entre eux sur les plaines centrales et dans les états du sud. Les tornades sont associées à des orages violents et sont alimentés par l'afflux d'air chaud et humide. En général, ils sont le résultat de l'instabilité produit par la différence de température et d'humidité entre la surface, où l'air est plus chaud, et les niveaux supérieurs de l'orage, où l'air est plus froid.
Ouragan est le nom utilisé pour indiquer les cyclones tropicaux qui se produisent dans l'Atlantique ou le Pacifique Est. Les ouragans sont marqués par une région centrale d'air descendants, l'oeil, enfermé par des orages forts associés à des vents et des pluies intenses. Comme pour le cas des tornades, l'énergie des ouragans est fournie principalement par libération de chaleur latente dans l'air humide. Les ouragans sur la Terre se forment dans les régions tropicales au-dessus des océans chauds, et ils s'affaiblissent lorsqu'ils arrivent sur terre, où la source d'énergie disparaît. Dans l'oeil d'un ouragan, le nombre de Rossby locale est toujours 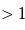 et peut arriver jusqu'à 100. Dans ce cas, l'équilibre devient cyclostrophique.
et peut arriver jusqu'à 100. Dans ce cas, l'équilibre devient cyclostrophique.
Les cyclones tropicaux sur la Terre et le vortex polaire de Vénus présentent des similitudes morphologiques et dynamiques, comme on peut voir dans la Figure 2. Le vortex de Vénus et les ouragans sont caractérisés par différentes échelles horizontales et durée de vie: le vortex de Vénus à un diamètre de 12000 km et il semble être permanent; les plus grands cyclones tropicaux observés sur la Terre ont un rayon de moins de 1000 km et durent environ une à deux semaines dans leur phase de maturité. La source d'énergie est aussi différente pour le vortex sur Vénus et les ouragans terrestres: la source d'énergie pour les ouragans est la libération de chaleur latente; le vortex polaire sur Vénus reçoit un apport d'énergie par le dépôt du rayonnement solaire au niveau des nuages et par l'émission thermique dans la basse atmosphère. Malgré leurs différences, les circulations du vortex de Vénus et des ouragans est très similaires: à partir du leur comparaison une meilleure compréhension de la dynamique de Vénus peut être atteinte.
Figure 2

(Gauche) Le vortex polaire de Vénus; (Droit) l'ouragan Frances sur la Terre.
Crédit :
Limaye et al., 2009
 Tourbillons de poussière sur la Terre et Mars
Tourbillons de poussière sur la Terre et Mars
Les tourbillons de poussière, présents à la fois sur la Terre et Mars, sont caractérisés par des vitesses de vent de rotation élevées, des champs électrostatiques importants et sont rendus visibles par la présence de poussière et de sable soulevé. Ils sont distincts des tornades car les tornades sont associées à des orages tandis que les tourbillons de poussière se forment sous un ciel clair.
Sur la Terre (Figure 3), l'étude de tourbillons de poussière est fondamentale pour comprendre leur rôle dans la convection et l'érosion des zones arides. Les tourbillons de poussière se produisent généralement en été dans les régions désertiques plus chaudes. Ils sont des événements transitoires et la plupart ne durent que quelques minutes.
Figure 3

Tourbillon de poussière sur la Terre observé dans le désert de l'Arizona.
Crédit :
NASA
Sur Mars (Figure 4), les tourbillons de poussière peuvent avoir un effet important sur le cycle global de poussière. Les tourbillons de poussière sur Mars ont d'abord été identifiés dans les images prises par l'orbiteur Viking comme des petits nuages avec des longues ombres coniques. En plus, des traces laissées au sol par des tourbillons de poussière ont été détectées dans des images de la Mars Orbiter Camera et ont été également observées au sol par des atterrisseurs. Les tourbillons de poussière martiens et terrestres semblent avoir une morphologie similaire. Cependant, les tourbillons de poussière martiens sont un ordre de grandeur plus grand que ceux terrestres, atteignant souvent quelques kilomètres d'altitude et des centaines de mètres de diamètre avec des bases étroites et des larges sommets.
Figure 4

Tourbillon de poussière sur Mars photographié par le rover Spirit.
Crédit :
NASA
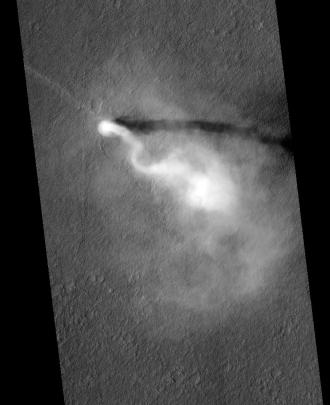
Tourbillon de poussière de 140 m de diamètre et 20 km de hauteur vu depuis l'orbite par l'intrument HiRISE.
Crédit :
NASA / JPL / University of Arizona / HiRISE
Instabilités
Auteurs: Thomas Navarro, Arianna Piccialli
Nombre de Richardson
 Interprétation
Interprétation
Ondes atmosphériques
Auteurs: Thomas Navarro, Arianna Piccialli
Caractéristiques des ondes
Les ondes atmosphériques sont des perturbations des champs atmosphériques qui se propagent dans l'espace et/ou le temps. C'est un mécanisme important dans la dynamique des atmosphères car les ondes permettent de transporter des perturbations, transporter de l'énergie et de la quantité de mouvement d'une région à une autre.
Onde sonore
Onde sonore
L'onde la plus évidente est l'onde sonore dont le calcul va être détaillé ci-dessous. On définit les petites perturbations comme étant des ondes se propageant horizontalement et verticalement :
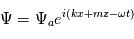
avec 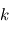 et
et 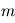 les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les équations primitives la force de Coriolis s'annule, tout comme la force centrifuge. En posant
les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les équations primitives la force de Coriolis s'annule, tout comme la force centrifuge. En posant 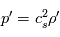 avec
avec 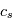 la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
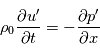
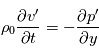
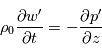
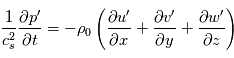
Soit, en utilisant les propriétés de la notation exponentielle :
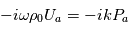
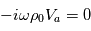
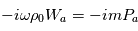
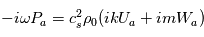
Par identification, on obtient :
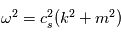
qui nous donne la relation entre longueur d'onde et période d'une onde sonore.
Généralisation
Le traitement des ondes atmosphériques est un sujet complexe; dans la page qui suit, nous allons donner un aperçu général des principaux types d'ondes en comparant différentes planètes, mais sans entrer dans le détail.
Une analyse plus détaillée des phénomènes ondulatoires peut être trouvé dans la liste suivante des livres:
- A. Sanchez-Lavega "An Introduction to Planetary atmospheres" CRC Press, Taylor & Francis Group, 2011.
- J. Holton "An Introduction to Dynamic Meteorology" Elsevier Academic Press, 2004.
Exemples d'ondes atmosphériques
Les ondes atmosphériques peuvent se manifester de diverses manières: comme oscillations de la température, de la densité et de la vitesse du vent, ou à travers des structures régulières de nuages. Ils peuvent être classés sur la base de facteurs différents: (1) mécanismes de restauration; (2) échelles de temps et d'espace; (3) ondes stationnaires ou qui se déplacent.
 Classement des ondes
Classement des ondes
- Ondes de gravité:
Le mécanisme de restauration des ondes de gravité est la poussée d'Archimède. Elles sont créées: (1) par la topographie (ondes orographiques), lors du passage d'une masse d'air au-dessus d'un relief montagneux; ou (2) par des instabilités dues à la présence d'orages ou de fronts d'air. Ils sont très communs dans les mésosphères des planètes telluriques. Sur Terre, les ondes de gravité révèlent souvent leur présence à travers des formations nuageuses, comme dans le cas des ondes orographiques. À des altitudes plus élevées, des images des nuages polaires mésosphériques, aussi connus sous le nom de nuages noctulescents, montrent souvent des structures ondulatoires probablement dues à la propagation vers le haut des ondes de gravité. Dans l'atmosphère martienne, des ondes de gravité ont été observées dans des images de nuages mésosphériques de glace de CO2 obtenues par la High Resolution Stereo Camera à bord de la mission européenne Mars Express et elles sont produites par la topographie (montagnes et cratères). Plusieurs missions spatiales ont détecté des ondes de gravité dans l'atmosphère de Vénus à la fois comme des oscillations sur le champ de température et comme des structures sur la couche de nuages. Elles sont probablement causées par des mouvements convectifs ou par des instabilité de de Kelvin-Helmholtz. Dans la haute atmosphère des planètes géantes (Jupiter, Uranus, et Neptune), des ondes de gravité ont été détectées par des oscillations dans les profils verticaux de température. Elles sont probablement la manifestation d'ondes de gravité générées près de la tropopause se propageant vers le haut.
- Ondes de Kelvin-Helmholtz:
Ces ondes sont un type d'ondes de gravité produites par l'instabilité de Kelvin-Helmholtz (Figure 2).
- Ondes de Rossby:
Les ondes de Rossby ou ondes planétaires sont caracterisées par une grande longueur d'onde. Elles sont dues à la variation de la force de Coriolis selon la latitude, quand une masse d'air se déplace à latitudes plus ou moins élevées. Sur la Terre, les ondes de Rossby sont des phénomènes permanents dans les latitudes moyennes et sous-polaires. Souvent, des cyclones et des anticyclones se forment dans les crêtes de l'onde. De la même façon, des ondes de Rossby se forment dans l'atmosphère vers les régions polaires de Mars. Dans les planètes géantes Jupiter et Saturne, il y a une grande variété d'ondes atmosphériques à l'extérieur de la région équatoriale qu'on suppose être des ondes de Rossby. Sur Saturne, un système ondulatoire hexagonal existe autour du pôle Nord, qui pourrait être une onde de Rossby. On peut voir divers exemples d'ondes de Rossby sur différentes planètes dans la figure ci-contre.
- Ondes de marées thermiques:
Les ondes de marées thermiques sont des ondes d'échelle planétaire excitées par les variations de l'insolation du sol dues au cycle jour-nuit. Ces ondes se manifestent sur le champ de pression et sur les composants du vent et elles évoluent avec le temps solaire local. Les ondes de marée thermique dans l'atmosphère de Mars ont une amplitude beaucoup plus élevée que sur la Terre car le forçage thermique sur Mars est très fort à cause de l'absorption dans le proche infra-rouge du 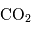 atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et méridienne moyenne est donc très important dans l'atmosphère martienne. Sur Vénus, l'absorption du rayonnement solaire se produit essentiellement dans la couche de nuages et des études ont proposé que les marées solaires jouent un rôle important dans la super-rotation de Vénus à ce niveau.
atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et méridienne moyenne est donc très important dans l'atmosphère martienne. Sur Vénus, l'absorption du rayonnement solaire se produit essentiellement dans la couche de nuages et des études ont proposé que les marées solaires jouent un rôle important dans la super-rotation de Vénus à ce niveau.
Figure 1

Crédit :
A. Piccialli
Figure 2

Ondes de Kelvin-Helmholtz observés au-dessus de Rome.
Crédit :
Angelo Zinzi
Réponses aux exercices
pages_planetologie-dynamique/coord-sphere.html
Exercice
pages_planetologie-dynamique/equations-dynamique.html
Exercice
pages_planetologie-dynamique/equations-dynamique.html
Exercice
pages_planetologie-dynamique/equilibres-dynamiques.html
Exercice
- Question 1
Aide :
- Utiliser la loi des gaz parfaits
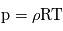
- La définition de géopotentiel :
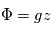 , avec
, avec 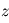 la hauteur et
la hauteur et 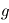 l'accélération gravitationnelle
l'accélération gravitationnelle - L'approximation hydrostatique :
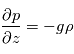
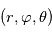 , où
, où 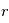 est la distance au centre de la sphère,
est la distance au centre de la sphère, 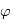 est la l'angle de la longitude, et
est la l'angle de la longitude, et 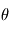 est l'angle de la latitude.
est l'angle de la latitude.
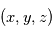 , avec comme base le triplet
, avec comme base le triplet 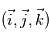 où
où 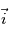 est dirigé vers l'Est,
est dirigé vers l'Est, 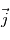 dirigé vers le Nord, et
dirigé vers le Nord, et 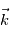 selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
selon la verticale locale vers le haut. Le référentiel d'étude est ce référentiel local, lié à la rotation de la planète, il s'agit donc d'un référentiel tournant, donc non galiléen.
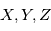 ).
).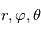 ).
).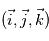 , qui est un système de coordonnées cartésiennes.
, qui est un système de coordonnées cartésiennes. Exercice
Exercice a pour coordonnées cartésiennes
a pour coordonnées cartésiennes 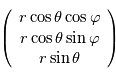
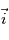 ,
, 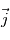 et
et 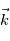 dans le repère de la planète en fonction des angles
dans le repère de la planète en fonction des angles 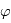 et
et 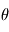
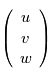 au point de coordonnées sphériques
au point de coordonnées sphériques  s'exprime par
s'exprime par 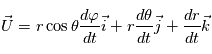 .
.
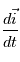 ,
, 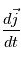 et
et 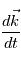 en fonction de
en fonction de 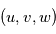 ,
, 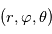 et
et 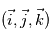 .
.

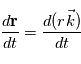 en gardant en tête que
en gardant en tête que 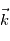 est un vecteur local qui dépend de la position, donc varie avec les coordonnées
est un vecteur local qui dépend de la position, donc varie avec les coordonnées 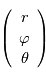 .
.
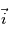 ,
, 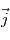 et
et 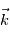 en fonction des angles
en fonction des angles 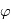 et
et 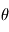 .
.
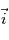 ,
, 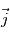 ,
, 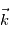 ,
, 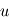 ,
, 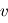 et
et 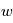 .
.
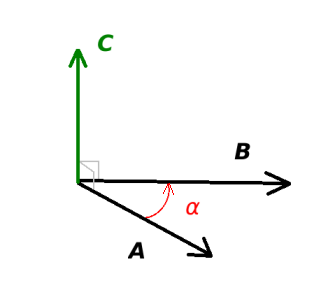
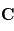 des vecteurs
des vecteurs 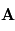 et
et 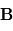 s'écrit
s'écrit 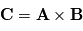 et correspond au vecteur orthogonal à la fois à
et correspond au vecteur orthogonal à la fois à 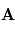 et
et 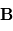 tel que le triplet
tel que le triplet 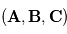 soit de sens direct. et que le module du produit soit
soit de sens direct. et que le module du produit soit 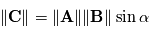 où
où 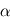 est l'angle direct de
est l'angle direct de 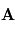 vers
vers 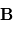 . Ainsi, si
. Ainsi, si 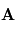 et
et 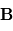 sont colinéaires, leur produit vectoriel sera le vecteur nul.
sont colinéaires, leur produit vectoriel sera le vecteur nul.
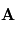 ,
, 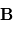 et
et 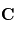 forment une base directe puisque
forment une base directe puisque 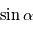 est positif. Si
est positif. Si 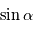 était négatif, la base serait dans le sens indirect.
était négatif, la base serait dans le sens indirect.
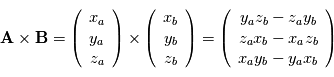
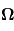 comme étant le vecteur orienté selon l'axe de rotation de la planète et de module
comme étant le vecteur orienté selon l'axe de rotation de la planète et de module 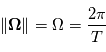 avec
avec 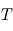 la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime
la période de rotation de la planète.
L'accélération de la force centrifuge s'exprime 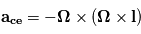 avec
avec 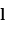 le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a
le vecteur position depuis l'axe de rotation où la force s'applique.
Dans un système de coordonnées sphériques, on a 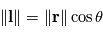 , avec
, avec 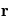 le vecteur position depuis le centre de la planète.
le vecteur position depuis le centre de la planète.
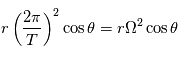
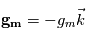 , l'indice
, l'indice 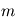 faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est
faisant référence à la masse de la planète. On obtient une force dont l'accélération totale est 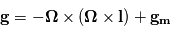 . Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
. Cette force dérive d'un potentiel, qu'on appelle le géopotentiel, somme de l'action de la gravité et de la force centrifuge.
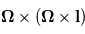 correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur
correspond bien à une accélération perpendiculaire à l'axe de rotation, orientée vers l'extérieur et de valeur 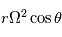 . Comment s'exprime cette accélération dans le référentiel local ?
. Comment s'exprime cette accélération dans le référentiel local ?
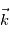 . Quelle erreur est faite pour la Terre ? pour Jupiter ?
. Quelle erreur est faite pour la Terre ? pour Jupiter ?
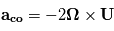 avec
avec 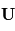 le vecteur vitesse de la parcelle d'air considérée.
le vecteur vitesse de la parcelle d'air considérée.
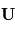 d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en général petite par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
d'une parcelle d'air dans l'atmosphère est généralement orientée parallèlement à la surface locale, c'est-à-dire que sa composante radiale (c'est-à-dire sa composante verticale locale) est en général petite par rapport à au moins une des deux autres. En négligeant la composante radiale, on constate les choses suivantes :
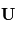
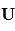
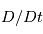 . Soit
. Soit ![\textbf{A}[\textbf{r}(t)]](../pages_planetologie-dynamique/equations_outils/equation165.png) une grandeur physique vectorielle de l'écoulement, dépendant du point d'observation
une grandeur physique vectorielle de l'écoulement, dépendant du point d'observation 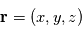 et du temps
et du temps 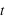 . La variation de la grandeur
. La variation de la grandeur 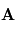 s'écrit :
s'écrit :
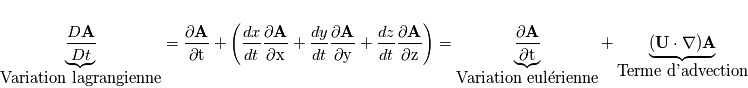
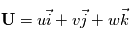 est la vitesse du fluide avec composants:
est la vitesse du fluide avec composants: 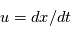 ,
, 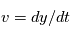 ,
, 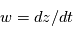 .
.
![f[\textbf{r}(t)]](../pages_planetologie-dynamique/equations_outils/equation174.png) , la relation est la même.
, la relation est la même.
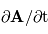 décrit la variation locale avec le temps en un point d'observation fixé (point de vue eulérien) .
décrit la variation locale avec le temps en un point d'observation fixé (point de vue eulérien) .
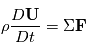 avec
avec 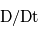 est la
est la 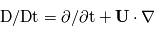 ,
, 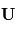 la vitesse du fluide,
la vitesse du fluide, 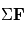 la somme des forces s'appliquant sur la parcelle et
la somme des forces s'appliquant sur la parcelle et 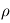 la densité du fluide.
la densité du fluide.
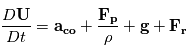
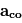 l'accélération de la
l'accélération de la 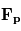 les forces dues au gradient de pression,
les forces dues au gradient de pression, 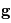 l'accélération du
l'accélération du 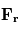 qui désigne l'accélération dues à la viscosité. Ce qui donne :
qui désigne l'accélération dues à la viscosité. Ce qui donne :
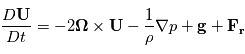 (1)
(1)
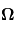 est le vecteur de rotation de la planète
est le vecteur de rotation de la planète 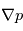 est le gradient de pression.
est le gradient de pression.
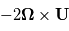 dans le repère local ?
dans le repère local ?
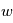 .
.
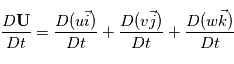 . Or
. Or 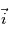 ,
,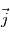 et
et 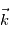 . Ceci nous permet d'établir les équations de Navier-Stokes dans le référentiel local, en notant que
. Ceci nous permet d'établir les équations de Navier-Stokes dans le référentiel local, en notant que 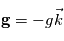 et
et 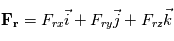 :
:

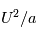
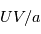
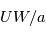
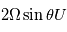
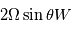
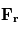
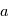 le rayon de la planète. On a
le rayon de la planète. On a 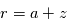 , où
, où 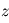 est l'altitude depuis la surface.
est l'altitude depuis la surface.
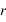 au centre de la planète par le rayon de la planète
au centre de la planète par le rayon de la planète 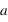 avec une erreur négligeable. Dans ce cas, les dérivées
avec une erreur négligeable. Dans ce cas, les dérivées 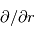 deviennent
deviennent 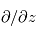 où
où 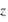 est l'altitude.
est l'altitude.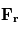 ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol.
ont un ordre de grandeur de 10-12 m s-2 et peuvent être négligées pour tous les écoulements, sauf pour les mouvements turbulents à petite échelle près du sol. 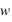 .
.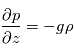
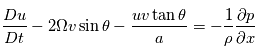
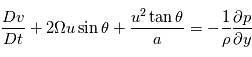
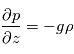
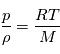
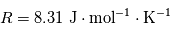 la constante universelle des gaz parfaits et
la constante universelle des gaz parfaits et 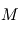 la masse molaire du gaz qui constitue l'atmosphère, et dépend donc de sa composition. Pour l'air terrestre, on a
la masse molaire du gaz qui constitue l'atmosphère, et dépend donc de sa composition. Pour l'air terrestre, on a 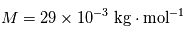
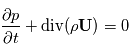
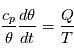
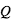 le forçage diabatique et
le forçage diabatique et 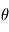 la température potentielle :
la température potentielle : ![\theta=T\left[\frac{p_0}{p}\right]^{\kappa}](../pages_planetologie-dynamique/equations_circulation-generale/equation229.png) , où
, où 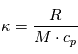 ,
, 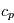 la chaleur spécifique à pression constante et
la chaleur spécifique à pression constante et 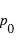 une pression de référence.
une pression de référence.
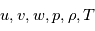 ).
).
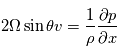
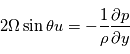

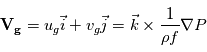
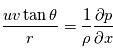
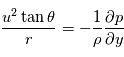
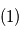

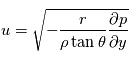
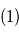 que l'équation du vent cyclostrophique peut être écrite comme :
que l'équation du vent cyclostrophique peut être écrite comme :
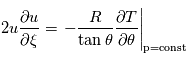
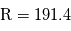 J kg-1 K-1, et
J kg-1 K-1, et 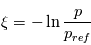 est la coordonnée de pression logarithmique, avec
est la coordonnée de pression logarithmique, avec 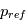 la pression au niveau de référence.
la pression au niveau de référence.
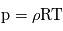
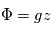 , avec
, avec 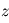 la hauteur et
la hauteur et 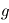 l'accélération gravitationnelle
l'accélération gravitationnelle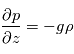
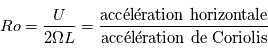
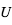 est une vitesse caractéristique du système,
est une vitesse caractéristique du système, 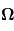 est la vitesse angulaire de rotation de la planète, et
est la vitesse angulaire de rotation de la planète, et 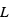 est une longueur caractéristique du système.
est une longueur caractéristique du système.
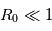
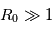
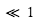
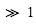
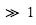
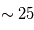 km jusqu'à
km jusqu'à 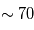 km, où ils atteignent une vitesse de 60 m s-1.
km, où ils atteignent une vitesse de 60 m s-1.
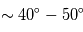 de latitude atteignant une vitesse maximale de 40 m s-1 à 5 km. Il augmente encore à 35 km, où il atteint une vitesse de 110 m s-1. A cette même époque, le courant-jet dans l'hémisphère sud est beaucoup plus faible.
de latitude atteignant une vitesse maximale de 40 m s-1 à 5 km. Il augmente encore à 35 km, où il atteint une vitesse de 110 m s-1. A cette même époque, le courant-jet dans l'hémisphère sud est beaucoup plus faible.
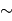 60 fois plus rapide que Vénus elle-même).
Différentes études ont montré que sur les planètes qui tournent lentement, comme Vénus et Titan, les forts vents zonaux au sommet des nuages peuvent être décrits par l’équilibre cyclostrophique. Ce qui donne une possibilité de reconstruire le vent zonal si le champ de température est connu.
60 fois plus rapide que Vénus elle-même).
Différentes études ont montré que sur les planètes qui tournent lentement, comme Vénus et Titan, les forts vents zonaux au sommet des nuages peuvent être décrits par l’équilibre cyclostrophique. Ce qui donne une possibilité de reconstruire le vent zonal si le champ de température est connu.

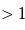 et peut arriver jusqu'à 100. Dans ce cas, l'équilibre devient cyclostrophique.
et peut arriver jusqu'à 100. Dans ce cas, l'équilibre devient cyclostrophique.




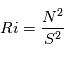
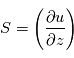 est le cisaillement vertical du vent.
est le cisaillement vertical du vent.
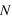 est nommée fréquence de Brunt-Väisälä définie comme la différence entre le gradient vertical de température
est nommée fréquence de Brunt-Väisälä définie comme la différence entre le gradient vertical de température 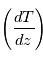 et le
et le 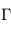 :
:
![N^2=\frac{g}{T}\left[\left(\frac{dT}{dz}\right)-\Gamma\right]](../pages_planetologie-dynamique/equations_instabilite/equation6.png)
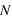 est la fréquence d'oscillation d'une particule soumise à un déplacement vertical. Pour
est la fréquence d'oscillation d'une particule soumise à un déplacement vertical. Pour 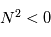 l'atmosphère est instable et une particule déplacée de son état initial s'éloignera irréversiblement. Si
l'atmosphère est instable et une particule déplacée de son état initial s'éloignera irréversiblement. Si 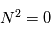 , la stabilité est "neutre", la particule déplacée demeura à sa nouvelle altitude. Enfin, pour
, la stabilité est "neutre", la particule déplacée demeura à sa nouvelle altitude. Enfin, pour 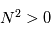 se produit une oscillation de la particule autour de son état initial.
se produit une oscillation de la particule autour de son état initial.
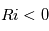 : Instabilité verticale
: Instabilité verticale
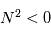 , la couche atmosphérique est instable et la turbulence est soutenue par la
, la couche atmosphérique est instable et la turbulence est soutenue par la 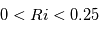 : Instabilité de Kelvin-Helmholtz
: Instabilité de Kelvin-Helmholtz
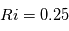 est une condition nécessaire afin que l'instabilité de Kelvin-Helmholtz se puisse produire. L'écoulement de Kelvin-Helmholtz est le résultat du cisaillement de vitesse entre deux fluides glissant l'un par rapport à l'autre.
est une condition nécessaire afin que l'instabilité de Kelvin-Helmholtz se puisse produire. L'écoulement de Kelvin-Helmholtz est le résultat du cisaillement de vitesse entre deux fluides glissant l'un par rapport à l'autre.
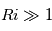 : Atmosphère stable
: Atmosphère stable
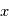 et d'une dimension temporelle de coordonnée
et d'une dimension temporelle de coordonnée 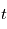 :
:
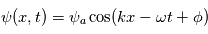
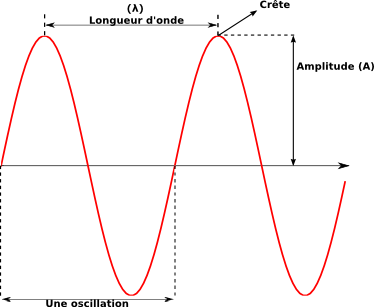
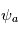 est l'amplitude de l'onde;
est l'amplitude de l'onde; 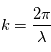 est le nombre d'onde;
est le nombre d'onde; 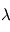 est la longueur d'onde (en mètres);
est la longueur d'onde (en mètres); 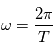 est la pulsation;
est la pulsation; 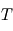 est la période (en secondes).
est la période (en secondes). 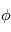 est la phase de l'onde, c'est-à-dire la valeur de la perturbation lorsque
est la phase de l'onde, c'est-à-dire la valeur de la perturbation lorsque 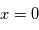 et
et 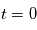 .
La longueur d'onde est définie comme étant la distance séparant deux crêtes consécutives d'une onde. Si
.
La longueur d'onde est définie comme étant la distance séparant deux crêtes consécutives d'une onde. Si 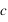 (en mètres par seconde) est la vitesse de propagation de l'onde, on définit la fréquence (en hertz) par :
(en mètres par seconde) est la vitesse de propagation de l'onde, on définit la fréquence (en hertz) par : 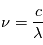 .
.
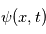 est une variable atmosphérique. Il peut s'agir de la température, pression, le vent, etc ... La dimension de l'amplitude
est une variable atmosphérique. Il peut s'agir de la température, pression, le vent, etc ... La dimension de l'amplitude 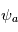 est donc la même que celle de la variable représentée par la perturbation
est donc la même que celle de la variable représentée par la perturbation  .
.
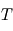 , l'onde aura aura la même allure.
, l'onde aura aura la même allure.
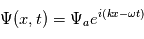
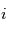 le nombre imaginaire
le nombre imaginaire 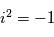 . La perturbation réelle est définie comme étant la partie réelle de sa forme complexe :
. La perturbation réelle est définie comme étant la partie réelle de sa forme complexe :
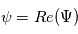
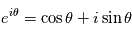 , on obtient que l'amplitude complexe
, on obtient que l'amplitude complexe 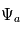 vaut :
vaut :
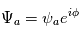
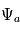 contient ainsi l'information à la fois sur l'amplitude
contient ainsi l'information à la fois sur l'amplitude 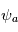 et la phase
et la phase 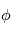 de l'onde. Cette notation est très pratique car elle permet notamment de dériver ou d'intégrer une onde par rapport à l'espace ou au temps. Par exemple :
de l'onde. Cette notation est très pratique car elle permet notamment de dériver ou d'intégrer une onde par rapport à l'espace ou au temps. Par exemple :
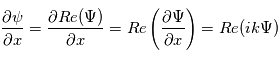
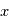 revient à multiplier l'onde complexe par
revient à multiplier l'onde complexe par 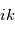 . De même, une dérivation temporelle revient à multiplier par
. De même, une dérivation temporelle revient à multiplier par 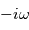 .
.
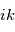 , donc à multiplier par
, donc à multiplier par 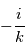 . De même, multiplier par
. De même, multiplier par 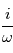 permet de trouver une primitive par rapport à
permet de trouver une primitive par rapport à 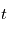 .
.
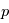 ) comme étant la somme d'une valeur fixe
) comme étant la somme d'une valeur fixe 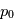 solution des équations et d'une petite perturbation
solution des équations et d'une petite perturbation 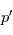 :
: 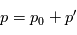 . Ceci permet de linéariser les équations primitives en obtenant une équation pour les petites pertubations. Ces pertubations correspondent à des ondes que l'on peut ainsi étudier au moyen d'un cadre formel.
. Ceci permet de linéariser les équations primitives en obtenant une équation pour les petites pertubations. Ces pertubations correspondent à des ondes que l'on peut ainsi étudier au moyen d'un cadre formel.
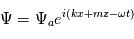
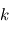 et
et 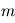 les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les
les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les 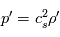 avec
avec 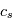 la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
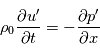
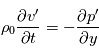
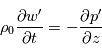
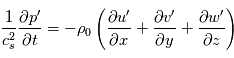
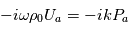
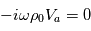
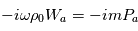
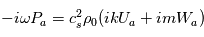
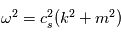
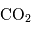 atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et
atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et 
