
La barrière du mètre |
Comme nous l’avons vu (cf. lien), une des étapes les plus délicates du scénario standard de formation planétaire est celle qui fait passer des premières poussières condensées dans la nébuleuse aux planétésimaux kilométriques. La principale difficulté étant atteinte pour des corps de ∼10cm-1m, pour lesquels les vitesses de collision deviennent trop élevées pour permettre l’accrétion, et qui vont de plus avoir un mouvement de dérive très rapide vers l’étoile centrale. Ces deux problèmes sont tous deux liés à l’action du gaz sur les corps solides. En effet, toute particule solide plongée dans un milieu gazeux subit la friction de ce gaz, qui va être proportionnelle à la surface de contact entre le gaz et l’objet. Cette friction peut ainsi s’exprimer sous la forme
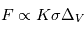
Où 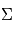 est la section efficace du corps (
est la section efficace du corps (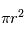 ) et
) et 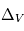 la différence de vitesse entre le gaz et la particule.
Si maintenant on applique le principe fondamental de la dynamique, on obtient que l’accélération
la différence de vitesse entre le gaz et la particule.
Si maintenant on applique le principe fondamental de la dynamique, on obtient que l’accélération 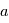 due au gaz vaut:
due au gaz vaut:
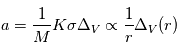
On pourrait a priori se dire que, dans le cas présent, 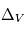 est nul car aussi bien le gaz que les corps solides orbitent autour de l’étoile suivant les mêmes lois de Kepler, et donc en principe à la même vitesse orbitale
est nul car aussi bien le gaz que les corps solides orbitent autour de l’étoile suivant les mêmes lois de Kepler, et donc en principe à la même vitesse orbitale 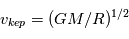 . Mais il y a en fait une différence, car le gaz est lui, en plus, soumis à une force de pression due au gradient de température et de densité dans la nébuleuse. Dans un disque proto-planétaire de type MMSN, cette force de pression s’exerce de l’intérieur vers l’extérieur et tend donc à contrebalancer la gravitation de l’étoile. Tout se passe donc comme si le gaz « percevait » une étoile de masse
. Mais il y a en fait une différence, car le gaz est lui, en plus, soumis à une force de pression due au gradient de température et de densité dans la nébuleuse. Dans un disque proto-planétaire de type MMSN, cette force de pression s’exerce de l’intérieur vers l’extérieur et tend donc à contrebalancer la gravitation de l’étoile. Tout se passe donc comme si le gaz « percevait » une étoile de masse 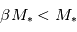 et aura donc une vitesse Képlérienne
et aura donc une vitesse Képlérienne 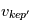 inférieure au
inférieure au 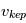 d’un corps solide orbitant dans la vide. On dit alors que le disque de gaz est « sub-Képlérien ».
d’un corps solide orbitant dans la vide. On dit alors que le disque de gaz est « sub-Képlérien ».
Le comportement de corps solides plongés dans ce disque de gaz est alors compris entre 2 extrêmes : les particules les plus petites (<mm) sont piégées dans le gaz et bougent avec lui, et on a dans ce cas 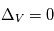 et donc
et donc 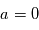 . A l’autre extrême, les planétésimaux très massifs sont, eux, découplés du gaz et subissent de la friction, mais ne vont pas beaucoup en pâtir car le rapport
. A l’autre extrême, les planétésimaux très massifs sont, eux, découplés du gaz et subissent de la friction, mais ne vont pas beaucoup en pâtir car le rapport  est tout petit et ils vont donc être très difficile à bouger par le gaz. Donc la aussi
est tout petit et ils vont donc être très difficile à bouger par le gaz. Donc la aussi 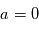 . Entre ces 2 extrêmes, il existe un régime intermédiaire avec des corps suffisamment gros pour être découplés du gaz (
. Entre ces 2 extrêmes, il existe un régime intermédiaire avec des corps suffisamment gros pour être découplés du gaz ( 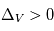 ) mais pas suffisamment massifs pour être insensibles à la friction. Ce régime de taille intermédiaire se situe autour de 10cm-1m. Pour des corps de cette taille l’effet de la friction gazeuse est maximal (cf. image). Et comme
) mais pas suffisamment massifs pour être insensibles à la friction. Ce régime de taille intermédiaire se situe autour de 10cm-1m. Pour des corps de cette taille l’effet de la friction gazeuse est maximal (cf. image). Et comme 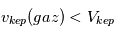 , cette friction aura tendance à ralentir les corps solides et à les faire dériver vers l’étoile. Cette vitesse de dérive peut atteindre plus de 50m/s, ce qui correspond à 1UA en moins de 100ans !
, cette friction aura tendance à ralentir les corps solides et à les faire dériver vers l’étoile. Cette vitesse de dérive peut atteindre plus de 50m/s, ce qui correspond à 1UA en moins de 100ans !