Effet de serre

Auteur: EM

Cadre du modèle

Dans un modèle purement radiatif d'une colonne d'atmosphère (sans convection ni conduction), il est relativement facile d'estimer l'effet de serre causé par une atmosphère (transparente en lumière visible et partiellement opaque au rayonnement infrarouge thermique) entourant une planète tellurique.

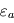On supposera que la surface possède une émissivité égale à en infrarouge thermique, et que celle de l'atmosphère (directement reliée à son absorbance via la loi de Kirchhoff) est prise constante et égale à $\varepsilon_a$ dans tout le domaine infrarouge thermique (c'est ce que l'on appelle l'approximation grise). L'atmosphère est considérée ici isotherme à la température 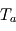T_a . On négligera aussi les flux d'énergie éventuels provenant de l'intérieur de la planète, et on supposera que l'étoile émet de façon négligeable dans l'infrarouge thermique, situé loin de son maximum d'émission dans le visible (ou le proche IR pour les plus froides d'entre elles).

Bilans de flux

Représentation des flux rayonnants

Représentation schématique des flux (bleu pour le domaine stellaire visible-UV-proche IR, rouge pour le domaine infrarouge thermique).

Crédit : Emmanuel Marcq

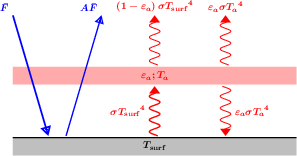
La situation est très simple pour les flux stellaires. 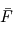$\bar{F}$ désigne le flux moyen à la surface de la planète, qui se déduit du flux à incidence normale appelé constante solaire (ou stellaire) par l'égalité des puissances : 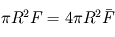$\pi R^2 F = 4 \pi R^2 \bar{F}$ (voir le raisonnement définissant la température d'équilibre pour plus de détails, 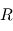désigne ici le rayon planétaire). On en déduit immédiatement 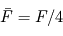$\bar{F} = F/4$ : un facteur 2 s'explique aisément par le fait que seul un hémisphère est éclairé, et l'autre facteur 2 par la moyenne du cosinus de l'angle d'incidence intervenant dans le calcul local du flux.

En vertu de la définition de l'émissivité, l'atmosphère rayonne donc 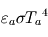$\varepsilon_a \sigma {T_a}^4$ dans chacun des demi-espaces inférieur (vers la surface) et supérieur (vers l'espace). En vertu de la loi de Kirchhoff, cette émissivité est égale à son absorbance, si bien que la fraction complémentaire 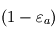$\left( 1 - \varepsilon_a \right)$ du rayonnement en provenance de la surface (considérée comme un corps noir) réussit à la traverser, le reste étant absorbé (on néglige les processus de diffusion ici ; seules les émissions et absorptions sont prises en compte).

Le bilan des flux à la surface donne alors à l'équilibre radiatif (synonyme d'égalité entre la somme des flux entrants et la somme des flux sortants) : 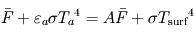$\bar{F} + \varepsilon_a \sigma {T_a}^4 = A \bar{F} + \sigma {T_{\mathrm{surf}}}^4$ , tandis que celui au niveau de la couche atmosphérique donne 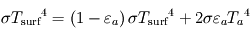$\sigma {T_{\mathrm{surf}}}^4 = \left(1 - \varepsilon_a \right) \sigma {T_{\mathrm{surf}}}^4 + 2 \sigma \varepsilon_a {T_a}^4$ . 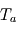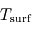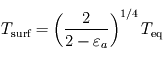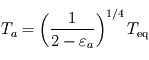Nous avons donc deux équations pour les deux inconnues T_a et $T_{\mathrm{surf}}$ , et la résolution du système donne alors : $T_{\mathrm{surf}} = \left( \frac{2}{2 - \varepsilon_a} \right)^{1/4} T_{\mathrm{eq}}$ et $T_a = \left( \frac{1}{2 - \varepsilon_a} \right)^{1/4} T_{\mathrm{eq}}$ où l'on aura reconnu la température d'équilibre $T_{\mathrm{eq}} = \left[\frac{(1-A) F}{4 \sigma} \right]^{1/4} = \left[\frac{(1-A) \bar{F}}{\sigma} \right]^{1/4}$ définie précédemment.

Discussion

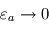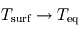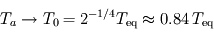Dans la limite transparente où $\varepsilon_a \to 0$ , $T_{\mathrm{surf}} \to T_{\mathrm{eq}}$ et $T_a \to T_0 = 2^{-1/4} T_{\mathrm{eq}} \approx 0.84 \, T_{\mathrm{eq}}$ : la surface retrouve alors la température d'équilibre, ce qui est normal pour une atmosphère à la fois transparente en lumière stellaire et en infrarouge thermique (atmosphère radiativement inerte ne causant aucun effet de serre). La température atmosphérique tend alors vers une valeur 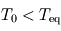$T_0 < T_{\mathrm{eq}}$ appelée température de peau et typique des couches quasi-transparentes en approximation grise.
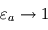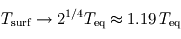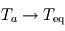Dans la limite opaque où $\varepsilon_a \to 1$ , $T_{\mathrm{surf}} \to 2^{1/4} T_{\mathrm{eq}} \approx 1.19\,T_{\mathrm{eq}}$ et $T_a \to T_{\mathrm{eq}}$ : le rayonnement s'échappant vers l'espace provient alors uniquement de l'atmosphère, qui se met donc à la température d'équilibre. La surface reçoit donc du rayonnement infrarouge atmosphérique en plus du seul rayonnement stellaire (qui pris isolément la maintiendrait déjà à une température de 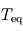$T_{\mathrm{eq}}$ ), si bien que sa température s'élève : c'est ce que l'on appelle l'effet de serre, plafonnant dans ce modèle à une seule couche atmosphérique isotherme à une augmentation de la température absolue (mesurée en Kelvins) de $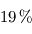19\,\%$ .