Pulsation de coupure
Difficulté : ☆☆
Temps : 30 min
On échantillonne un signal temporel avec un pas de temps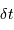 
. On définit la pulsation 
.
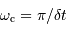Question 1)
Montrer qu'il y a confusion entre les spectres de puissance des signaux périodiques de pulsation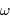 
et
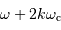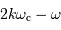ou 
, où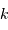 
est un entier
AideAideAideSolution
Courage, ce n'est qu'un peu de calculs sur les sinus.
Estimer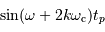 
à une date 
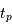de l'échantillonnage
Supposer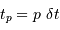 
On suppose, sans restreindre la généralité, que le signal est de forme sinusoïdale, et l'on choisit l'origine des temps de façon à avoir la p-ième date de l'échantillon vérifiant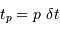 
.
On en déduit :
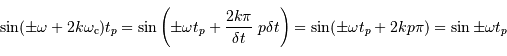
Au signe près, auquel n'est pas sensible le spectre de puissance (TF
),
cette égalité est assurée à toute date de l'échantillonnage.
Question 2)
En déduire l'expression de la pulsation de coupure
AideSolution
Jusqu'à quelle fréquence n'y aura-t-il pas de confusion?
La 1ère confusion va apparaître pour les pulsations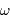 
telles que
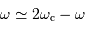, càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
S'exercer