
Image en rayon X du Soleil. Quelle source d'énergie interne explique la luminosité du Soleil ?
Crédit :
NASA
Energie interne
Le Soleil présente un âge bien plus avancé que le temps de Kelvin-Helmholtz. Il possède une source d'énergie interne qui explique son rayonnement.
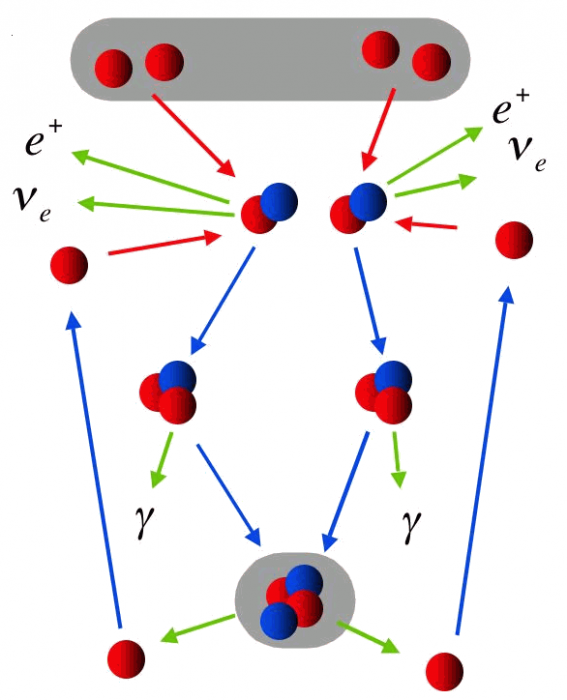
Réaction détaillée de la fusion de 4 H en 1 He.
Crédit :
ASM
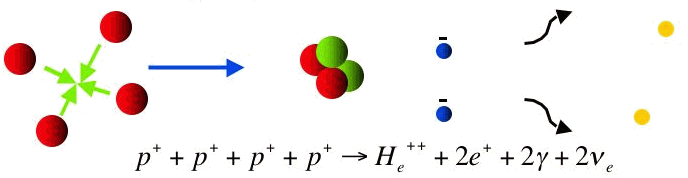
Bilan de la fusion de 4 H en 1 He.
Crédit :
ASM
Chaine proton-proton
Différentes étapes conduisent à la fusion de 4 protons en un noyau d'hélium, ne faisant intervenir que des paires de réactifs à chaque étape élémentaire.
L'étape limitante de la réaction consiste en la fusion de 2 protons vers un noyau de deutérium, avec émission d'un positron, donc un bilan réduit  . L'interaction faible mise en jeu induit un très faible taux de réaction.
. L'interaction faible mise en jeu induit un très faible taux de réaction.
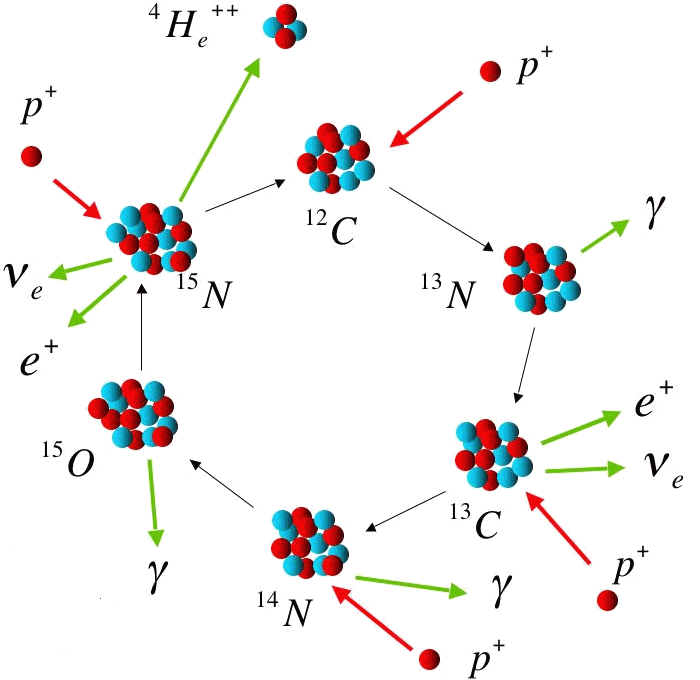
Cycle CNO.
Crédit :
ASM
Cycle CNO
A plus haute température (car les noyaux impliquées sont plus lourds, donc plus chargés), le cycle CNO peut s'avérer plus rapide que la chaîne proton-proton. Il est à l'oeuvre dans les étoiles massives. Les noyaux C, N et O participent au cycle, mais n'apparaissent pas dans le bilan final, qui reste la transformation de 4 protons en 1 noyau d'hélium.
 Objectifs
Objectifs
Définir dans quelles conditions microphysiques la fusion de l'hydrogène va s'amorcer.
Montrer que la fusion nécessite une température élevée, de l'ordre de 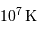 .
.

Seules les régions internes les plus chaudes peuvent être le siège de la fusion de l'hydrogène. Leur volume est limité.
Crédit :
ASM
Constante de temps nucléaire
La durée de vie à ce régime, pour une étoile comme le Soleil, est alors :
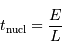
L'application numérique, avec la luminosité solaire mesurée aujourd'hui 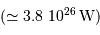 , le taux de conversion par nucléon et la masse concernée donne :
, le taux de conversion par nucléon et la masse concernée donne :
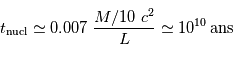
Une réaction chimique, dégageant typiquement 1 eV par nucléon, soit 1 million de fois moins que la fusion de l'hydrogène, conduirait à une durée de vie de 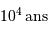 seulement.
seulement.
L'estimation de 10 milliards d'année pour le Soleil est très proche de ce que donne une modélisation plus poussée. Actuellement, avec un âge de 4.56 milliards d'années, le Soleil est à mi-parcours sur la
séquence principale.
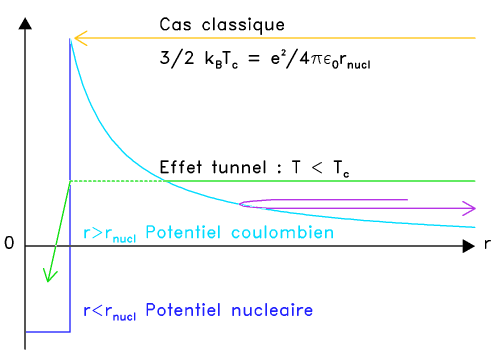
L'effet tunnel permet à un couple de protons de se rencontrer et d'interagir via l'interaction nucléaire forte, en outrepassant la barrière électrostatique.
Crédit :
ASM
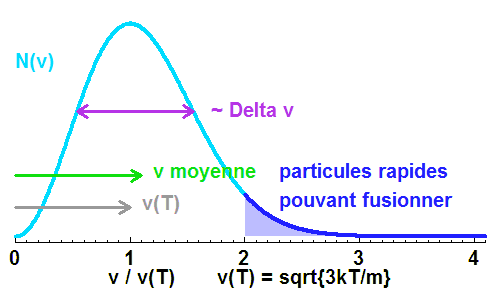
Distribution maxwellienne de vitesse, valable pour un gaz parfait. Valeur la plus probable, valeur moyenne et largeur de la distribution se valent, pour une énergie cinétique égale à 3/2 kT.
Crédit :
ASM
Interagir
Au sein d'une étoile, l'hydrogène est totalement ionisé : la matière se présente sous la forme d'un gaz de protons et d'électrons essentiellement. La réaction entre 2 protons nécessite leur rencontre à très courte distance, car l'interaction nucléaire forte n'a qu'une très courte portée, de l'ordre du femtomètre. Ceci nécessite de vaincre la répulsion électrostatique.
La barrière de potentiel pour une distance de 1 fm entre les 2 protons, peut se traduire en température : de l'ordre de 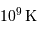 . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
. Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
Deux phénomènes se conjuguent pour faciliter la fusion :
- L'effet tunnel conduit à tromper les électrons sur la distance exacte qui les sépare. Il exprime l'incertitude de Heisenberg : les 2 protons fonçant l'un sur l'autre ne peuvent pas avoir une position très précisément définie.
- La distribution de vitesse des protons est maxwellienne, donnée par la théorie cinétique du gaz parfait : si l'énergie cinétique moyenne est
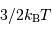 , une proportion non négligeable de protons est sensiblement plus rapide.
, une proportion non négligeable de protons est sensiblement plus rapide.
Ces points sont quantifiés en exercice.
Fusion de l'hydrogène
En pratique, la température limite de fusion de l'hydrogène est de l'ordre de 10 millions de Kelvin. Pour des températures plus faibles, seule la fusion du deutérium peut s'amorcer.
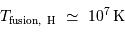
La fusion par le cycle pp domine lorsque la température n'excède pas 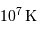 . Au delà de
. Au delà de 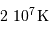 , le cycle CNO est prépondérant.
, le cycle CNO est prépondérant.
Fusion de noyaux lourds
Plus les noyaux sont lourds, plus leur fusion nécessite une température élevée. En fonction du nombre de charge  de l'élément considéré :
de l'élément considéré :
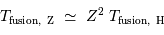
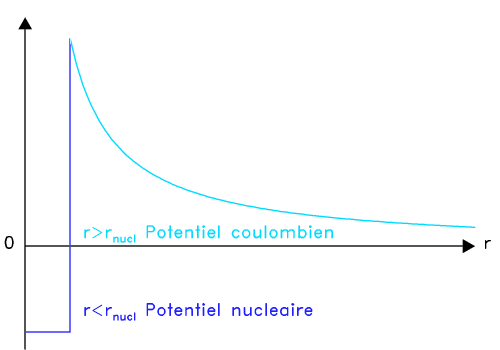
Energie potentielle d'interaction proton-proton.
Crédit :
ASM
 Température de fusion
Température de fusion
Difficulté : ☆☆
Temps : 40 min
Cet exercice a pour but de quantifier, dans un cadre classique, la température minimale qui doit régner au centre d'une étoile pour que s'amorcent les réactions nucléaires. Il se base sur la figure donnant le potentiel d'interaction entre 2 protons.
Question 1)
Mener un bilan d'énergie, pour déterminer l'énergie cinétique minimale conduisant à la fusion.
[1 points]
Exprimer l'énergie de la barrière coulombienne.
Exprimer la condition énergétique limite à remplir en 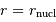
Question 2)
En déduire l'expression de la température minimale pour que la fusion puisse avoir lieu.
[2 points]
Faire le lien entre l'énergie cinétique et la température.
Question 3)
Faire l'application numérique. On donne 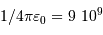 en unité SI, et
en unité SI, et 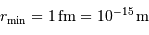 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
[2 points]
Question 4)
Comment s'écrit cette température s'il s'agit de faire fusionner non pas 2 protons, mais 2 noyaux d'une élément de charge 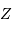 .
.
En déduire que la température de fusion des éléments lourds nécessite une température bien plus élevée que celle pour l'hydrogène.
[1 points]
Réécrire le potentiel électrostatique en fonction de 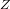 .
.
L'effet varie comme 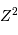
 Du rôle de l'effet tunnel et de la distribution des vitesses
Du rôle de l'effet tunnel et de la distribution des vitesses
Difficulté : ☆☆☆
Temps : 60 min
Sans effet tunnel, la
fusion de l'hydrogène nécessiterait des températures très élevées (et p.ex. non atteintes dans l'intérieur du Soleil). Cet exercice a pour but de décrire le rôle de l'effet tunnel dans le cadre d'un modèle très simplifié.
On note 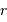 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 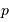 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
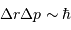
Question 1)
Relier la distance minimale d'approche des 2 protons à la quantité de mouvement incidente, puis à la température du milieu.
[1 points]
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
Question 2)
Faire l'application numérique dans le cas d'une distance d'approche de 1 fm, nécessaire pour arriver à une interaction forte entre les protons.
[1 points]
Question 3)
Dans le problème étudié, la loi de distribution des vitesses permet de confondre 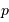 et
et 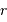 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
On suppose que le proton incident ne sait pas localiser l'autre proton, avec une incertitude dépendant de sa quantité de mouvement incidente précédemment calculée (notée simplement 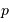 ).
).
Déterminer alors cette incertitude de position.
[3 points]
La relation d'incertitude présentée ici se traduit par
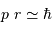
L'égalité entre l'énergie cinétique à grande distance 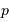 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 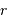 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
Question 4)
Faire l'application numérique (on donne 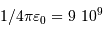 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
[2 points]
Question 5)
La distribution des quantités de mouvement assure qu'il existe une population avec des protons 3 fois plus rapide que la valeur moyenne. En déduire la température minimale pour la fusion.
[1 points]
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
- Question 1
Aide :
Exprimer l'énergie de la barrière coulombienne.
Aide :
Exprimer la condition énergétique limite à remplir en 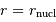
Solution :
L'énergie totale d'un proton s'écrit :
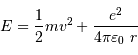
Pour passer la barrière coulombienne en 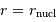 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
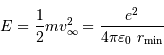
(énergie potentielle nulle à l'infini, énergie cinétique nulle au niveau de la barrière).
- Question 2
Aide :
Faire le lien entre l'énergie cinétique et la température.
Solution :
La température minimale vérifie :
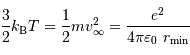
Soit :
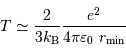
- Question 3
Solution :
Avec les valeurs proposées, on trouve :
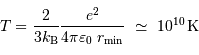
Cette valeur est surestimée, car ne prend pas en compte les phénomènes quantiques qui relaxent considérablement les conditions de fusion.
- Question 4
Aide :
Réécrire le potentiel électrostatique en fonction de 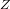 .
.
Aide :
L'effet varie comme 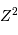
Solution :
Les équations précédentes se réécrivent avec la nouvelle énergie potentielle
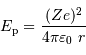
Il s'ensuit une température de fusion :
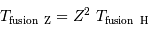
La valeur de la température est encore plus élevée que pour l'hydrogène.
- Question 1
Aide :
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
Aide :
Voir l'exercice
précédent
Solution :
L'exercice consacré à ce raisonnement donne la
solution. Avec les notations ici proposées :
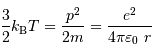
- Question 2
Aide :
Solution :
L'application numérique donne :
- Question 3
Aide :
La relation d'incertitude présentée ici se traduit par
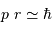
Aide :
L'égalité entre l'énergie cinétique à grande distance 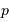 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 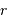 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
Solution :
En notant simplement 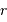 la distance minimale d'approche, et
la distance minimale d'approche, et 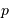 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
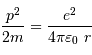
La relation d'incertitude présentée ici se traduit par
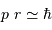 On en déduite la valeur de
On en déduite la valeur de 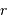 , en éliminant
, en éliminant 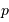 :
:
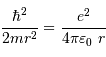
Et donc on aboutit à la nouvelle position (ou incertitude de position, d'après la présentation de l'énoncé) :
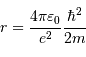
- Question 4
Solution :
L'application numérique donne :
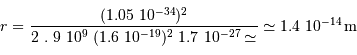
Cette distance est plus grande que 1 fm. Les protons peuvent donc se "tromper", et se croire en train de fusionner alors qu'ils sont 14 fois trop éloignés.
La température de fusion décroît de ce même facteur 14, soit de l'ordre de 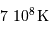 .
.
- Question 5
Aide :
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
Solution :
Un proton 3 fois plus rapide est 9 fois plus énergétique que la moyenne. On gagne donc ainsi un facteur 9 sur la température, soit la possibilité de fusion dès 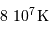 .
.
Ceci reste trop élevé, car la modélisation de l'effet tunnel est trop simpliste, mais montre comment l'estimation purement classique de la température de fusion est déjà surdimensionnée d'un facteur 120.

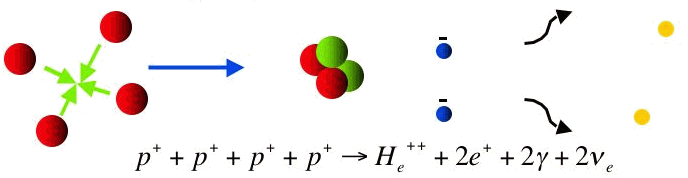
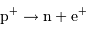 . L'interaction faible mise en jeu induit un très faible taux de réaction.
. L'interaction faible mise en jeu induit un très faible taux de réaction.


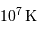 .
.

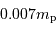 par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de
par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de 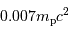 , soit 7 MeV, par nucléon, et a priori de
, soit 7 MeV, par nucléon, et a priori de 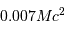 pour toute l'étoile.
pour toute l'étoile.
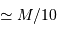 est concernée.
est concernée.
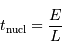
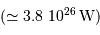 , le taux de conversion par nucléon et la masse concernée donne :
, le taux de conversion par nucléon et la masse concernée donne :
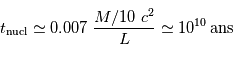
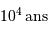 seulement.
seulement.


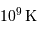 . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
. Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
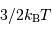 , une proportion non négligeable de protons est sensiblement plus rapide.
, une proportion non négligeable de protons est sensiblement plus rapide.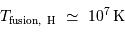
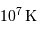 . Au delà de
. Au delà de 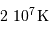 , le cycle CNO est prépondérant.
, le cycle CNO est prépondérant.
 de l'élément considéré :
de l'élément considéré :
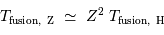

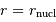
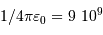 en unité SI, et
en unité SI, et 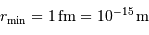 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
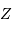 .
.
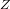 .
.
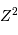
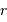 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 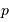 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
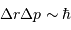
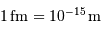
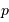 et
et 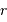 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
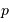 ).
).
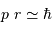
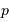 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 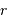 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
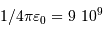 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
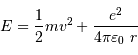
 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
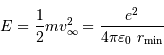
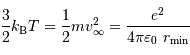
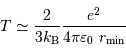
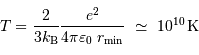
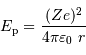
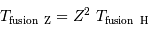
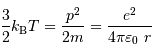
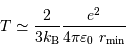
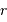 la distance minimale d'approche, et
la distance minimale d'approche, et 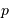 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
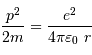
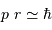 On en déduite la valeur de
On en déduite la valeur de 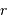 , en éliminant
, en éliminant 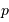 :
:
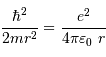
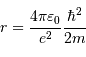
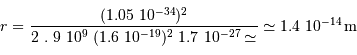
 .
.
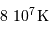 .
.