

 Température de fusion
Température de fusion
Difficulté : ☆☆
Temps : 40 min
Cet exercice a pour but de quantifier, dans un cadre classique, la température minimale qui doit régner au centre d'une étoile pour que s'amorcent les réactions nucléaires. Il se base sur la figure donnant le potentiel d'interaction entre 2 protons.
Question 1)
Mener un bilan d'énergie, pour déterminer l'énergie cinétique minimale conduisant à la fusion.
AideAideSolution
[1 points]
Exprimer l'énergie de la barrière coulombienne.
Exprimer la condition énergétique limite à remplir en 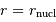
L'énergie totale d'un proton s'écrit :
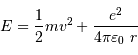
Pour passer la barrière coulombienne en 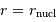 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
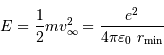
(énergie potentielle nulle à l'infini, énergie cinétique nulle au niveau de la barrière).
Question 2)
En déduire l'expression de la température minimale pour que la fusion puisse avoir lieu.
AideSolution
[2 points]
Faire le lien entre l'énergie cinétique et la température.
La température minimale vérifie :
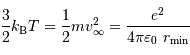
Soit :
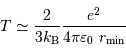
Question 3)
Faire l'application numérique. On donne 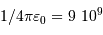 en unité SI, et
en unité SI, et 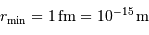 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
Solution
[2 points]
Avec les valeurs proposées, on trouve :
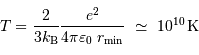
Cette valeur est surestimée, car ne prend pas en compte les phénomènes quantiques qui relaxent considérablement les conditions de fusion.
Question 4)
Comment s'écrit cette température s'il s'agit de faire fusionner non pas 2 protons, mais 2 noyaux d'une élément de charge 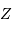 .
.
En déduire que la température de fusion des éléments lourds nécessite une température bien plus élevée que celle pour l'hydrogène.
AideAideSolution
[1 points]
Réécrire le potentiel électrostatique en fonction de 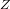 .
.
L'effet varie comme 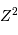
Les équations précédentes se réécrivent avec la nouvelle énergie potentielle
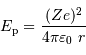
Il s'ensuit une température de fusion :
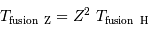
La valeur de la température est encore plus élevée que pour l'hydrogène.

 Du rôle de l'effet tunnel et de la distribution des vitesses
Du rôle de l'effet tunnel et de la distribution des vitesses
Difficulté : ☆☆☆
Temps : 60 min
Sans effet tunnel, la
fusion de l'hydrogène nécessiterait des températures très élevées (et p.ex. non atteintes dans l'intérieur du Soleil). Cet exercice a pour but de décrire le rôle de l'effet tunnel dans le cadre d'un modèle très simplifié.
On note 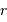 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 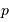 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
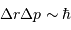
Question 1)
Relier la distance minimale d'approche des 2 protons à la quantité de mouvement incidente, puis à la température du milieu.
AideAideSolution
[1 points]
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
L'exercice consacré à ce raisonnement donne la
solution. Avec les notations ici proposées :
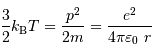
Question 2)
Faire l'application numérique dans le cas d'une distance d'approche de 1 fm, nécessaire pour arriver à une interaction forte entre les protons.
AideSolution
[1 points]
L'application numérique donne :
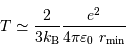
Question 3)
Dans le problème étudié, la loi de distribution des vitesses permet de confondre  et
et 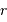 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
On suppose que le proton incident ne sait pas localiser l'autre proton, avec une incertitude dépendant de sa quantité de mouvement incidente précédemment calculée (notée simplement 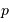 ).
).
Déterminer alors cette incertitude de position.
AideAideSolution
[3 points]
La relation d'incertitude présentée ici se traduit par
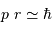
L'égalité entre l'énergie cinétique à grande distance 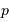 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 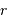 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
En notant simplement 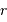 la distance minimale d'approche, et
la distance minimale d'approche, et 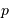 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
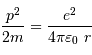
La relation d'incertitude présentée ici se traduit par
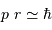 On en déduite la valeur de
On en déduite la valeur de 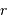 , en éliminant
, en éliminant 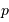 :
:
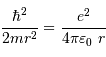
Et donc on aboutit à la nouvelle position (ou incertitude de position, d'après la présentation de l'énoncé) :
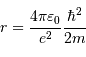
Question 4)
Faire l'application numérique (on donne 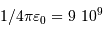 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
Solution
[2 points]
L'application numérique donne :
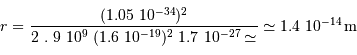
Cette distance est plus grande que 1 fm. Les protons peuvent donc se "tromper", et se croire en train de fusionner alors qu'ils sont 14 fois trop éloignés.
La température de fusion décroît de ce même facteur 14, soit de l'ordre de 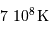 .
.
Question 5)
La distribution des quantités de mouvement assure qu'il existe une population avec des protons 3 fois plus rapide que la valeur moyenne. En déduire la température minimale pour la fusion.
AideSolution
[1 points]
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
Un proton 3 fois plus rapide est 9 fois plus énergétique que la moyenne. On gagne donc ainsi un facteur 9 sur la température, soit la possibilité de fusion dès 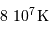 .
.
Ceci reste trop élevé, car la modélisation de l'effet tunnel est trop simpliste, mais montre comment l'estimation purement classique de la température de fusion est déjà surdimensionnée d'un facteur 120.

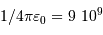 en unité SI, et
en unité SI, et 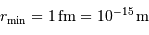 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
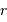 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 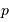 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
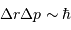
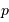 et
et 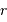 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
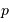 ).
).
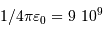 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.