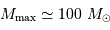Apprendre

Objectifs

Définir dans quelles conditions la fusion de l'hydrogène va s'amorcer.

Prérequis

Pression au centre de l'étoile.

La compression gravitationnelle peut être équilibrée par 3 termes de pression :

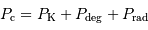
$P _{\mathrm{c}} = P _{\mathrm{K}} + P _{\mathrm{deg}} + P _{\mathrm{rad}}$

respectivement pression du gaz de matière chaud, pression de Fermi et présence du gaz de photons.

Phase de contraction

La compression gravitationnelle au centre de l'objet varie en fonction de sa masse et de son rayon comme :

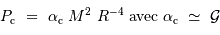
$P _{\mathrm{c}} \ = \ \alpha _{\mathrm{c}}\ M^2\ R^{-4} \mathrm{ \ avec \ } \alpha _{\mathrm{c}} \ \simeq \ {\cal G}$

Lors de la contraction de l'objet, la température centrale varie en fonction du rayon 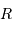comme :

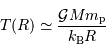
$T(R) \simeq { {\cal G} M m _{\mathrm{p}} \over k _{\mathrm{B}} R}$

(avec 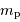$m _{\mathrm{p}}$ la masse du proton). Lorsque 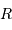décroît, la température augmente, et la pression aussi. La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?

Rôle des différents termes de pression

La pression cinétique présente la même dépendance en masse et rayon que la compression gravitationnelle :

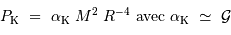
$P _{\mathrm{K}} \ =\ \alpha _{\mathrm{K}}\ M^2 \ R^{-4} \mathrm{ \ avec \ } \alpha _{\mathrm{K}} \ \simeq\ {\cal G}$

Avec ces variables, la pression de dégénérescence varie elle comme :

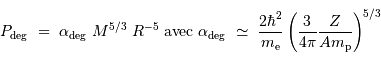
$P _{\mathrm{deg}} \ =\ \alpha _{\mathrm{deg}}\ M^{5/3} \ R^{-5} \mathrm{ \ avec \ } \alpha _{\mathrm{deg}} \ \simeq \ {2\hbar^2 \over m _{\mathrm{e}} }\left({3 \over 4\pi} {Z\over A m _{\mathrm{p}}}\right)^{5/3}$

Lorsque l'objet se contracte, cette pression augmente plus vite que la compression gravitationnelle. Elle peut donc bloquer la compression, en atteignant un équilibre caractérisé par :

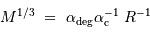
$M^{1/3} \ =\ \alpha _{\mathrm{deg}} \alpha _{\mathrm{c}}^{-1} \ R^{-1}$

Température centrale

Dans ces conditions, la température atteinte au centre vaut (en éliminant la variable rayon des équations qui précèdent) :

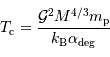
$T _{\mathrm{c}} = { {\cal G}^2 M^{4/3} m _{\mathrm{p}} \over k _{\mathrm{B}} \alpha _{\mathrm{deg}}}$

Si la température centrale atteint 10 millions de Kelvin, une étoile est née. Sinon, il s'agit d'un astre dégénéré sans amorçage des réactions nucléaires.

Masse minimale

Il est nécessaire d'avoir une masse initiale suffisante pour atteindre une température permettant d'initier la fusion de l'hydrogène. Un modèle précis donne la masse minimale pour la combustion de l'hydrogène :

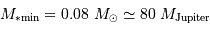
$M _{\mathrm{* min}} = 0.08 \ M_\odot \simeq 80\ M _{\mathrm{Jupiter}}$

Entre 13 et 80 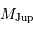$M _{\mathrm{Jup}}$ , l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.

Masse maximale

La pression de radiation varie comme 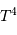T^4 , donc :

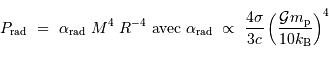
$P _{\mathrm{rad}} \ =\ \alpha _{\mathrm{rad}}\ M^4 \ R^{-4} \mathrm{ \ avec \ } \alpha _{\mathrm{rad}} \ \propto\ {4\sigma \over 3c}\left({ {\cal G} m _{\mathrm{p}}\over 10 k _{\mathrm{B}}}\right)^4$

à comparer à la compression gravitationnelle 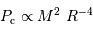$P _{\mathrm{c}} \propto M^2\ R^{-4}$ .

Si la masse est trop importante, la pression de radiation va conduire à souffler l'étoile. La limite d'équilibre 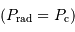$( P _{\mathrm{rad}} = P _{\mathrm{c}})$ est atteinte lorsque :

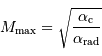
$M _{\mathrm{max}} = \sqrt{\alpha _{\mathrm{c}} \over \alpha _{\mathrm{rad}}}$

Une modélisation précise donne la valeur numérique :

$M _{\mathrm{max}} \simeq 100 \ M_\odot$