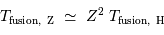Apprendre

Objectifs

Définir dans quelles conditions microphysiques la fusion de l'hydrogène va s'amorcer.

Montrer que la fusion nécessite une température élevée, de l'ordre de 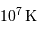$10^7 {\,\mathrm{K}}$ .

Après la phase de contraction

L'examen des constantes de temps dynamiques et de Kelvin Helmholtz a montré que l'effondrement d'un nuage est relativement bref, et que la puissance rayonnée ne va pas durer éternellement.

Energie disponible

La réaction qui de 4 protons conduit à un noyau d'hélium présente un bilan de perte de masse de 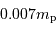$0.007 m _{\mathrm{p}}$ par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de 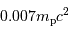$0.007 m _{\mathrm{p}} c^2$ , soit 7 MeV, par nucléon, et a priori de 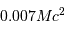0.007 M c^2 pour toute l'étoile.

En fait, seule la région centrale de l'étoile, la plus chaude, permet la fusion. Dans le cas d'une étoile comme le Soleil, seule une masse 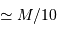$\simeq M/10$ est concernée.

Constante de temps nucléaire

La durée de vie à ce régime, pour une étoile comme le Soleil, est alors :

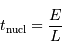
$t _{\mathrm{nucl}} = {E\over L}$

L'application numérique, avec la luminosité solaire mesurée aujourd'hui 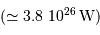$(\simeq 3.8\ 10^{26} {\,\mathrm{W}})$ , le taux de conversion par nucléon et la masse concernée donne :

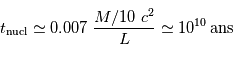
$t _{\mathrm{nucl}} \simeq 0.007\ {M/10\ c^2\over L} \simeq 10^{10} {\,\mathrm{ans}}$

Une réaction chimique, dégageant typiquement 1 eV par nucléon, soit 1 million de fois moins que la fusion de l'hydrogène, conduirait à une durée de vie de 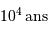$10^4 {\,\mathrm{ans}}$ seulement.

L'estimation de 10 milliards d'année pour le Soleil est très proche de ce que donne une modélisation plus poussée. Actuellement, avec un âge de 4.56 milliards d'années, le Soleil est à mi-parcours sur la séquence principale.

Interagir

Au sein d'une étoile, l'hydrogène est totalement ionisé : la matière se présente sous la forme d'un gaz de protons et d'électrons essentiellement. La réaction entre 2 protons nécessite leur rencontre à très courte distance, car l'interaction nucléaire forte n'a qu'une très courte portée, de l'ordre du femtomètre. Ceci nécessite de vaincre la répulsion électrostatique.

La barrière de potentiel pour une distance de 1 fm entre les 2 protons, peut se traduire en température : de l'ordre de 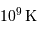$10^9 {\,\mathrm{K}}$ . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.

Deux phénomènes se conjuguent pour faciliter la fusion :

L'effet tunnel conduit à tromper les électrons sur la distance exacte qui les sépare. Il exprime l'incertitude de Heisenberg : les 2 protons fonçant l'un sur l'autre ne peuvent pas avoir une position très précisément définie.
La distribution de vitesse des protons est maxwellienne, donnée par la théorie cinétique du gaz parfait : si l'énergie cinétique moyenne est $3/2 k _{\mathrm{B}} T$ , une proportion non négligeable de protons est sensiblement plus rapide.

Ces points sont quantifiés en exercice.

Fusion de l'hydrogène

En pratique, la température limite de fusion de l'hydrogène est de l'ordre de 10 millions de Kelvin. Pour des températures plus faibles, seule la fusion du deutérium peut s'amorcer.

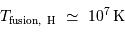
$T _{\mathrm{fusion,\ H}} \ \simeq \ 10^7 {\,\mathrm{K}}$

La fusion par le cycle pp domine lorsque la température n'excède pas 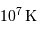$10^7 {\,\mathrm{K}}$ . Au delà de 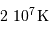$2 \ 10^7 {\,\mathrm{K}}$ , le cycle CNO est prépondérant.

Fusion de noyaux lourds

Plus les noyaux sont lourds, plus leur fusion nécessite une température élevée. En fonction du nombre de charge de l'élément considéré :

$T _{\mathrm{fusion,\ Z}} \ \simeq \ Z^2\ T _{\mathrm{fusion,\ H}}$