Trajectoires balistiques dans le système solaire |
Auteur : Alain Vienne
On considère une sonde spatiale qui se déplace dans le système solaire. On suppose qu'elle ne subit que l'attraction gravitationnelle du Soleil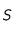 
. Sous cette hypothèse, le mouvement de cette sonde autour du Soleil est un mouvement képlérien c'est-à-dire que la trajectoire est une conique dont le Soleil occupe l'un des foyers.
Les coniques sont des ellipses (comme le dit la première loi de Képler) ou des hyperboles ou des paraboles.
DéfinitionUne conique est l'ensemble des points dont la somme ou la différence, des distances à 2 points fixes est constante. Ces 2 points sont appelés foyers et la distance constante est appelée grand axe
On ne considère pas ici le cas des paraboles qui est le cas limite entre les ellipses et les hyperboles. Une parabole peut être vue comme une ellipse dont l'un des foyer est rejeté à l'infini, ou symétriquement, comme une hyperbole dont l'un des foyers est rejeté à l'infini.
L'exercice proposé considère 2 points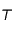 
et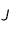 
du système solaire avec 
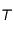plus près de 
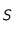que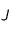 
. On peut considérer que 
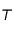est la Terre et que 
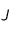est Jupiter. Cela permet de fixer les idées mais il n'y a aucune obligation formelle à cela. On fait partir la sonde du point 
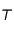pour qu'elle arrive au point 
. 
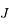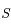étant l'un des foyers, on note 
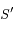le second foyer de la conique 
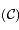qui définit la trajectoire.
 |  |
