Loi normale |
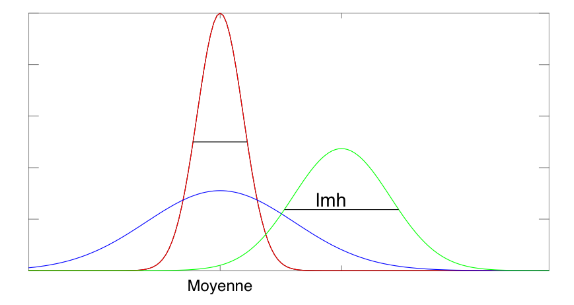
La loi de distribution gaussienne est sans doute la plus employée, en physique comme ailleurs, à tel point qu'on l'appelle généralement loi normale.
La densité de probabilité gaussienne est :
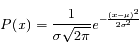
Dans cette formulation, 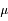 représente la moyenne, et
représente la moyenne, et 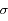 l'écart-type. Le coefficient numérique sert à normaliser l'intégrale à 1.
l'écart-type. Le coefficient numérique sert à normaliser l'intégrale à 1.
On remarque la symétrie de la fonction autour du pic central, et son aspect caractéristique ("en cloche"). On note habituellement N(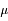 ,
, 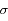 ) la loi normale. N(0,1) est appelée loi normale centrée-réduite (moyenne nulle, variance normalisée à 1).
) la loi normale. N(0,1) est appelée loi normale centrée-réduite (moyenne nulle, variance normalisée à 1).
L'importance de la loi normale est liée au théorème de la limite centrale, qui montre que la superposition de lois de distribution différentes tend vers une loi normale. Ceci est en particulier important pour estimer les erreurs de mesure : si elles sont de provenance différentes, et de statistique mal connue, on peut généralement faire l'approximation que leur somme est distribuée de manière gaussienne. C'est le théorème de la limite centrale qui explique l'omniprésence de la loi normale.