Dérivation de la loi de Poisson
Difficulté : ☆☆
Temps : 40 min
Question 1)
Retrouver la forme générale de la loi de Poisson à partir d'un raisonnement discret.
AideSolution
On découpe la durée considérée en n petits intervalles de temps, et on utilise une loi binomiale.
Le problème est équivalent à calculer la probabilité de trouver k occurrences de l'événement pour n tirages, la probabilité de réalisation durant chaque intervalle étant p = λt/n.
La loi de Bernoulli donne :
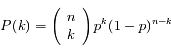
Où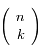 
est le nombre de combinaisons de k éléments parmi n (notation standard moderne).
Pour passer à la limite continue, on prend n → ∞ en gardant pn = λt, et on remarque que :
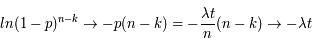
Par ailleurs,
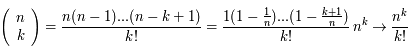
Au total on trouve bien l'expression de la loi de Poisson :
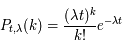
Question 2)
Déterminer la moyenne et l'écart-type de la loi de Poisson.
Solution
Si X est une variable aléatoire discrète suivant une loi de Poisson, sa valeur moyenne s'écrit :
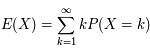
On note ici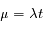 
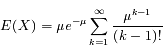
On remarque que la série est le développement de l'exponentielle, il reste :
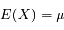
La variance de X s'écrit :
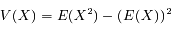
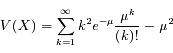
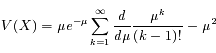
![V(X) = \mu e^{-\mu} \frac{d}{d\mu}[\mu e^{\mu}] - \mu^2](../pages_proba/equations_proba/equation18.png)
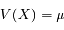
D'où l'écart-type :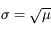 
Question 3)
On observe une source lumineuse faible pendant un temps 
. Quel est le nombre de photons détectés en moyenne, de quoi dépend-il ? Que représente l'écart-type de cette distribution ? Quel paramètre permet de quantifier la précision de la mesure, et comment améliorer la mesure de cette source ?
Solution
Si la fréquence d'émission des photons par la source est λ, le nombre moyen de photons détectés (valeur moyenne du signal) est :
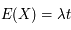
Cette quantité est proportionnelle au temps de pose 
et à la fréquence d'émission.
L'écart-type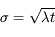 
réprésente la variation moyenne autour de cette valeur moyenne, qu'on observerait par exemple entre des mesures successives. Cette fluctuation est liée au processus d'émission de photons lui-même, pas à la méthode de mesure ; c'est donc une incertitude fondamentale qu'on ne peut pas outrepasser en changeant d'instrument. On l'appelle couramment bruit de photons dans ce cas.
La qualité de la mesure est estimée par le rapport signal sur bruit. Si aucune autre incertitude n'affecte cette mesure, le rapport signal sur bruit est :
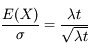
On améliore donc la mesure en posant plus longtemps, mais cette amélioration est lente (en racine de t, voir l'animation ci-dessous).
Remarque
L'applet ci-dessous illustre ce dernier résultat : on améliore le rapport signal sur bruit en posant plus longtemps, mais cette amélioration est lente.
Elle est spectaculaire au début (en permettant la reconnaissance de l'objet), mais ralentit de plus en plus (les détails sont de plus en plus longs à se préciser).
Loi de Poisson
Les événements poissoniens sont ici des impacts de photons sur un détecteur CCD. L'image se forme au fur et à mesure que le nombre de détections augmente : elle devient de moins en moins bruitée et donc plus lisible.
