On observe un astéroïde de la ceinture principale avec un télescope de 2 m depuis le sol. Le fond de ciel produit un signal de 100 pas-codeurs à la sortie de la caméra. A quel niveau de signal peut-on penser avoir détecté l'objet ?
Un télescope de cette taille n'est pas normalement équipé d'un dispositif d'optique adaptative. La résolution angulaire est donc limitée par la turbulence atmosphérique, et à cette distance l'objet apparaît quasiment ponctuel.
Le signal total en provenance de l'objet est donc concentré sur quelques pixels (la taille de la tache de diffraction). Il est à comparer avec le niveau du ciel et ses fluctuations.
Le niveau du fond de ciel suit une loi de Poisson. Les fluctuations associées sont donc en racine de N, soit un écart-type de 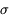 =10 pas-codeurs. Selon la règle énoncée plus haut, l'objet sera considéré comme détecté si un niveau supérieur à 3
=10 pas-codeurs. Selon la règle énoncée plus haut, l'objet sera considéré comme détecté si un niveau supérieur à 3 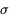 = 30 pas-codeurs est mesuré au dessus du signal moyen (100 pas-codeurs) sur un pixel du champ : on n'a en effet que 3 chances sur mille d'obtenir un tel niveau comme réalisation d'un tirage aléatoire gaussien.
= 30 pas-codeurs est mesuré au dessus du signal moyen (100 pas-codeurs) sur un pixel du champ : on n'a en effet que 3 chances sur mille d'obtenir un tel niveau comme réalisation d'un tirage aléatoire gaussien.
Cependant, on a dans ce cas de très nombreux pixels (on utilise typiquement des détecteurs de 500x500), et donc un nombre significatif de pixels à 3 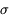 (750 en moyenne dans ce cas). Ce qui facilite la détection est le fait que l'image d'un objet ponctuel est une tache étendue sur le détecteur ; les observations significativement au-dessus du fond de ciel sont donc groupées spatialement, ce qui permet de les repérer facilement. Outre le rapport signal sur bruit, la largeur à mi-hauteur (LMH) de cette tache est donc également un critère de détection important.
(750 en moyenne dans ce cas). Ce qui facilite la détection est le fait que l'image d'un objet ponctuel est une tache étendue sur le détecteur ; les observations significativement au-dessus du fond de ciel sont donc groupées spatialement, ce qui permet de les repérer facilement. Outre le rapport signal sur bruit, la largeur à mi-hauteur (LMH) de cette tache est donc également un critère de détection important.
Détection à 5 sigma, LMH = 1.5 pixels

Image 512x512 avec un fond poissonien à 100 pas-codeurs. Selon le critère usuel, on a ici une détection extrêmement bonne : à 5
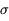
, étendue sur une dizaine de pixels voisins. Saurez-vous trouver l'astéroïde ?
Détection 5 sigma, lmh = 2 pixels

Dans le cas où la tache de diffaction est légèrement plus grande, l'identification visuelle devient relativement aisée.
Remarque : attention, dans les deux exemples ci-dessus le niveau de la source (l'intégrale du signal sur tous les pixels de la tâche de diffraction) est différent. Dans le deuxième exemple, la source est plus étalée mais en fait beaucoup plus brillante (le niveau maximum est identique malgré l'étalement du signal). Si on dégrade la résolution en sommant sur des boîtes larges de quelque lmh, on revient à une situation où l'on peut comparer l'écart avec la loi normale ; mais on voit que le critère à 3 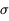 est généralement insuffisant pour ce type d'application.
est généralement insuffisant pour ce type d'application.


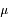 > 5).
> 5).