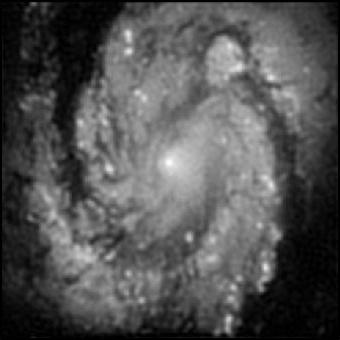
Ex: Filtrage de Wiener

L'image reçue par le CCD est une collection de pixels que l'on rassemble sous la forme d'un vecteur 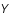. Ce vecteur resulte de l'image initiale, 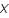, qui a été convoluée par le télescope auquel s'ajoute un vecteur bruit noté 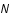. La convolution se modélise par l'application d'une matrice 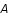sur le vecteur 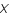. Ainsi on a: 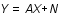. Dans l'espace de Fourier, cette relation s'ecrit: 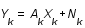où 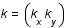représente la fréquence spatiale en deux dimensions. Dans cet espace, la matrice 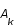est diagonale de valeur propre 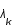. 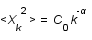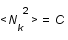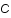Le spectre de puissance de l'image suit souvent une loi de puissance, c'est à dire et le bruit est souvent un bruit blanc c'est à dire qu'il à la même intensité quelquesoit la fréquence spatiale, , où et 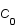sont des constantes. Montrer que l'inversion simple de cette relation (qui consiste à appliquer la matrice 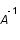sur les données 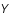afin de retrouver 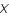) conduit, au delà d'une certaine fréquence, à une amplification du bruit.

Galaxie spirale M100

Image convoluée bruitée

Solution

En inversant on obtient . Comme le spectre de puissance de l'image decroit quand augmente et que celui du bruit reste constant, il existe une fréquence limite à partir delaquelle et donc le bruit est amplifié et domine la reconstruction de l'image.

Image déconvoluée

On cherche donc maintenant à déconvoluer l'image mais aussi à filtrer le bruit. Pour cela, on va chercher le filtre 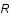à appliquer sur les données 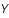qui va minimiser l'écart quadratique moyen entre la vraie image 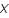et l'image filtrée 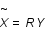. On cherche donc à minimiser la quantité 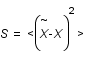par rapport à 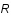. 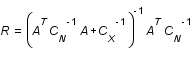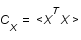En postulant que le bruit et le signal sont décorrélés et que le bruit est non biaisé (pas d'erreur systématique), montrer que ,où et 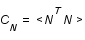sont les matrices de variance-covariance du signal et du bruit.

AideSolution

Dans l'espace de Fourier, les matrices de variance-covariance sont diagonales également et se réduisent aux spectres de puissances. Montrer que le filtre de Wiener 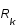inverse les basses fréquences et coupe les plus grandes où le bruit domine.

Image déconvoluée filtrée

Solution