Variations du champ magnétique
Pour les calculs qui suivent sur le mouvement du
centre guide, on orientera localement (en un
point
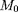
autour duquel tourne la particule) le repère
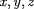
de telle sorte que l'axe

soit parallèle à la direction du champ magnétique
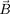
. Comme les variations du champ magnétique sont
faibles (
12,
14,
15), on peut décrire le champ
magnétique à l'aide d'un développement
limité du premier ordre au voisinage du
point
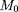
autour duquel tourne la particule, et au voisinage
du temps
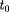
. Pour alléger un peu, on convient que
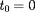
et
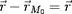
:
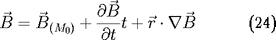
où le gradient du champ magnétique
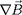
est le tenseur défini par
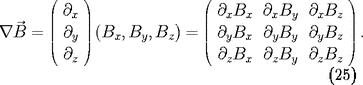
Il serait tentant d'annuler les deux premières lignes
puisque
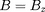
en
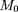
. Que nenni ! Ce n'est pas parce que des fonctions
s'annulent en un point que leurs dérivées s'annulent
aussi. En particulier, l'existence possible
de
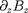
combinée avec la relation
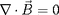
implique des termes comme
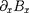
ou
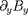
donc l'existence de composantes
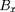
ou
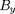
dès que l'on s'éloigne du point
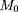
. On pourra développer le champ électrique de
manière analogue :
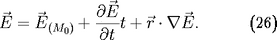
Par souci d'alléger les notations, on omettra les
indices
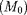
, sauf de temps en temps pour éviter une confusion
possible. Pour bien comprendre, il suffit de se dire
dans ce qui suit que toutes les grandeurs de
champs qui apparaissent sont définies au
point
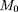
et au temps

et que ce sont donc des grandeurs constantes.

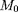 autour duquel tourne la particule) le repère
autour duquel tourne la particule) le repère
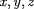 de telle sorte que l'axe
de telle sorte que l'axe
 soit parallèle à la direction du champ magnétique
soit parallèle à la direction du champ magnétique
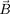 . Comme les variations du champ magnétique sont
faibles (12,14,15), on peut décrire le champ
magnétique à l'aide d'un développement
limité du premier ordre au voisinage du
point
. Comme les variations du champ magnétique sont
faibles (12,14,15), on peut décrire le champ
magnétique à l'aide d'un développement
limité du premier ordre au voisinage du
point
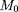 autour duquel tourne la particule, et au voisinage
du temps
autour duquel tourne la particule, et au voisinage
du temps
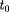 . Pour alléger un peu, on convient que
. Pour alléger un peu, on convient que
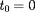 et
et
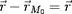 :
: 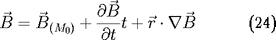
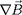 est le tenseur défini par
est le tenseur défini par 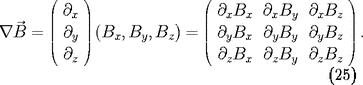
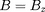 en
en
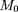 . Que nenni ! Ce n'est pas parce que des fonctions
s'annulent en un point que leurs dérivées s'annulent
aussi. En particulier, l'existence possible
de
. Que nenni ! Ce n'est pas parce que des fonctions
s'annulent en un point que leurs dérivées s'annulent
aussi. En particulier, l'existence possible
de
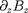 combinée avec la relation
combinée avec la relation
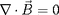 implique des termes comme
implique des termes comme
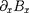 ou
ou
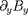 donc l'existence de composantes
donc l'existence de composantes
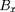 ou
ou
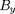 dès que l'on s'éloigne du point
dès que l'on s'éloigne du point
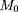 . On pourra développer le champ électrique de
manière analogue :
. On pourra développer le champ électrique de
manière analogue : 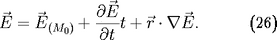
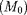 , sauf de temps en temps pour éviter une confusion
possible. Pour bien comprendre, il suffit de se dire
dans ce qui suit que toutes les grandeurs de
champs qui apparaissent sont définies au
point
, sauf de temps en temps pour éviter une confusion
possible. Pour bien comprendre, il suffit de se dire
dans ce qui suit que toutes les grandeurs de
champs qui apparaissent sont définies au
point
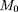 et au temps
et au temps
 et que ce sont donc des grandeurs constantes.
et que ce sont donc des grandeurs constantes.