Comment on trouve la formule du courant de magnétisation
Voici une démonstration de
22. On part de
l'équation d'Ampère
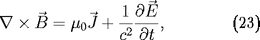
mais on aimerait bien l'exprimer seulement à partir
du courant porté par les centre guides (c'est à dire
calculé avec la vitesse
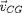
) au lieu de la vitesse totale
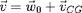
de la particule. Pour cela, on calcule à part la
contribution au courant de la vitesse de
giration
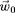
. Au lieu de calculer le courant de manière
directe, on va calculer de champ magnétique
moyen
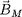
engendré par le petit circuit électrique que
constitue la particule en mouvement circulaire de
vitesse
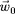
. Le rotationnel de ce champ nous donnera le
courant, qu'on appelle courant de magnétisation.
Le courant électrique instantané du circuit crée par
la particule en rotation est
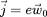
. Le champ magnétique
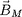
associé à ce courant vérifie
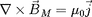
, le flux de ce champ à travers le disque défini par
la trajectoire de la particule est
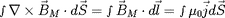
. Ce champ
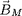
est parallèle et de sens opposé au champ
magnétique ambiant
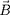
. En moyennant sur une giropériode,
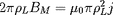
, en tenant compte de la définition du rayon de
Larmor
10, du moment magnétique
 18
18 de la particule, et de la valeur
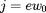
, on obtient la relation simple
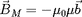
où
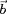
est la direction du champ magnétique ambient. Le
courant équivalent est
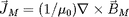
d'où
22. Le courant de magnétisation est un
courant moyen, sur des durées excédant la
giropériode.

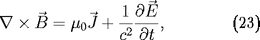
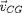 ) au lieu de la vitesse totale
) au lieu de la vitesse totale
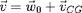 de la particule. Pour cela, on calcule à part la
contribution au courant de la vitesse de
giration
de la particule. Pour cela, on calcule à part la
contribution au courant de la vitesse de
giration
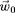 . Au lieu de calculer le courant de manière
directe, on va calculer de champ magnétique
moyen
. Au lieu de calculer le courant de manière
directe, on va calculer de champ magnétique
moyen
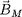 engendré par le petit circuit électrique que
constitue la particule en mouvement circulaire de
vitesse
engendré par le petit circuit électrique que
constitue la particule en mouvement circulaire de
vitesse
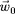 . Le rotationnel de ce champ nous donnera le
courant, qu'on appelle courant de magnétisation.
Le courant électrique instantané du circuit crée par
la particule en rotation est
. Le rotationnel de ce champ nous donnera le
courant, qu'on appelle courant de magnétisation.
Le courant électrique instantané du circuit crée par
la particule en rotation est
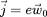 . Le champ magnétique
. Le champ magnétique
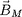 associé à ce courant vérifie
associé à ce courant vérifie
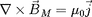 , le flux de ce champ à travers le disque défini par
la trajectoire de la particule est
, le flux de ce champ à travers le disque défini par
la trajectoire de la particule est
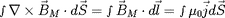 . Ce champ
. Ce champ
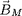 est parallèle et de sens opposé au champ
magnétique ambiant
est parallèle et de sens opposé au champ
magnétique ambiant
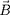 . En moyennant sur une giropériode,
. En moyennant sur une giropériode,
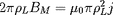 , en tenant compte de la définition du rayon de
Larmor 10, du moment magnétique
, en tenant compte de la définition du rayon de
Larmor 10, du moment magnétique
 18 de la particule, et de la valeur
18 de la particule, et de la valeur
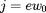 , on obtient la relation simple
, on obtient la relation simple
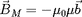 où
où
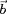 est la direction du champ magnétique ambient. Le
courant équivalent est
est la direction du champ magnétique ambient. Le
courant équivalent est
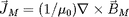 d'où 22. Le courant de magnétisation est un
courant moyen, sur des durées excédant la
giropériode.
d'où 22. Le courant de magnétisation est un
courant moyen, sur des durées excédant la
giropériode.