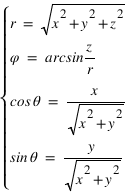Se positionner dans l'espace |
Pour se positionner dans l’espace, il convient d’ajouter une troisième dimension. Tout ce que nous avons dit pour les repères à deux dimensions se transpose pour les repères à trois dimensions.
La figure suivante représente un repère orthonormé direct, le troisième axe est l’axe Oz.
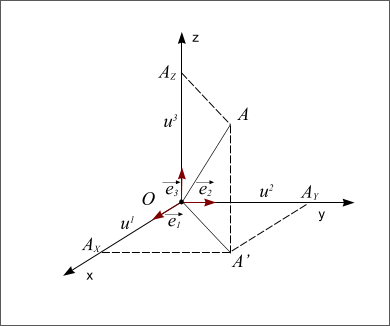
Le point A est projeté orthogonalement en A’ sur le plan Oxy, puis A’ est projeté en AX sur l’axe Ox et en AY sur l’axe Oy. Le point A est également projeté orthogonalement en AZ sur l’axe Oz. Les coordonnées 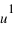 ,
,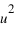 et
et 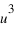 du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire :
du point A sont les coordonnées axiales des projections du point A sur les trois axes. On peut écrire : 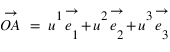 , les coordonnées
, les coordonnées 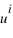 sont appelées coordonnées contravariantes du vecteur
sont appelées coordonnées contravariantes du vecteur 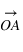 (ou projections parallèles). Elles sont souvent notées (x,y,z).
(ou projections parallèles). Elles sont souvent notées (x,y,z).
On peut substituer à ces coordonnées un jeu de coordonnées polaires formé de deux angles (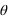 ,
,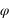 ) et une distance
) et une distance 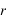 . L’angle
. L’angle 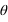 est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle
est l’angle entre la projection OA’ de OA dans le plan (Oxy) et l’axe Ox. L’angle 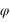 est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
est l’angle entre OA et sa projection OA’. r est la distance entre l’origine O est le point A.
On passe des coordonnées polaires (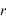 ,
,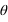 ,
,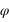 ) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
) aux coordonnées cartésiennes (x,y,z) grâce aux relations suivantes :
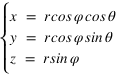
Inversement on passe des coordonnées cartésiennes aux coordonnées polaires par les relations suivantes :