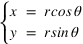Translation de repère

Changement d’origine d’un repère

L'usage de repère cartésien est très répandu, on l'utilise systématiquement lorsque l'on trace un graphique. Il est souvent intéressant de pouvoir déplacer le repère sans pour autant changer l'orientation de ses deux axes. On dit alors que le repère est en translation. Pour un point quelconque du plan, on distingue deux possibilités :

• Le point A est lié au repère, dans ce cas la position du point A dans le repère translaté est la même.
• Le point A n'est pas lié au repère, dans ce cas le point A ne se déplace pas avec le repère et ses coordonnées dans le repère translaté ne sont plus les mêmes.

Figure 5 : Point A lié au repère translaté

Figure 5 : Point A lié au repère translaté.

Crédit : ASM/Patrick Rocher

Figure 6 : Point A non lié au repère tranlaté.

Figure 6 : Point A non lié au repère translaté.

Crédit : ASM/Patrick Rocher

Rotation de repère

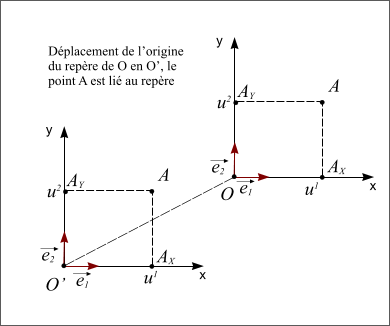
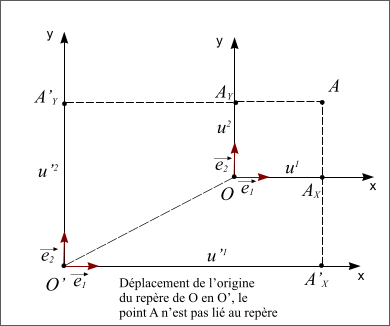
On peut également faire tourner le repère autour de son origine O, dans ce cas on peut également distinguer les points liés au repère qui vont tourner avec lui (dans ce cas leurs coordonnées ne changeront pas) et les points non liés au repère qui ne tourneront pas avec lui (dans ce cas leurs coordonnées vont changer).

Coordonnées polaires

On peut également utiliser un système de coordonnées polaires défini par deux coordonnées : la distance 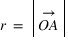du point A au centre O du repère et l’angle entre la direction OA et l’un des axes. L'angle est compté positivement dans le sens direct (sens inverse des aiguilles d'une montre), souvent à partir de l'axe Ox

Dans ce cas on passe des coordonnées cartésiennes (x,y) aux coordonnées polaires (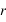,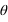) par les relations mathématiques suivantes : 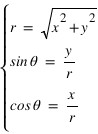Les deux dernières relations peuvent être remplacées par 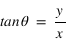, mais l'on doit alors choisir le bon angle 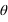et fonction des signes 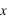de et de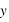

Et inversement on passe des coordonnées polaires aux coordonnées cartésiennes par les relations :