 |  |  |  |  |  |
Se positionner dans le plan |
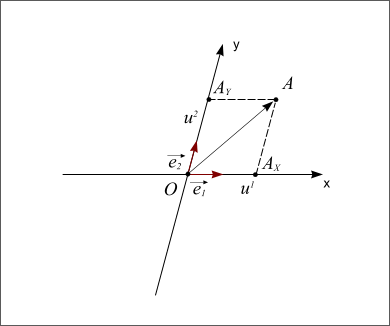
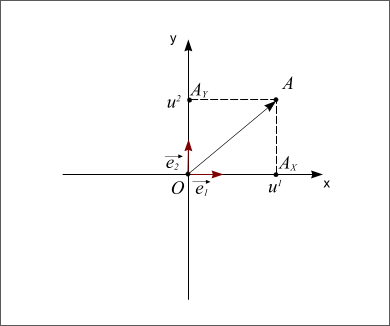
Pour pouvoir se positionner dans le plan, on doit définir un repère ayant la même dimension que le plan : la dimension deux. Pour cela on utilise deux vecteurs unitaires notés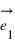 
et 
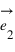ayant la même origine O, ces deux vecteurs ne doivent pas être co-linaires, c'est-à-dire que les droites qui les supportent ne doivent pas être confondues ou parallèles.
Pour connaître la position d'un point A dans le plan par rapport au repère défini par les deux vecteurs, on va projeter le point A sur l'axe portant le vecteur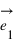 
parallèlement à la droite portant le vecteur 
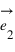; et sur l'axe portant le vecteur 
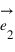parallèlement à la droite portant le vecteur 
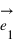. Les coordonnées 
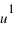et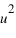 
du point A sont les coordonnées axiales des projections du point A sur les deux axes. On peut écrire : 
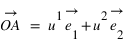, les coordonnées 
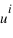sont appelées coordonnées contravariantes du vecteur (ou projections parallèles). Elles sont souvent notées (x,y).
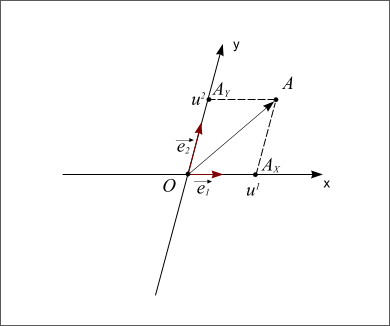
Si les deux vecteurs sont perpendiculaires, le repère est dit orthogonal. Si les deux vecteurs ont la même longueur, on dit que le repère est normé. Et si les deux vecteurs sont perpendiculaires et s'ils ont la même longueur alors le repère est dit orthonormé. L'axe Ox porte le nom d'axe des abscisses et l'axe Oy porte le nom d'axe des ordonnées. Enfin si l'on passe de l'axe Ox à l'axe Oy par une rotation dans le sens inverse des aiguilles d'une montre (sens trigonométrique ou sens direct) on dit que le repère est direct. Dans le cas inverse, le repère est dit indirect.
 |  |
