La notion de repère cartésien

Nous vivons et nous observons dans un espace à trois dimensions. Toute étude de mouvement dans notre environnement demande de positionner les corps par rapport à un repère de dimension trois. Le but du présent chapitre est de rappeler les notions de repère dans l'espace et les méthodes mathématiques qui permettent de changer de type de repère. On n'abordera pas dans ce chapitre la notion d'espace relativiste qui introduit le temps local comme quatrième dimension.

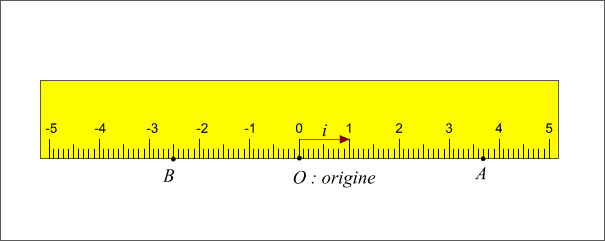
On remarquera que nous n'avons pas indiqué d'unité de mesure sur le dessin, l'unité de mesure est la longueur du vecteur 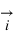, ce vecteur porte donc le nom de vecteur unitaire.

On peut également écrire que 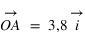et que .

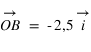On remarquera également que chaque point de l'axe a une coordonnée et qu'inversement à chaque coordonnée correspond un point de l'axe. Cette propriété mathématique, appelée bijection entre le droite et l’ensemble des nombres réels, est fondamentale, car c’est elle qui permet de faire de la géométrie analytique.

Nota Bene : En mathématiques, le mot espace n'a pas le sens courant. Le 'plan' courant est un espace à 2 dimensions en mathématique et l''espace' courant est un espace à 3 dimensions en mathématiques. Il n'y a pas de mot courant pour les espaces à 4 (et plus) dimensions.