Apprendre

Objectifs

Identifier un objet via une propriété caractéristique peut permettre la détermination de sa magnitude absolue, et donc de sa distance.

Prérequis

Module de distance

Les céphéides

Les étoiles céphéides sont des étoiles pulsantes dont la luminosité varie périodiquement au cours du temps. Elles tiennent leur nom de l'étoile 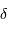$\delta$ Céphée, identifiée en 1784 par John Goodricke.

En étudiant les céphéides du Petit Nuage de Magellan, Henrietta Leavitt découvrit en 1912 que la période de variation de leur éclat apparent est corrélée à leur magnitude absolue moyenne.

Les étoiles du Petit Nuage de Magellan étant toutes à la même distance de nous, leur éclat apparent (magnitude apparente 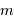) est donc un indicateur de leur luminosité intrinsèque (magnitude absolue 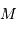) par la relation :

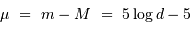
$\mu\ =\ m-M\ =\ 5 \log d -5$

où la distance est exprimée en parsec.

L'étalonnage absolu de la relation période - luminosité

La relation énoncée par H. Leavitt est de la forme :

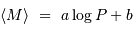
$\langle M\rangle \ =\ a \log{P} +b$

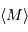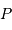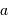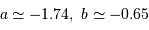avec $\langle M\rangle$ la valeur moyenne de la magnitude absolue et la période. Comme le coefficient est négatif, plus une céphéide est lumineuse, plus sa période est longue. Pour les céphéides de type I, $a\simeq -1.74, \ b\simeq -0.65$ .

La relation admise aujourd'hui s'exprime avec les coefficients suivants, pour diverses bandes (B, V, I) :

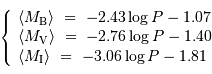
$\left\lbrace \begin{array}{l} \langle M _{\mathrm{B}}\rangle \ =\ -2.43 \log{P} - 1.07 \\ \langle M _{\mathrm{V}}\rangle \ =\ -2.76 \log{P} - 1.40 \\ \langle M _{\mathrm{I}}\rangle \ =\ -3.06 \log{P} - 1.81 \end{array} \right.$

Cette relation constitue bien un indicateur de distance puisque la mesure de la période 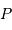permet de déterminer 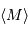$\langle M\rangle$ et donc la distance par comparaison avec la magnitude apparente médiane. La pente de la relation pouvait être établie avec les céphéides du Petit Nuage de Magellan, mais la détermination du coefficient 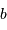, qui fixe le point zéro de la relation nécessite un étalonnage avec des céphéides de distances connues. Cet étalonnage fut réalisé par E. Hertzsprung en 1913, puis par H. Shapley en 1918 en utilisant une population de céphéides observées dans des amas globulaires de notre Galaxie. Quand, en 1924, Edwin Hubble mesure pour la première fois des céphéides dans M31, puis M33 et NGC6822, il utilisa cet étalonnage pour déterminer leurs distances.

Les caractéristiques des Céphéides
	Type 1	Type 2
Type	F - G	F-G
Classe	Ia	Ia
période	de 3 à 50 j	de 5 à 30 j
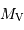$M _{\mathrm{V}}$	de -2 à -6	de 0 à -2
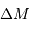$\Delta M$	de 0 à -6	de 0 à -4

Les distances mesurables

Les céphéides ont l'avantage d'être intrinsèquement très lumineuses et donc de pouvoir être observées à grande distance (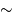 $\sim$ 25 Mpc avec le télescope spatial Hubble). Leur mécanisme de pulsation est de plus physiquement bien connu, ce qui en fait un indicateur de distance très fiable. Ces étoiles sont observables essentiellement dans les galaxies spirales ou irrégulières, où il existe des populations stellaires jeunes.

Le mécanisme des céphéides

Les céphéides sont des étoiles en phase de combustion centrale de l'hélium. Lorsque l'étoile entre dans la phase d'instabilité, ses couches externes sont soumises à de légères variations de pression. Une compression conduit à l'ionisation du gaz, en particulier l'hélium présent proche de la surface. Or l'hélium ionisé est très opaque au rayonnement et agit donc comme un écran, qui, poussé par la pression de radiation, fait gonfler l'enveloppe de l'étoile comme un ballon.

La luminosité de l'étoile est fonction à la fois de sa température superficielle et de son rayon d'après la loi de rayonnement du corps noir. Quand l'enveloppe enfle, la surface émettrice augmente. En se détendant, l'enveloppe se refroidit et les ions d'hélium se recombinent avec les électrons. L'atmosphère redevient alors perméable aux photons et retombe vers l'étoile.

L'accroissement du rayon et la baisse de température induisent des effets opposés pour ce qui est de la luminosité. En pratique, les variations de rayon et température sont en quadrature, et la luminosité est en phase avec la température.

La durée de vie d'une céphéide dans cet état d'oscillation est de l'ordre de un million d'années. La plupart des étoiles entre 3 et 15 masses solaires passent par cette phase. Les étoiles les plus massives ont les périodes les plus longues : ayant un rayon plus important, elles mettent plus de temps à se dilater.