S'évaluer

La distance de l'amas de la Vierge et le télescope spatial Hubble

Difficulté : ☆☆ Temps : 45 min

On se propose de calculer la distance de l'amas de galaxies de La Vierge en utilisant des mesures de céphéides obtenues avec le télescope spatial.

Nom	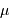$\mu$	site
NGC 4321	31.15	HST
NGC 4496A	31.13	HST
NGC 4639	32.00	HST
NGC 4536	31.10	HST
NGC 4571	30.76	Sol

La table ci-jointe fournit, pour 5 galaxies attribuées à l'amas de La Vierge, les modules de distance déterminés par les céphéides, ainsi que la provenance de la mesure (HST ou terrestre). Par ailleurs, on connaît la valeur moyenne des vitesses radiales observées de l'amas :

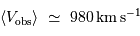
$\langle V _{\mathrm{obs}}\rangle\ \simeq\ 980 {\,\mathrm{km\,s}}^{-1}$

et la vitesse de chute de notre Groupe Local de galaxies en direction de l'amas de La Vierge :

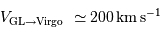
$V_{\mathrm{GL}\to\mathrm{Virgo}}\ \simeq 200 {\,\mathrm{km\,s}}^{-1}$

Question 1)

Déterminer la distance des objets de cet amas. Semble-t-il ramassé ou étendu ?

[3 points]

Question 2)

On cherche à déterminer la valeur moyenne de la distance de cet amas, qui présente une grande extension. Montrer que l'identification des céphéides favorise la détection des composantes les plus proches. Quel biais cela peut-il introduire ?

[1 points]

Question 3)

Calculer la valeur moyenne de la distribution des distances.

[0.5 points]

Question 4)

En appliquant la loi de Hubble, déduire une estimation de la constante d'expansion de l'Univers 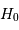H_0 .

[1 points]

Les globules dans la nébuleuse autour de la céphéide RS Pup

Difficulté : ☆☆ Temps : 45 min

La céphéide RS Pup est entourée d'une nébuleuse circumstellaire, qu'elle éclaire. Les courbes de lumières des globules dans cette nébuleuse présentent la même périodicité que celle de la céphéide, mais avec un retard dû à la propagation de la lumière de l'étoile aux globules. Ce délai se traduit par un déphasage de leur courbe de lumière. Les globules très proches du plan perpendiculaire à la ligne de visée ont été sélectionnés : ils apparaissent sur les "coquilles" de la nébuleuse entourant la céphéide. La période de la céphéide, mesurée suite aux observations régulières sur la céphéide, vaut P = 41.4389 j.

L'exercice se propose de reprendre les travaux d'un groupe d'astronomes, principalement de l'Observatoire de Paris, qui ont abouti à la mesure de la distance de cette étoile. Ces mesures effectuées en 2007 constituent à ce jour la mesure de distance la plus précise pour une céphéide.

Question 1)

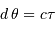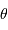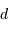Montrer que la distance linéaire entre RS Pup et un globule s'écrit : $d\, \theta = c \tau$ avec $\theta$ la distance angulaire observée entre l'étoile et le globule, et la distance du système par rapport au Soleil. Pourquoi n'a-t-on sélectionné que des globules dans le plan perpendiculaire à la ligne de visée ?

Aide [2 points]

Question 2)

Montrer que l'on peut écrire 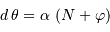$d\, \theta = \alpha\ (N+\varphi)$ , avec 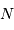un entier et 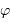$\varphi$ la phase du signal, exprimée en fraction de période. Exprimer le facteur 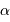$\alpha$ en fonction de la période 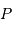de la céphéide, puis le calculer pour une distance 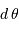$d\, \theta$ exprimée en UA.

Aide Aide [1 points]

Question 3)

Montrer que la phase 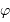$\varphi$ peut être mesurée, mais que le nombre entier 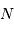de périodes reste a priori inconnu.

Aide [1 points]

Question 4)

L'appliquette ci-jointe donne, pour les globules sélectionnés, les mesures de 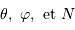$\theta, \ \varphi, \ \mathrm{et} \ N$ . Le nombre 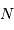a été retrouvé par essai/erreur sur quelques valeurs. Déduire alors de la nouvelle appliquette la distance 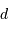(en prenant soin d'éliminer l'une des mesures qui apparaît visiblement contradictoire avec les autres). Montrer qu'elle est directement donnée en parsec. 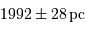Est-elle compatible avec la valeur rapportée par les auteurs de ce travail : $1992\pm 28 {\,\mathrm{pc}}$ ?

Aide Aide [2 points]