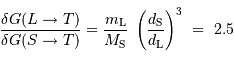Le phénomène des
marées est abordé dans le cadre très simplifié d'un modèle statique. Ce modèle, incapable de prédire l'heure et la hauteur d'une marée dans votre port préféré, est néanmoins en mesure de dévoiler le principe du phénomène.
Deux situations sont abordées :
- Les marées sur Terre, décrites à l'aide du modèle de l'océan global
- Les marées sur les satellites.
Il est important de comprendre que le champ de marée est un
champ différentiel, qui agit sur la structure d'un corps non ponctuel.
Pour en savoir plus : voir le site du
SHOM (Service
Hydrographique et Océanographique de la Marine), qui propose par
exemple un modèle de calcul de marée.
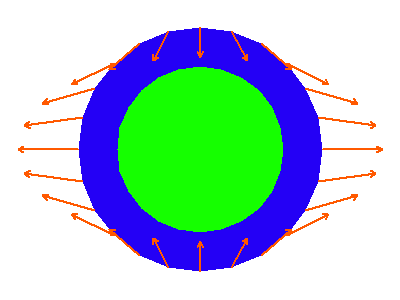
Le champ de marée de la Lune sur la Terre (modèle statique) .
Crédit :
ASM
Lune et marée
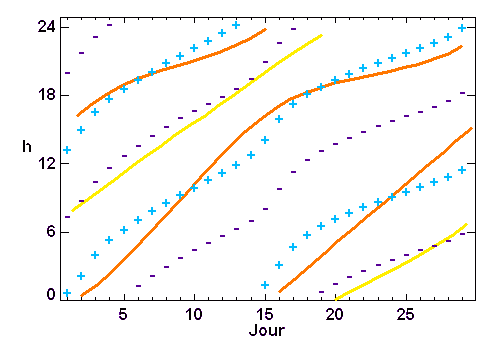
Evolution des horaires des marées à Saint-Malo, pour le mois de septembre 2002, calculés par le SHOM.
La courbe jaune représente le passage de la Lune au
méridien, et les 2 courbes rouges les levers et couchers de la Lune. Les + et les - signalent respectivement les horaires des marées hautes et basses.
Les horaires des marées, environ 2 hautes et 2 basses par jour, suivent clairement ceux de la Lune.
Crédit :
SHOM et ASM
Lunaisons et marées
L'examen des horaires de marée montre une nette corrélation entre l'orbite de la Lune et la marée.
Ceci apparaît sur la figure ci-jointe,
qui montre comment évoluent les horaires des marées hautes et basses, en fonction des levers et couchers de la Lune.
Le phasage précis des marées avec la Lune est complexe, comme le montre la suite.
Phases de la Lune et coefficients de marée
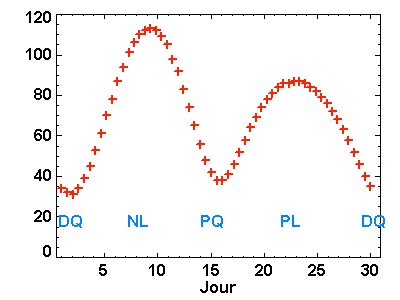
L'évolution du coefficient de marée, pour le mois de septembre 2002, calculée par le SHOM, marque une forte corrélation avec les phases de la Lune : les marées sont plus marquées aux environs des nouvelle et pleine lunes.
Crédit :
SHOM et ASM
Grandes marées et phases de la Lune
Le coefficient de marée, qui sur une échelle relative de 20 à 120, mesure l'amplitude de la marée, apparaît également corrélé à la Lune, à ses phases en fait.
Approche statique
Dans l'approche statique, développée plus loin, on ne s'intéresse pas à la dynamique de l'écoulement des eaux océaniques, mais seulement au champ de force qui crée la marée.
L'approche statique met en évidence le rôle joué par la Lune sur le champ de marée, et explique la périodicité des marées (de l'ordre de 12h25min).
Approche dynamique
Si l'approche statique permet de comprendre le phénomène des marées, elle
est notoirement insuffisante pour calculer la hauteur de marée en un lieu
donné. Un tel calcul nécessite :
- Une approche dynamique.
- Une modélisation précise de la topographie locale.
Les coefficients de marée
On définit usuellement des coefficients de marée, sur une échelle de 20
(marée minimale, dite de morte-eau, d'amplitude 1.22 m à Brest) à 120 (marée maximale, dite de vive-eau, d'amplitude 7.32 m à Brest).
L'approche statique permet de comprendre que :
- Les maxima ont lieu aux nouvelle et pleine lunes
- Les minima ont lieu aux quartiers
En revanche, le phasage entre les courbes de marée et la course
lunaire n'est pas direct. Ce n'est pas étonnant : la mise en mouvement
des masses océaniques n'est pas immédiate, et ces dernières ne peuvent pas suivre instantanément, c'est à dire sans déphasage, la phase de l'excitation. On peut aussi noter qu'à la résonance, un système excité n'est pas en phase avec l'excitateur, mais en quadrature.
Coefficients de marée
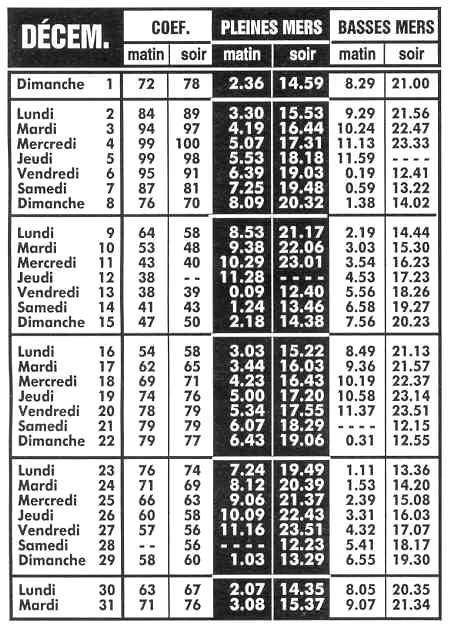
Coefficients de marées en décembre 2002.
Crédit :
SHOM
Les grandes marées
Les plus fortes marées sont observées aux équinoxes. Deux raisons à cela :
- C'est aux équinoxes que le forçage des marées est le plus régulier,
car la Lune comme le Soleil sont respectivement levés et couchés 12 h.
- Aux équinoxes, la Lune et le Soleil passent par le plan équatorial terrestre.
Lune et marée
Les phénomènes de marée ont été étudiés depuis l'Antiquité (en particulier par les Grecs et les Romains). Dès 350 avant notre ère, Aristote attribuait les marées à la Lune et au Soleil, ceux-ci attirant l'eau des mers.
Pline l'Ancien énonce au 1er siècle dans son Histoire Naturelle :
"Sur la nature des eaux, enfin, beaucoup a déjà été dit; mais cette avance et le retrait des flots sont les plus extraordinaires; cependant si ce phénomène offre beaucoup de variété, sa cause réside dans le Soleil et dans la Lune". Il observe les deux marées par jour : "Entre deux levers de la Lune, la mer monte deux fois et redescend deux fois dans chaque intervalle de 24 heures" puis il remarque que "Jamais les marées ne se reproduisent au même moment que le jour précédent, comme si elles haletaient par la faute de l'astre avide qui attire à lui les mers pour s'abreuver".
Il décrit également fort bien le décalage de temps entre les pleines mers et le passage au méridien de la Lune "les phénomènes célestes faisant toujours sentir leurs effets à la Terre avec du retard sur la vue, comme l'éclair, le tonnerre ou la foudre", il décrit la corrélation entre les marées de vives-eaux et les syzygies et entre les marées de mortes-eaux et les quadratures "Au moment de la conjonction, elles égalent les marées de pleine Lune".
Diverses théories
Si les faits observationnels semblaient clairs, le mécanisme moteur des marée a dû attendre Newton pour commencer à être dévoilé. Auparavant, c'est plutôt le principe de sympathie qui prévaut : l'eau de la Lune (!) attire l'eau de la Terre.
Galilée propose un modèle en analogie avec un pendule.
Descartes (1596 - 1650) apporte une explication cohérente, qui relie les astres par de la matière et les fait se déplacer par des tourbillons. La Lune comprime la matière du ciel, qui écrase l'eau.
Modèle de l'océan global

Le modèle : un océan global.
Crédit :
ASM
Effet de marée, exemple sur Terre
En ayant remarqué qu'une flaque d'eau ne subit pas de marée, serait-elle aussi grande que le Lac Léman, on s'intéressera à la marée à l'échelle planétaire, en allant jusqu'à supposer la présence d'un océan global couvrant uniformément toute la Terre. Une description plus précise des marées en un lieu donné du globe nécessite un cadre plus précis. Selon le lieu, les phénomènes de
marée peuvent présenter des aspects fort différents, non abordés dans ce
cours : la topographie des lieux, associée au phénomène de résonance, permet de comprendre les grandes marées rencontrées p.ex. dans la baie du Mont-Saint-Michel.
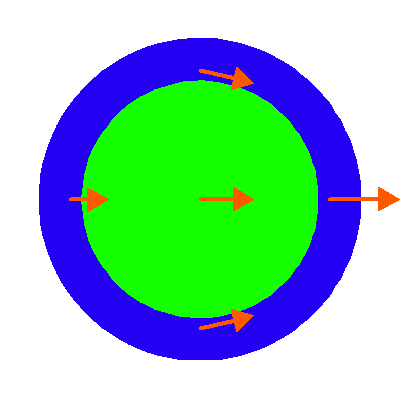
Dans un référentiel galiléen, le champ de gravité de la Lune en chaque point de la Terre est représenté par des vecteurs dirigés vers le centre de la Lune, de module inversement variable par rapport au carré de l'éloignement (échelle non respectée) (modèle statique).
Crédit :
ASM
Du fait de sa masse, la Lune crée un champ gravitationnel dont l'intensité est d'autant plus faible que la distance à la Lune est grande. L'action de ce champ en chaque point de la Terre crée une force dirigée vers le centre de gravité de la Lune.
Pour comprendre l'action du champ gravitationnel de la Lune sur la
Terre, on se place dans un référentiel quasi géocentrique, mais
tournant avec la Lune.
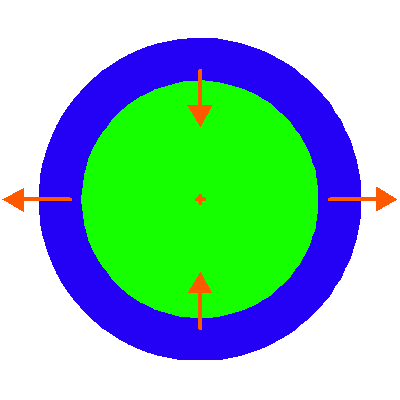
Le champ de marée apparaît dans le référentiel barycentrique de la Terre. (modèle statique).
Crédit :
ASM
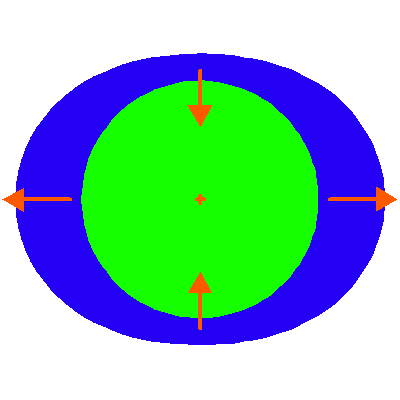
La face faisant face à la Lune est soumise à un champ gravitationnel lunaire plus important que le centre de la Terre. On y observe une marée haute.
La face la plus éloignée subissant un champ moins important que le centre, une marée haute y a lieu également (modèle statique).
Crédit :
ASM
Dans le référentiel barycentrique de la Terre
Dans le référentiel terrestre, le centre de la Terre est au repos, les bourrelets de marée sont fixes, en permanence pointés vers la Lune. Sous ces bourrelets fixes, la Terre défile. Elle tourne en 24h50, soit la période synodique de la Lune. Autrement dit, dans le référentiel terrestre, on voit passer 2 marées hautes par 24h50.
Le champ de marée
Le champ de marée en un point du globe évolue en fonction de la phase de la Lune et de la rotation terrestre.

Le champ de marée lunaire provoque 2 bourrelets de l'océan. Dans le
cadre d'un modèle statique, ces bourrelets suivent rigoureusement la
Lune. La rotation de la Terre est modélisée par un rayon vecteur tournant rouge (modèle statique).
Crédit :
ASM
Dans un modèle dynamique, plus réaliste, il y a un décalage entre la position de la Lune et la marée.
 Périodicité des marées
Périodicité des marées
Difficulté : ☆☆
Temps : 30 min
Le but de cet exercice est de calculer la période des marées sur Terre.
La période de révolution de la Lune autour de la Terre dépend du référentiel de l'observateur. C'est pourquoi on définit une période de révolution sidérale, 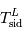 et une période de révolution synodique,
et une période de révolution synodique, 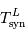 . La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (
. La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (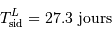 ). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
La marée haute est en permanence dirigée vers la Lune.
Question 1)
D'où provient la différence entre les deux périodes ? Expliquez avec un schéma.
[2 points]
Question 2)
Connaissant 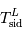 , calculer
, calculer 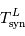 .
.
[2 points]
Le changement de référentiel donne, pour la composition des vitesses angulaires :
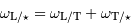
donc
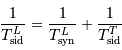
Question 3)
Pourquoi est-il utile de connaître la période de rotation propre de la Terre vue depuis la Lune ? On appellera 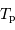 cette période.
cette période.
[1 points]
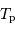 est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
Question 4)
Calculer 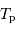 .
.
[1 points]
Procéder comme pour le calcul de 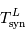 .
.
Composition des vitesses angulaires :
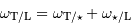
Question 5)
Quelle est la périodicité des marées hautes?
[2 points]
 Horaires et coefficients des marées
Horaires et coefficients des marées
Difficulté : ☆
Temps : 20 min
Le tableau ci-joint fournit les horaires et coefficients des marées sur 1 mois.
Coefficients de marée

Exemple d'horaires et de coefficients de marée.
Crédit :
SHOM
Question 1)
Déterminer à l'aide du graphe la période des marées.
[2 points]
Question 2)
Pourquoi certains jours n'y a-t-il qu'une seule marée haute ou qu'une seule marée basse ?
[2 points]
La marée haute suit la position apparente de la Lune ; marée haute et basse s'alternent rapidement, essentiellement à cause du mouvement de rotation propre de la Terre. Les coefficients de marée sont plus forts dans les conditions d'alignement du Soleil et du couple Terre-Lune, donc aux nouvelle et pleine lunes (modèle statique). Dans un modèle dynamique (plus réaliste), il y a un décalage entre la position de la lune et la marée.
Crédit :
ASM
Bourrelets (é)mouvants
Les animations, dans le cadre d'une théorie statique de la marée et du modèle de l'océan global, montrent comment les
bourrelets de la marée suivent la course de la Lune autour de la Terre.
Horaires de la Lune et des marées

La courbe jaune représente le passage de la Lune au
méridien, et les 2 courbes rouges les levers et couchers de la Lune. Les + et les - signalent respectivement les horaires des marées hautes et basses.
Le modèle statique prévoit la concordance entre marée haute et passage de la Lune au méridien (modulo 12h25), et marée basse et lever ou coucher de la Lune. Ce n'est visiblement pas le cas : les phénomènes dynamiques gouvernent la ... dynamique des marées.
Crédit :
SHOM et ASM
L'approche statique en défaut
L'approche statique suppose que les masses océaniques réagissent instantanément au champ de marée, ce qui n'est pas vrai, comme cela apparaît sur les prévisions. Les conditions géographiques locales entraînent un horaire des marées également local.
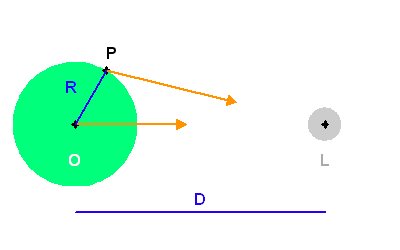
Définitions des distances
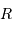
et
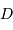
.
Crédit :
ASM
Les forces de marée sont des forces différentielles
La Terre n'est pas un point, mais a une dimension finie. Or l'intensité du champ gravitationnel de la Lune varie comme l'inverse du carré de la distance à la Lune. Il en résulte une attraction différentielle qui déforme la Terre.
On peut estimer la valeur du champ de marée 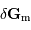 dans le cadre du modèle de l'océan global. On démontre que le module de
dans le cadre du modèle de l'océan global. On démontre que le module de 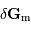 est de l'ordre de
est de l'ordre de 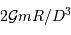
Il ressort de cette analyse que l'effet de marée :
 Marée dans une flaque d'eau
Marée dans une flaque d'eau
Difficulté : ☆☆
Temps : 30 min
Question 1)
On exprime l'ordre de grandeur du module du champ de marée 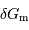 de la Lune sur la Terre de la façon suivante :
de la Lune sur la Terre de la façon suivante :
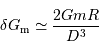
avec 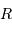 le rayon de la Terre,
le rayon de la Terre, 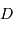 , la distance Terre-Lune (
, la distance Terre-Lune (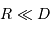 ), et
), et 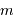 la masse de la Lune.
la masse de la Lune.
Dans le modèle de l'océan global, caractérisé par une distance 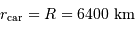 mesurant l'étendue d'eau, la hauteur
mesurant l'étendue d'eau, la hauteur 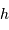 de la
marée est de l'ordre de 1 m.
de la
marée est de l'ordre de 1 m.
En supposant que 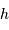 est, comme le champ de marée, une fonction
linéaire de
est, comme le champ de marée, une fonction
linéaire de 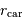 , estimer la hauteur de marée dans les cas suivants :
, estimer la hauteur de marée dans les cas suivants :
- une mer s'étendant sur 640 km,
- un lac s'étendant sur 64 km,
- une flaque d'eau de 64 cm.
En déduire pourquoi il n'y a pas de marée dans une flaque d'eau, ni même dans un grand lac.
[2 points]
Il s'agit d'une règle de trois.
Quadrature

Lors du premier et du dernier quartier de Lune, on observe des marées de faible amplitude dites de morte-eau. Les contributions du Soleil (bleu foncé) et de la Lune (bleu ciel) étant en quadrature (modèle statique).
Crédit :
ASM
Conjonction

Lors de la pleine lune ou de la nouvelle lune, on observe des marées de grande amplitude dites de vive-eau, les contributions du Soleil et de la Lune se superposant en phase (modèle statique).
Crédit :
ASM
Marées de vive-eau et de morte-eau
Le Soleil, la Terre et la Lune sont en
quadrature quand les
axes Lune-Terre et Terre-Soleil sont perpendiculaires. Les effets
conjugués de la Lune et du Soleil s'opposent.
Le Soleil, la Terre et la Lune, en
conjonction, sont
alignés. Les champs de marée de la Lune et du Soleil s'ajoutent.
Dans les 2 cas, la marée due à la Lune reste plus forte que celle
due au Soleil (voir exercice ci-dessous).
Il faut aussi garder en tête le décalage entre la position de la Lune et la marée dû aux forces de frottement dans la planète et les océans en particulier.
La contribution du Soleil dans les marées
On a pu remarquer que les champs de marée sont proportionnelles à la masse de l'astre perturbateur d'une part, et inversement proportionnelles au cube de la distance avec l'astre perturbateur.
Il s'ensuit que la Terre est soumise principalement au champ gravitationnel de la Lune. Bien que plus massif, le Soleil a une influence moindre sur les eaux de nos océans!
Toutefois, le Soleil n'a pas une influence nulle sur les marées. Pour certaines configurations, les champs de marée du Soleil et de la Lune s'ajoutent (marées de vive-eau), et pour d'autres, se retranchent (marées de morte-eau).
Le champ de marée : Lune et Soleil
Le champ de marée en un point du globe évolue en fonction de la phase de la Lune et de la
rotation terrestre.

Evolution du champ de marée, dans le cadre de l'approche statique et du modèle de l'océan global, en fonction de la phase de la Lune (modèle statique).
Crédit :
ASM
 L'influence du Soleil sur les marées
L'influence du Soleil sur les marées
Difficulté : ☆
Temps : 15 min
On se propose de calculer l'influence relative
du Soleil sur les marées par rapport à celle de la Lune.
Question 1)
Exprimer les valeurs des champs de marées 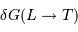 de la Lune sur la Terre et
de la Lune sur la Terre et 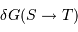 du Soleil sur la Terre
du Soleil sur la Terre
[1 points]
Se référer au cours, qui montre que l'effet de marée est un effet différentiel.
- Question 1
Aide :
Lien vers la page sur les périodes sidérale et synodique .
Solution :
La Lune tourne autour de la Terre en 27.3 jours. Mais la Terre tourne autour du Soleil, donc il faut à la Lune un peu plus de temps pour finir une période apparente.
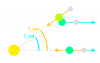
- Question 2
Aide :
Jeter un coup d'oeil à la page concernant les changements de référentiel
Aide :
Le changement de référentiel donne, pour la composition des vitesses angulaires :
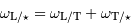
donc
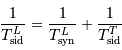
Solution :
Le changement de référentiel donne :
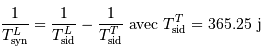
On en déduit :
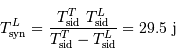
- Question 3
Aide :
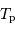 est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
Solution :
Cela permet de prévoir l'heure des marées.
- Question 4
Aide :
Procéder comme pour le calcul de 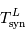 .
.
Aide :
Composition des vitesses angulaires :
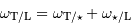
Solution :
De la même façon que l'on a calculé 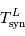 :
:
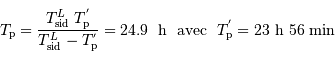
soit 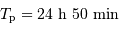 .
.
- Question 5
Solution :
Il y a 2 marées hautes par jour, et donc on observe une marée haute toutes les 12h 25min.









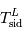 et une période de révolution
et une période de révolution 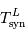 . La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (
. La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (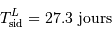 ). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
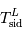 , calculer
, calculer 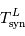 .
.
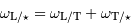
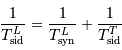
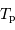 cette période.
cette période.
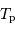 est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
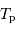 .
.
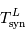 .
.
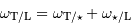

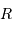 et
et 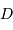 .
.
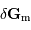 dans le cadre du modèle de l'océan global. On démontre que le module de
dans le cadre du modèle de l'océan global. On démontre que le module de 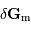 est de l'ordre de
est de l'ordre de 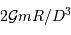
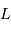 en un point courant
en un point courant 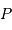 du globe terrestre, que l'on repère par rapport au
centre
du globe terrestre, que l'on repère par rapport au
centre 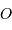 de la Terre.
On note
de la Terre.
On note 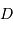 la distance
la distance 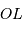 , et
, et 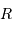 le rayon terrestre.
La composante du champ de marée
le rayon terrestre.
La composante du champ de marée 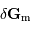 en
en 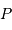 représente la différence du champ lunaire
entre les points
représente la différence du champ lunaire
entre les points 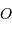 et
et 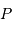 . Les calculs sont menés au 1er ordre par rapport au petit terme
. Les calculs sont menés au 1er ordre par rapport au petit terme 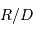 (car
(car 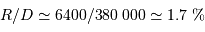 ) :
) :
![\begin{eqnarray*} \delta \mathbf{G} _{\mathrm{m}} &=& {{\cal G} m} { {\mathbf{PL}} \over PL^{3}} - {{\cal G} m} { {\mathbf{OL}} \over OL^{3}} \\ &=& {{\cal G} m} \left[{ {\mathbf{PO}}+ {\mathbf{OL}} \over PL^{3}} - { {\mathbf{OL}} \over OL^{3}} \right]\\ &\simeq& {{\cal G} m} \left[ { {\mathbf{PO}} \over {D}^{3}} + { {\mathbf{OL}} \over PL^{3}} - { {\mathbf{OL}} \over {D}^{3}} \right]\\ \end{eqnarray*}](../pages_maree-terrestre/equations_approche-statique/equation18.png)
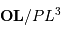 de l'équation précédente, en injectant la relation de Chasles
de l'équation précédente, en injectant la relation de Chasles 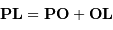 , et toujours au premier ordre en
, et toujours au premier ordre en 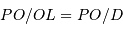 :
:
![\begin{eqnarray*} { {\mathbf{OL}} \over PL^{3}}&=& { {\mathbf{OL}} \over [{ {\mathbf{PL}}^{2}}]^{3/2}}= { {\mathbf{OL}} \over [( {\mathbf{PO}}+ {\mathbf{OL}})^{2}]^{3/2}}\\ \\ &\simeq& { {\mathbf{OL}} \over {D}^{3} \left( 1 + 2\ {\mathbf{PO}} . {\mathbf{OL}} / {D}^{2} \right)^{3/2}}\\ &\simeq& { {\mathbf{OL}} \over {D}^{3}} \left(1 - 3\ {\mathbf{PO}} . {\mathbf{OL}} / {D}^{2} \right)\\ \end{eqnarray*}](../pages_maree-terrestre/equations_approche-statique/equation22.png)
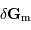 , en introduisant les
vecteurs unitaires
, en introduisant les
vecteurs unitaires 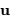 et
et 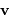 tels que
tels que 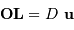 et
et 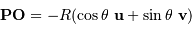 :
:
![\begin{eqnarray*} \delta \mathbf{G} _{\mathrm{m}} &=& {{\cal G} m} \left[ { {\mathbf{PO}} \over {D}^{3}} - {3\ {\mathbf{PO}} . {\mathbf{OL}} \over {D}^{2}}\ { {\mathbf{OL}} \over {D}^{3}} \right]\\ &=& {{\cal G} m\over {D}^{3}} \left[-R\ (\cos\theta\ \mathbf{u} + \sin\theta\ \mathbf{v}) + 3 R\ \cos\theta\ \mathbf{u} \right]\\ &=& {{\cal G} m R\over {D}^{3}} \left[2 \cos \theta\ \mathbf{u} - \sin \theta\ \mathbf{v} \right]\\ \end{eqnarray*}](../pages_maree-terrestre/equations_approche-statique/equation28.png)
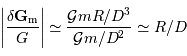
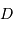 au corps provoquant la marée.
au corps provoquant la marée.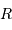 de l'objet affecté.
de l'objet affecté.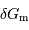 de la Lune sur la Terre de la
de la Lune sur la Terre de la 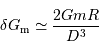
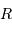 le rayon de la Terre,
le rayon de la Terre, 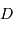 , la distance Terre-Lune (
, la distance Terre-Lune (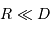 ), et
), et 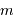 la masse de la Lune.
la masse de la Lune.
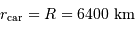 mesurant l'étendue d'eau, la hauteur
mesurant l'étendue d'eau, la hauteur 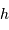 de la
marée est de l'ordre de 1 m.
de la
marée est de l'ordre de 1 m.
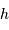 est, comme le champ de marée, une fonction
linéaire de
est, comme le champ de marée, une fonction
linéaire de 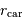 , estimer la hauteur de marée dans les cas suivants :
, estimer la hauteur de marée dans les cas suivants :
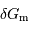 de la
Lune sur la Terre.
de la
Lune sur la Terre.
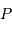 et
et 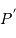 de la Terre, tels que
de la Terre, tels que 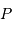 ,
, 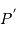 et
et 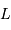 soient alignés, le point
soient alignés, le point 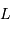 repérant le centre de la Lune.
Soit
repérant le centre de la Lune.
Soit 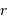 la distance
la distance 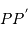 , et
, et 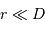 .
.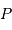 et
et 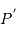 de façon à bien caractériser le problème.
de façon à bien caractériser le problème.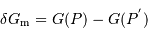 , en effectuant un développement limité au 1er ordre en
, en effectuant un développement limité au 1er ordre en 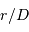 .
.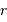 vaut
vaut 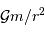 .
.
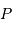 ou
ou 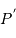 a intérêt à être confondu avec le centre de la Terre.
a intérêt à être confondu avec le centre de la Terre.



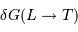 de la Lune sur la Terre et
de la Lune sur la Terre et 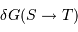 du Soleil sur la Terre
du Soleil sur la Terre
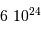
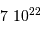
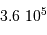
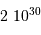
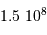
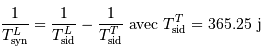
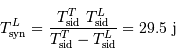
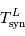 :
:
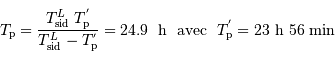
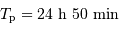 .
.
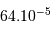
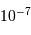
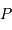 (centre de laTerre) :
(centre de laTerre) :
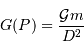
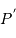 , côté opposé à la Lune. En ce point,
, côté opposé à la Lune. En ce point, 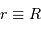 , et :
, et :
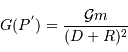
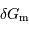 est alors:
est alors:
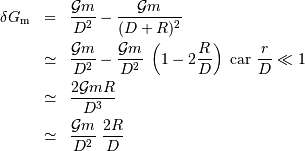
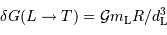 .
.
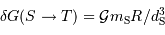 .
.