Lune et marée
Les phénomènes de marée ont été étudiés depuis l'Antiquité (en particulier par les Grecs et les Romains). Dès 350 avant notre ère, Aristote attribuait les marées à la Lune et au Soleil, ceux-ci attirant l'eau des mers.
Pline l'Ancien énonce au 1er siècle dans son Histoire Naturelle :
"Sur la nature des eaux, enfin, beaucoup a déjà été dit; mais cette avance et le retrait des flots sont les plus extraordinaires; cependant si ce phénomène offre beaucoup de variété, sa cause réside dans le Soleil et dans la Lune". Il observe les deux marées par jour : "Entre deux levers de la Lune, la mer monte deux fois et redescend deux fois dans chaque intervalle de 24 heures" puis il remarque que "Jamais les marées ne se reproduisent au même moment que le jour précédent, comme si elles haletaient par la faute de l'astre avide qui attire à lui les mers pour s'abreuver".
Il décrit également fort bien le décalage de temps entre les pleines mers et le passage au méridien de la Lune "les phénomènes célestes faisant toujours sentir leurs effets à la Terre avec du retard sur la vue, comme l'éclair, le tonnerre ou la foudre", il décrit la corrélation entre les marées de vives-eaux et les syzygies et entre les marées de mortes-eaux et les quadratures "Au moment de la conjonction, elles égalent les marées de pleine Lune".
Diverses théories
Si les faits observationnels semblaient clairs, le mécanisme moteur des marée a dû attendre Newton pour commencer à être dévoilé. Auparavant, c'est plutôt le principe de sympathie qui prévaut : l'eau de la Lune (!) attire l'eau de la Terre.
Galilée propose un modèle en analogie avec un pendule.
Descartes (1596 - 1650) apporte une explication cohérente, qui relie les astres par de la matière et les fait se déplacer par des tourbillons. La Lune comprime la matière du ciel, qui écrase l'eau.
Modèle de l'océan global

Le modèle : un océan global.
Crédit :
ASM
Effet de marée, exemple sur Terre
En ayant remarqué qu'une flaque d'eau ne subit pas de marée, serait-elle aussi grande que le Lac Léman, on s'intéressera à la marée à l'échelle planétaire, en allant jusqu'à supposer la présence d'un océan global couvrant uniformément toute la Terre. Une description plus précise des marées en un lieu donné du globe nécessite un cadre plus précis. Selon le lieu, les phénomènes de
marée peuvent présenter des aspects fort différents, non abordés dans ce
cours : la topographie des lieux, associée au phénomène de résonance, permet de comprendre les grandes marées rencontrées p.ex. dans la baie du Mont-Saint-Michel.
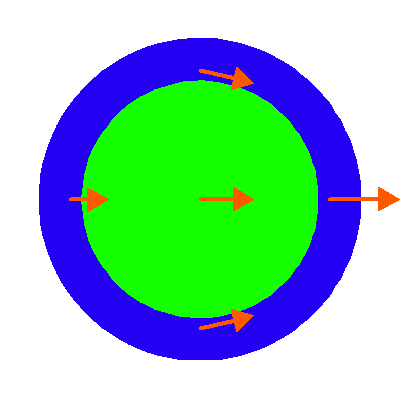
Dans un référentiel galiléen, le champ de gravité de la Lune en chaque point de la Terre est représenté par des vecteurs dirigés vers le centre de la Lune, de module inversement variable par rapport au carré de l'éloignement (échelle non respectée) (modèle statique).
Crédit :
ASM
Du fait de sa masse, la Lune crée un champ gravitationnel dont l'intensité est d'autant plus faible que la distance à la Lune est grande. L'action de ce champ en chaque point de la Terre crée une force dirigée vers le centre de gravité de la Lune.
Pour comprendre l'action du champ gravitationnel de la Lune sur la
Terre, on se place dans un référentiel quasi géocentrique, mais
tournant avec la Lune.
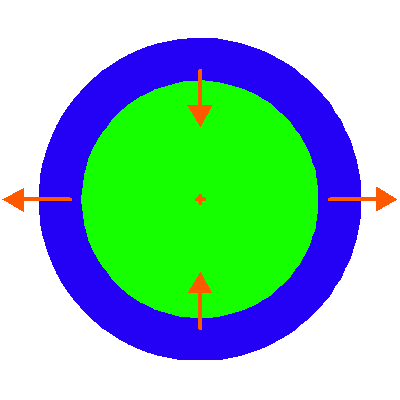
Le champ de marée apparaît dans le référentiel barycentrique de la Terre. (modèle statique).
Crédit :
ASM
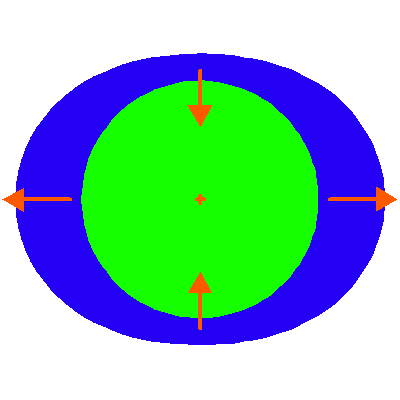
La face faisant face à la Lune est soumise à un champ gravitationnel lunaire plus important que le centre de la Terre. On y observe une marée haute.
La face la plus éloignée subissant un champ moins important que le centre, une marée haute y a lieu également (modèle statique).
Crédit :
ASM
Dans le référentiel barycentrique de la Terre
Dans le référentiel terrestre, le centre de la Terre est au repos, les bourrelets de marée sont fixes, en permanence pointés vers la Lune. Sous ces bourrelets fixes, la Terre défile. Elle tourne en 24h50, soit la période synodique de la Lune. Autrement dit, dans le référentiel terrestre, on voit passer 2 marées hautes par 24h50.
Le champ de marée
Le champ de marée en un point du globe évolue en fonction de la phase de la Lune et de la rotation terrestre.

Le champ de marée lunaire provoque 2 bourrelets de l'océan. Dans le
cadre d'un modèle statique, ces bourrelets suivent rigoureusement la
Lune. La rotation de la Terre est modélisée par un rayon vecteur tournant rouge (modèle statique).
Crédit :
ASM
Dans un modèle dynamique, plus réaliste, il y a un décalage entre la position de la Lune et la marée.
 Périodicité des marées
Périodicité des marées
Difficulté : ☆☆
Temps : 30 min
Le but de cet exercice est de calculer la période des marées sur Terre.
La période de révolution de la Lune autour de la Terre dépend du référentiel de l'observateur. C'est pourquoi on définit une période de révolution sidérale, 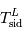 et une période de révolution synodique,
et une période de révolution synodique, 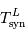 . La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (
. La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (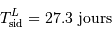 ). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
La marée haute est en permanence dirigée vers la Lune.
Question 1)
D'où provient la différence entre les deux périodes ? Expliquez avec un schéma.
[2 points]
Question 2)
Connaissant 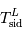 , calculer
, calculer 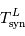 .
.
[2 points]
Le changement de référentiel donne, pour la composition des vitesses angulaires :
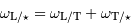
donc
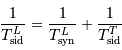
Question 3)
Pourquoi est-il utile de connaître la période de rotation propre de la Terre vue depuis la Lune ? On appellera  cette période.
cette période.
[1 points]
 est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
Question 4)
Calculer 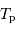 .
.
[1 points]
Procéder comme pour le calcul de 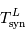 .
.
Composition des vitesses angulaires :
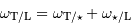
Question 5)
Quelle est la périodicité des marées hautes?
[2 points]
 Horaires et coefficients des marées
Horaires et coefficients des marées
Difficulté : ☆
Temps : 20 min
Le tableau ci-joint fournit les horaires et coefficients des marées sur 1 mois.
Coefficients de marée
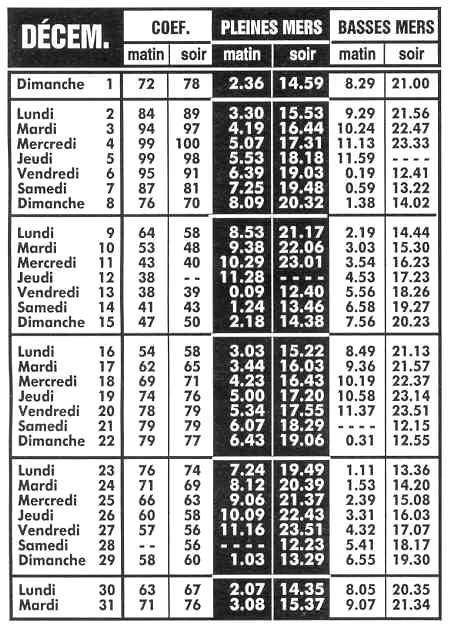
Exemple d'horaires et de coefficients de marée.
Crédit :
SHOM
Question 1)
Déterminer à l'aide du graphe la période des marées.
[2 points]
Question 2)
Pourquoi certains jours n'y a-t-il qu'une seule marée haute ou qu'une seule marée basse ?
[2 points]
- Question 1
Aide :
Lien vers la page sur les périodes sidérale et synodique .
Solution :
La Lune tourne autour de la Terre en 27.3 jours. Mais la Terre tourne autour du Soleil, donc il faut à la Lune un peu plus de temps pour finir une période apparente.
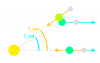
- Question 2
Aide :
Jeter un coup d'oeil à la page concernant les changements de référentiel
Aide :
Le changement de référentiel donne, pour la composition des vitesses angulaires :
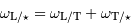
donc
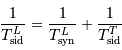
Solution :
Le changement de référentiel donne :
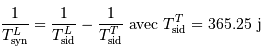
On en déduit :
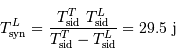
- Question 3
Aide :
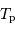 est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
Solution :
Cela permet de prévoir l'heure des marées.
- Question 4
Aide :
Procéder comme pour le calcul de 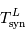 .
.
Aide :
Composition des vitesses angulaires :
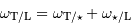
Solution :
De la même façon que l'on a calculé 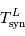 :
:
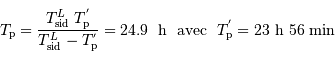
soit 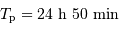 .
.
- Question 5
Solution :
Il y a 2 marées hautes par jour, et donc on observe une marée haute toutes les 12h 25min.
 Prérequis
Prérequis




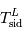 et une période de révolution
et une période de révolution 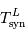 . La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (
. La première, vue des étoiles, est la durée mise par la Lune pour faire un tour complet autour de la Terre (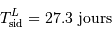 ). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
). La deuxième, vue de la Terre, est la durée entre deux pleines lunes.
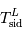 , calculer
, calculer 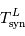 .
.
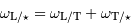
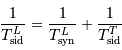
 cette période.
cette période.
 est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
est la durée mise par la Terre pour faire un tour sur elle-même pour un observateur placé sur la Lune.
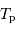 .
.
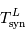 .
.
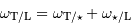

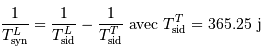
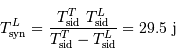
 :
:
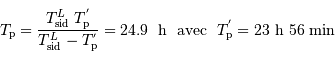
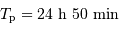 .
.