 |  |  |  |  |  |
Soleil Terre Lune Phénomènes Récurrences des éclipses de Soleil Les périodes de récurrences des éclipsesEn savoir plus: Décomposition d'un réel en fractions continues-2 |
En savoir plusOn obtient des approximations successives de r au moyen de rapports d'entiers en tronquant le développement de la fraction à des ordres plus ou moins élevés que l'on appelle les réduites d'ordre n :
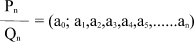
On passe de l'ordre n et n-1 à l'ordre n+1 par la relation de récurrence du second ordre suivante :
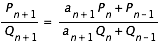
Ces formules de récurrence permettant ce calcul furent découvertes par le mathématicien Indien Bhascara II au début du XIIIe siècle, soit 5 siècles avant que le mathématicien Anglais John Wallis ne les redécouvre en Europe.
Exemple
représentation du nombre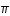 
On a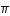 
= 3,141592654
Sa forme réduite d'ordre 4 s'écrit : (3;7,15,1,293)
Les approximations successives sont : 3, 22/7, 333/106, 355/113, 104348/33215.
 |  |