Mesure de la distance Terre-Lune avec la troisième loi de Kepler

La distance moyenne Terre-Lune peut également être déduite par la gravitation. Connaissant le rayon de la Terre par la méthode d'Érathostène (R_T ≈ 6 400 km) et la valeur de l'accélération de la pesanteur à la surface de la Terre (g = 9,78 m.s^-2 à l'équateur), on peut en déduire la valeur de la constante GM par la formule .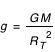

En supposant que la masse de la Lune est négligeable devant celle de la Terre (elle est de 1/81 masse terrestre), la troisième loi de Kepler nous donne : 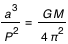où a est la distance Terre-Lune et P est la période de rotation anomalistique de la Lune autour de la Terre (P=27,55 jours correspondant au temps écoulé entre deux passages au périgée).

Calculer la masse de la Terre et la distance Terre-Lune par cette méthode.