Ex: Orbites perturbées du problème à 2 corps

Auteurs: Marc Fouchard, S. Renner, Stéphane Erard

Auteur: S. Renner

Orbites perturbées du problème à 2 corps

Difficulté : ☆ Temps : 1h

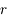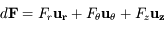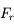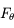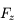Un corps en orbite elliptique autour du Soleil (de rayon vecteur ) est soumis à une force perturbatrice de la forme $d {\bf F} = F_r {\bf u_r} + F_\theta {\bf u_\theta} + F_z {\bf u_z}$ , où F_r , $F_\theta$ , F_z sont respectivement les composantes (constantes) radiale, tangentielle et normale de la force, et 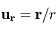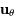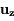${\bf u_r} = {\bf r}/r$ , ${\bf u_\theta}$ , ${\bf u_z}$ des vecteurs orthonormés unitaires. Cette force est suffisamment faible pour que la trajectoire de l'objet reste keplerienne.

Question 1)

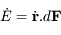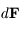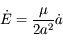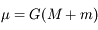On peut écrire la variation d'énergie ${\dot E}={\dot \bf r}.d{\bf F}$ due à la force $d {\bf F}$ . Sachant de plus que ${\dot E}= \frac{\mu}{2a^2} {\dot a}$ avec $\mu = G (M+m)$ , montrer quels types de forces vont modifier le demi-grand axe 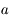en calculant da/dt .

Solution

Question 2)

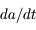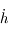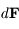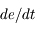En écrivant la variation du moment cinétique ${\dot h}$ due à $d {\bf F}$ , montrer quels types de forces modifient l'excentricité en calculant de/dt .

Solution