Ex : rétrogradation de Mars

Auteurs: Marc Fouchard, S. Renner, Stéphane Erard

Auteur: Marc Fouchard

Rétrogradation de Mars

Difficulté : ☆☆ Temps : 1h

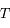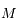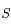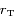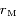On suppose que la Terre et Mars se déplacent uniformément sur des cercles centrés sur le Soleil . Soit $r_{\rm T}$ et $r_{\rm M}$ les rayons respectives des orbites de la Terre et de Mars, et 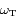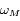$\omega_{\rm T}$ , $\omega_M$ leur vitesses angulaires respectives. On suppose que les plans de l'orbite de la Terre et de Mars sont confondus. 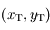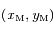Ainsi, dans un repère fixe centré sur le Soleil on note $(x_{\rm T},y_{\rm T})$ et $(x_{\rm M}, y_{\rm M})$ les coordonnées respectives de la Terre et de Mars. On suppose qu'initialement le Soleil, la Terre et Mars sont alignés dans cet ordre sur l'axe des abscisses du côté des abscisses positives.

Question 1)

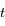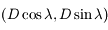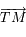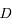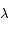Exprimer les coordonnées de la Terre et de Mars en fonction du rayon de leur orbite, de leur vitesse angulaire et du temps . Soit $(D\cos \lambda , D\sin \lambda)$ les coordonnées du vecteur $\overrightarrow{TM}$ . En déduire une expression de et de $\lambda$ en fonction de 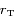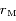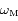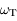$r_{\rm T}$ , $r_{\rm M}$ , $\omega_{\rm M}$ , $\omega_{\rm T}$ et .

Solution

Question 2)

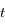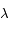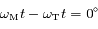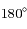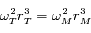Calculer la dérivée de $\lambda$ par rapport au temps, puis déterminer son signe pour $\omega_{\rm M}t-\omega_{\rm T}t=0^\circ$ et $180^\circ$ . On utilisera la propriété $\omega_T^2 r_T^3=\omega_M^2 r_M^3$ qui dérive de la troisième loi de Kepler. Conclure.

Solution

Question 3)

Cacluler la valeur de 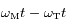$\omega_{\rm M}t-\omega_{\rm T}t$ lorsque 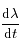$\frac{{\rm d} \lambda}{{\rm d} t}$ s'annule. Ces positions correspondent aux stations de Mars. On notera dans la suite 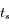t_s un instant conrrespondant à une station.

Solution

Question 4)

Calculer les deux instants correspondant aux stations en fonction de 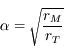$\alpha=\sqrt{\frac{r_M}{r_T}}$ . En déduire la durée de la rétrogradation.

Solution