Géométrie
- Introduction
- Théorème de Thalès
- Distance Terre Lune
- Ex: Distance Terre Lune
- Théorème de Pythagore
- Visibilité d'un satellite
- Ex: Visibilité d'un satellite
- Extinction atmosphérique
- Ex: Extinction atmosphérique
- Mesure de la vitesse de la lumière
- ex: Mesure de la vitesse de la lumière
- Applications
- La loi des aires
- Ex: La loi des aires
- Vitesse orbitale de la Terre
- Ex: Vitesse orbitale de la Terre
- Equation de Kepler
- Ex: Equation de Kepler
- Produits scalaire, vectoriel et mixte
- Dans le problème des 2-corps
- Ex : Dans le problème des 2-corps
- Les coniques
- Trajectoires balistiques dans le système solaire
- Ex: Trajectoire balistique dans le système solaire
- Les solutions du problème de deux corps
- Ex : les solutions du problème de deux corps
- Masse du trou noir central de la galaxie
- Ex: Masse du trou noir central de la galaxie
- Géométrie dans l'espace
- Angles solides
- Ex: angles solides
- Croissant de Lune
- Ex: Croissant de Lune
- En savoir plus: Croissant de Lune
Introduction
On trouvera dans cette partie les exercices suivants :
- Calcul de la distance Terre-Lune (application du théorème de Thalès)
- Visibilité d'un satellite artificiel (application du théorème de Pythagore)
- Extinction atmosphérique et observation du Soleil couchant (application des théorèmes de Pythagore et Al Kashi)
- Détermination historique de la vitesse de la lumière (application du théorème d'Al Kashi)
- Démonstration géométrique de la loi des aires
- Détermination de la vitesse orbitale de la Terre autour du Soleil (et de la distance Terre-Soleil) par l'effet Doppler-Fizeau
- Etablissement géométrique de l'équation de Képler
- Démonstration de la loi des aires et de l'intégrale de Laplace (application du produit vectoriel)
- Trajectoire balistiques dans le système solaire (application des coniques)
- Description des solutions du problème à deux corps (application des coniques)
- Estimation de la masse du trou noir central à partir de la trajectoire d'une étoile sur la sphère céleste (application des coniques)
- Angles solides et photométrie (géométrie dans l'espace)
- Croissant de Lune vu à l'horizontal (par la géométrie sphérique)
Théorème de Thalès
Auteur: Arnaud Beck
Distance Terre Lune
Auteur: Arnaud Beck
La première estimation de la distance Terre-Lune date de la Grèce antique. Pourtant elle est d'une précision remarquable. Elle a été effectuée par Aristarque de Samos vers 250 avant JC. Celui-ci a eu l'idée d'observer une éclipse de Lune pour comparer le rayon de la Lune avec l'ombre de la Terre projetée sur la Lune. Cette méthode est facile à mettre en oeuvre et d'une grande précision mais a l'inconvénient de donner uniquement le rapport des rayons lunaire et terrestre. Pour connaître la valeur du rayon de la Lune il faut donc connaître celui de la Terre.
Dans cet exercice, on se propose de refaire les calculs d'Aristarque de Samos en se basant sur les observations qu'il avait lui-même effectuées en son temps et de retrouver le rapport entre les rayons lunaire et terrestre.
Ex: Distance Terre Lune
Auteur: Arnaud Beck
 Calcul de la distance Terre-Lune
Calcul de la distance Terre-Lune
Difficulté : ☆
 Introduction
Introduction
Eclipse de soleil
Il est connu que pendant une éclipse de Soleil, la Lune vient se placer entre la Terre et le Soleil et cache presque exactement le Soleil aux observateurs terrestres. Cela est possible car depuis la Terre, la Lune et le Soleil ont le même rayon apparent. Soit 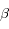 le demi-angle sous lequel ces deux astres sont vus depuis la Terre (voir partie droite de la figure ci-dessous). Cet angle est connu directement par l'observation et vaut à peu près 0,25°.
le demi-angle sous lequel ces deux astres sont vus depuis la Terre (voir partie droite de la figure ci-dessous). Cet angle est connu directement par l'observation et vaut à peu près 0,25°.
Eclipse de Lune
Une éclipse de Lune se produit lorsque la Lune passe dans le cône d'ombre de la Terre éclairée par le Soleil (voir partie gauche de la figure ci-dessous). Soit 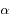 l'angle d'ouverture de ce cône. Sa valeur est a priori inconnue. Aristarque de Samos avait observé que la largeur de ce cône au niveau de la Lune était de 3 diamètres lunaires.
l'angle d'ouverture de ce cône. Sa valeur est a priori inconnue. Aristarque de Samos avait observé que la largeur de ce cône au niveau de la Lune était de 3 diamètres lunaires.
Pour une question de lisibilité de la figure, la Lune n'a pas la même échelle sur la partie droite que sur la partie gauche. Les deux phénomène étant indépendants, cela n'a pas d'incidence sur le raisonnement.
Eclipses de soleil et de lune

La partie droite de la figure représente la configuration d'une éclipse de soleil et la partie gauche la configuration d'une éclipse de Lune.
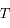
,
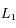
,
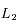
et
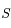
sont respectivement les positions de la Terre, de la Lune pendant une éclipse de soleil, de la Lune pendant une éclipse de Lune, et du Soleil.
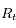
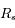
et
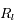
sont les rayons terrestre, solaire et lunaire.
Crédit :
Arnaud Beck
Question 2)
Que dire de 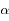 et
et 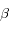 si on suppose le Soleil très grand devant la Terre ?
si on suppose le Soleil très grand devant la Terre ?
Il s'agit de trouver un équivalent de 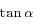 quand
quand 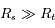
Question 3)
Avec l'hypothèse précédente, calculer la valeur de 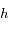 (défini sur la figure).
(défini sur la figure).
Théorème de Pythagore
Auteur: Arnaud Beck, Stéphane Erard, Alain Vienne
Visibilité d'un satellite
Auteur: Alain Vienne
On propose ici une application simple et directe du thèorème de Pythagore. Il faut le considérer ici comme une révision
des "années collège et lycée" de l'étudiant. Notre expérience d'enseignement montre que cela n'est pas inutile.
On considère un satellite à une certaine altitude. Il s'agit de savoir sur quelle partie de la Terre
il sera visible. Cet excercice peut s'appliquer directement pour savoir d'où est visible une
montagne.
L'exercice proposé dans la partie "intégrale de Rieman" est plus complet et calcule notamment la surface correspondante.
Ex: Visibilité d'un satellite
Auteur: Alain Vienne
 Zone visible d'une montagne ou d'un satellite
Zone visible d'une montagne ou d'un satellite
Difficulté : ☆
Temps : 20 mn
Question 1)
Soit un satellite artificiel de hauteur 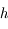 , sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
, sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
Question 2)
Le rayon de la Terre étant de 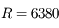 km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
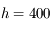 km?
km?
Extinction atmosphérique
Auteurs: Arnaud Beck, Stéphane Erard
Quand le Soleil est au zénith, impossible de le regarder à l'oeil nu sans être ébloui voire même se brûler la rétine. Pourtant, le soir tombé, on peut admirer le Soleil couchant sans la moindre gêne.
Cela s'explique simplement par la diffusion des rayons solaires par les molécules de l'atmosphère. En effet, quand les rayons du Soleil rencontrent une molécule, une partie d'entre eux est déviée ou absorbée. Et plus le nombre de particules qu'ils rencontrent est grand, plus la proportion de rayons déviés est grande et l'énergie lumineuse reçue par l'observateur sera réduite d'autant.
Dans cet exercice, on propose de quantifier le nombre de particules rencontrées par un rayon de Soleil en fonction de sa position dans le ciel par rapport à un observateur potentiel.
Le parcours atmosphérique est également calculé dans le cas général.
Ex: Extinction atmosphérique
Auteur: Arnaud Beck, Stéphane Erard
 Pourquoi peut-on regarder le Soleil couchant ?
Pourquoi peut-on regarder le Soleil couchant ?
Difficulté : ☆
Temps : 1h
Le nombre de particules atmosphériques rencontrées par un rayon de Soleil le long de son parcours est appelé densité de colonne, et est égal à :
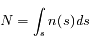
où 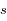 est la coordonnée le long du trajet du rayon et
est la coordonnée le long du trajet du rayon et 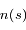 est la densité atmosphérique au point de coordonnée
est la densité atmosphérique au point de coordonnée 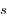 .
.
On peut approximer la densité atmosphérique à faible altitude (là où elle est la plus dense) par:
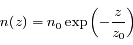
où 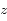 est l'altitude (mesurée verticalement),
est l'altitude (mesurée verticalement), 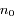 est la densité au niveau du sol, et
est la densité au niveau du sol, et 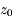 est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la loi barométrique.
est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la loi barométrique.
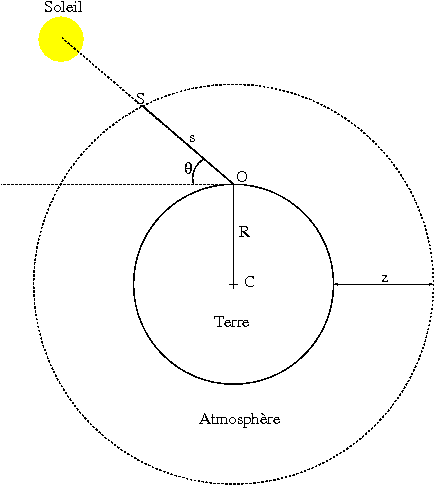
La figure ci-dessous représente la situation. Le centre de la Terre est au point C, l'observateur en O. Le point S représente le point de coordonnée 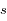 sur le trajet du rayon de Soleil, et d'altitude
sur le trajet du rayon de Soleil, et d'altitude 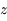 .
. 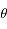 est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
Arrivée d'un rayon de Soleil sur Terre
Question 1)
Dans le cas du Soleil couchant (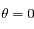 ), donner l'expression de l'altitude
), donner l'expression de l'altitude 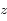 en fonction de la coordonnée
en fonction de la coordonnée 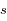 .
.
Question 3)
Reprendre les questions 1) et 2) pour donner l'expression de 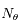 , la densité de colonne pour une position
, la densité de colonne pour une position 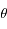 quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc
quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc 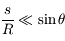 .
.
Dans ce cas, on utilise le théorème de Pythagore généralisé (ou loi des cosinus)
Auteur: Stéphane Erard
 Calcul de la masse d'air
Calcul de la masse d'air
Difficulté : ☆
Temps : 30 min
Le rapport  de l'exercice précédent est appelé masse d'air en Astronomie. C'est le chemin optique parcouru dans l'atmosphère par rapport à la position zénitale. Suffisamment loin de l'horizon, on a en bonne approximation
de l'exercice précédent est appelé masse d'air en Astronomie. C'est le chemin optique parcouru dans l'atmosphère par rapport à la position zénitale. Suffisamment loin de l'horizon, on a en bonne approximation 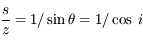 , où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'approximation plan-paralléle. On cherche toujours à observer les astres sous faible masse d'air (< 2) pour limiter l'extinction atmosphérique.
, où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'approximation plan-paralléle. On cherche toujours à observer les astres sous faible masse d'air (< 2) pour limiter l'extinction atmosphérique.
On veut maintenant calculer exactement la longueur du chemin optique parcouru par les rayons lumineux dans l'atmosphère pour étudier la validité de l'approximation précédente.
Question 1)
Reprendre la question 3 de l'exercice précédent : dériver une relation entre l'altitude 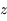 et la coordonnée
et la coordonnée 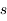 pour une hauteur
pour une hauteur 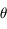 quelconque.
quelconque.
On exprimera cette relation en fonction de l'angle zénital  (compté à partir de la verticale locale).
(compté à partir de la verticale locale).
Question 2)
Résoudre en 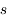 .
.
Question 3)
Tracer 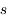 en fonction de l'angle zénital
en fonction de l'angle zénital  et comparer avec l'approximation usuelle en sécante (
et comparer avec l'approximation usuelle en sécante (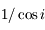 ).
).
Question 4)
Quel est le domaine de validité de l'approximation en sécante ?
Quels autres phénomènes affectent la diffusion dans ces conditions ? Conclusion ?
Mesure de la vitesse de la lumière
Auteur: Stéphane Erard
Depuis l'antiquité jusqu'au XVIIe siècle, plusieurs conceptions de la lumière se sont succédées. Il était notamment impossible de dire si la lumière se propage instantanément ou à vitesse finie. En 1676, Ole Römer met en évidence une vitesse de propagation finie, dont il estime un ordre de grandeur correct à partir de l'observation des satellites de Jupiter. Cette méthode est reproduite ici.
ex: Mesure de la vitesse de la lumière
Auteur: Stéphane Erard
 Mouvement des satellites de Jupiter
Mouvement des satellites de Jupiter
Difficulté : ☆
Temps : 60 min
En 1668, Gian Domenico Cassini a publié les premières éphémérides des satellites galiléens. L'intérêt de ces phénomènes était de fournir une horloge visible et consultable partout sur Terre : les débuts d'éclipse des satellites. Ceux-ci permettent de déterminer la longitude du lieu d'observation par comparaison avec une horloge locale.
Dans les années suivantes, Römer mit néanmoins en évidence des écarts importants avec ses propres observations de Io, le plus proche satellite de Jupiter, et le plus rapide. Ces écarts augmentaient (jusqu'à 11 minutes) puis diminuaient avec une périodicité d'un an.
Question 1)
On considère la situation de la Figure 1, lorsque Io est en émersion au point D (il sort de l'ombre de Jupiter). Durant un premier événement la Terre est au point L de son orbite, lors du suivant elle est en K.
Si la lumière se propage instantanément, quel intervalle sépare les deux événements ?
Question 2)
Même question en supposant que la lumière se déplace à la vitesse c. Remarques sur la Figure 1 ? Préciser les approximations implicites qu'on a fait.
Question 3)
Calculer en unités astronomiques la distance Terre-Jupiter à l'opposition (lorsque les deux planètes sont au plus près).
Question 4)
On effectue une première observation d'éclipse à l'opposition. A quel moment peut-on effectuer une seconde observation pour laquelle le décalage sera maximum ?
Question 5)
On observe 261 jours après l'opposition. De quels angles se sont déplacés Jupiter et la Terre sur leurs orbites depuis l'opposition ? Quel est l'angle Jupiter-Soleil-Terre à ce moment ?
On donne la période sidérale de Jupiter, 4335,35 jours, bien connue à l'époque.
Question 6)
Calculer la distance Terre-Jupiter  en unités astronomiques au moment de la deuxième observation.
en unités astronomiques au moment de la deuxième observation.
La distance Soleil-Jupiter est de 5,2 unités astronomiques.
Question 7)
Le second événement est observé avec 13,5 min de retard par rapport à un phénomène régulier. En déduire une estimation de la vitesse de la lumière.
Applications
Auteurs: Alain Vienne, S. Renner
La loi des aires
Auteur: Alain Vienne
La loi des aires dit que, dans le problème de l'interaction gravitationnelle de deux corps, l'aire balayée par le rayon vecteur est proportionnel au temps. Cette loi est aussi appelée "deuxième loi de Kepler" (voir aussi dans ce même chapitre, le lien suivant).
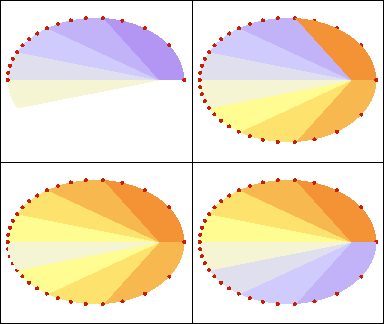
La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
En fait, la loi des aires est plus générale que la deuxième loi de Kepler puisque qu'elle s'applique pour toute force centrale. Pour la démontrer, il faut bien-sur utiliser la loi fondamentale de la dynamique:
Principe fondamental de la dynamique
L'accélération d'un mobile est proportionnelle à la force à laquelle il est soumis.
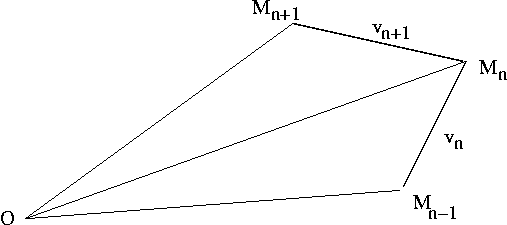
La preuve qui est proposée en exercice utilise un modèle discret. Elle est directement inspirée d'une application isssue du livre de Daniel Perrin "Nombre, mesures et géométrie" (Ed. CASSINI). Ainsi le temps est une juxtaposition d'instants 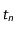 de durée très courte
de durée très courte 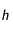 de telle sorte que
de telle sorte que 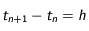 . La discrétisation revient à supposer qu'entre les instants
. La discrétisation revient à supposer qu'entre les instants 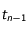 et
et 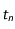 , le mobile se déplace de
, le mobile se déplace de 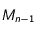 à
à 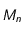 avec la vistesse constante
avec la vistesse constante 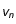 . En vecteur la vistesse est donc
. En vecteur la vistesse est donc 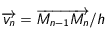 . Sur l'intervalle suivant
. Sur l'intervalle suivant ![[t_n,t_{n+1}]](../pages_applications/equations_applications/equation10.png) , la vitesse est différente mais constante aussi pour cette durée:
, la vitesse est différente mais constante aussi pour cette durée: 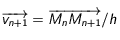 . Ainsi à l'instant
. Ainsi à l'instant 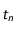 l'accélération est
l'accélération est 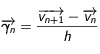 .
.
Le modèle continu s'obtient facilement par passage à la limite.
La loi fondamentale de la dynamique s'écrit alors: 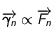
Les outils mathématiques nécéssaires à cette preuve se limitent alors à deux petits lemmes que Daniel Perrin nomment lemmes de découpage et que nous admettrons:
Ex: La loi des aires
Auteur: Alain Vienne
 La loi des aires
La loi des aires
Difficulté : ☆☆
Temps : 1h
Question 1)
Montrer qu'à tout instant (c'est-à-dire pour tout entier 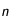 ), on a:
), on a: 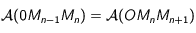
Cela signifie bien que l'aire balayé par le rayon vecteur 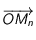 est proportionnel au temps parcouru.
est proportionnel au temps parcouru.
Lemme de la médiane dans le triangle 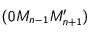 pour avoir
pour avoir 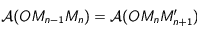
Vitesse orbitale de la Terre
Auteur: S. Renner
Date de création: 2 mars 2009
 Introduction
Introduction
L'effet Doppler-Fizeau représente le décalage en fréquence d'une onde lumineuse entre les mesures à l'émission et à la réception, lorsque la distance entre un émetteur et un récepteur varie au cours du temps.
Par exemple, lors du passage d'un camion de pompier muni d'une sirène, c'est l'effet Doppler qui se manifeste dans la perception de la hauteur du son (plus aigu lorsque le véhicule se rapproche, plus grave lorsqu'il s'éloigne).
Ce phénomène est particulièrement important en astronomie car il permet de mesurer les vitesses (d'approche ou d'éloignement) des objets célestes.
On observe Arcturus, troisième étoile la plus brillante du ciel (dans la constellation du Bouvier), à deux dates 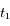 et
et 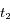 espacées de 6 mois.
espacées de 6 mois.
La latitude par rapport au plan de l'orbite de la Terre est 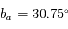 , et la longitude par rapport à une direction fixe
, et la longitude par rapport à une direction fixe 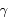 est
est 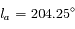 . A l'instant
. A l'instant 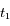 la longitude de la Terre est
la longitude de la Terre est 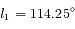 , et
, et 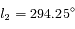 à l'instant
à l'instant 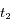 . Voir la figure ci-dessous pour les conditions d'observation.
. Voir la figure ci-dessous pour les conditions d'observation.
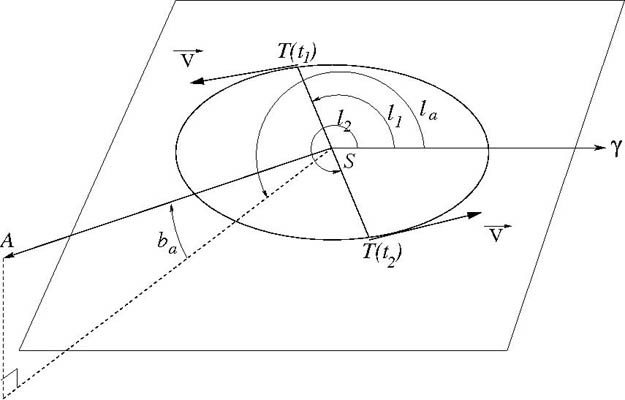
Situation de l'observation d'Arcturus. Voir texte pour la valeur des angles.
On effectue aux dates 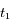 et
et 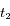 un spectre de la lumière de l'étoile. L'étude des raies d'absorption permet de remarquer qu'une raie d'absorption du fer, qui normalement se situe à
un spectre de la lumière de l'étoile. L'étude des raies d'absorption permet de remarquer qu'une raie d'absorption du fer, qui normalement se situe à 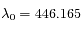 nm, est mesurée
nm, est mesurée 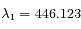 nm sur le spectre obtenu à la date
nm sur le spectre obtenu à la date 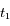 , et
, et 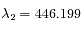 nm sur celui obtenu à la date
nm sur celui obtenu à la date 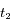 .
.
L'objectif est d'en déduire la vitesse orbitale de la Terre autour du Soleil, ainsi que la distance moyenne Terre-Soleil.
Ex: Vitesse orbitale de la Terre
Auteur: S. Renner
 Vitesse orbitale de la Terre
Vitesse orbitale de la Terre
Difficulté : ☆
Temps : 1h30
On fait l'hypothèse que l'orbite de la Terre est circulaire est que celle-ci est décrite avec une vitesse uniforme 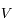 .
.
Question 4)
Calculer la distance Terre-Soleil en km sachant que la période de révolution est 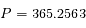 jours.
jours.
Equation de Kepler
Auteur: S. Renner
Date de création: 16 mai 2013
On reprend les résultats obtenus dans l'exercice sur la résolution du problème des 2 corps. Le but ici est d'établir l'équation de Kepler à l'aide de la géométrie essentiellement, plutôt que par le calcul.
L'équation de Kepler (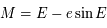 ) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne
) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne 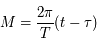 , avec
, avec 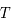 la période orbitale,
la période orbitale,  le temps et
le temps et 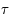 l'instant de passage au péricentre.
l'instant de passage au péricentre.
Les trois anomalies
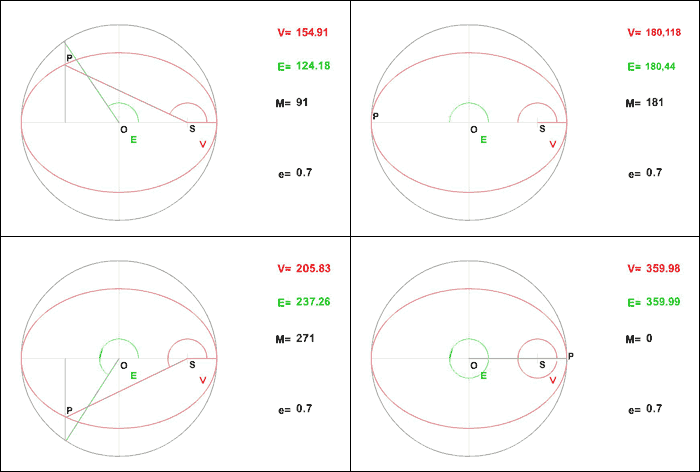
Ex: Equation de Kepler
Auteur: S. Renner
 Equation de Kepler
Equation de Kepler
Difficulté : ☆
Temps : 1h
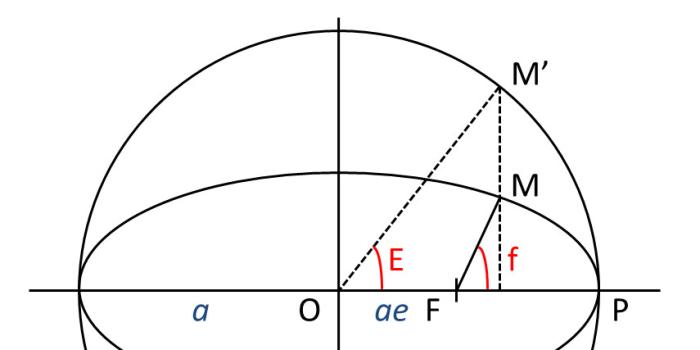
Trajectoire elliptique d'un corps
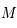
(de foyer
, péricentre
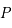
, demi-grand axe
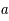
, excentricité
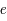
), cercle principal, anomalie excentrique
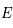
et vraie
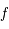
Question 2)
Calculer l'aire délimitée par les points 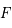 ,
, 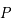 ,
, 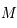 .
.
Question 3)
En déduire l'équation de Kepler 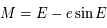 .
.
Produits scalaire, vectoriel et mixte
Auteur: Alain Vienne
Dans le problème des 2-corps
Auteur: Alain Vienne
Quand on formule le problème des 2-corps, on arrive au problème de Képler, c'est-à-dire à l'équation différentielle vectorielle suivante:
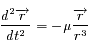
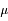 est une constante réelle positive et
est une constante réelle positive et 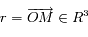 .
. 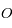 est un point fixe et on étudie le mouvement de
est un point fixe et on étudie le mouvement de 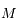 .
.
Les deux exercices proposés donnent la loi des aires et l'intégrale de Laplace.
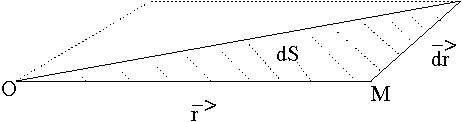
En fait, le premier exercice aura 2 conséquences: la première est que le mouvement est plan et la deuxième que la loi du mouvement est la loi des aires proprement dite:
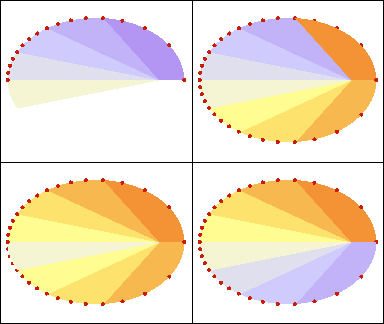
La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
Ex : Dans le problème des 2-corps
Auteur: Alain Vienne
 La loi des aires
La loi des aires
Difficulté : ☆
Temps : 20mn
 Introduction
Introduction
La loi des aires est très facile à obtenir avec le produit vectoriel. Sans le produit vectoriel, on peut aller voir cet exercice.
Question 1)
Montrer que dans le problème képlérien, le moment cinétique:
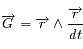
est invariant.
Dériver 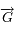 et utiliser que
et utiliser que 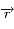 et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
Question 2)
Montrer que le mouvement de 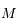 se fait dans un plan passant par le point
se fait dans un plan passant par le point 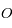 et orthogonal à
et orthogonal à 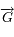 .
.
Question 3)
En utilisant un élément d'aire 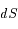 parcouru par
parcouru par 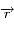 pendant l'élément de temps
pendant l'élément de temps 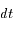 , montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
, montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
L'aire 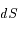 est la moitié du parallélogramme suivant:
est la moitié du parallélogramme suivant:
Auteur: Alain Vienne
 Intégrale de Laplace
Intégrale de Laplace
Difficulté : ☆
Temps : 20mn
Question 1)
Montrer l'expression suivante:
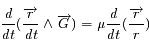
Partir du premier membre de l'expression et utiliser le problème de képler et l'invariance du moment cinétique.
Remarquer que 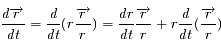
Utiliser que 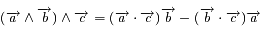
La norme de 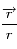 est constante donc
est constante donc 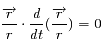
Question 2)
Déduire de l'égalité précédente une expression qui est constante pendant le mouvement (intégrale de Laplace).
Les coniques
Auteurs: Marc Fouchard, Alain Vienne
Trajectoires balistiques dans le système solaire
Ex: Trajectoire balistique dans le système solaire
Auteur: Alain Vienne
 Trajectoire balistique dans le système solaire
Trajectoire balistique dans le système solaire
Difficulté : ☆☆
Temps : 1h30
Question 1)
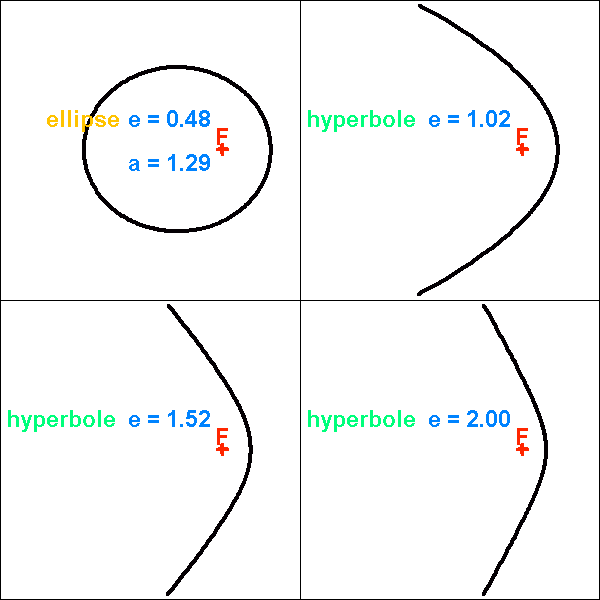
Une conique est défine par 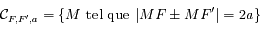 . Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
. Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
Question 4)
Montrer qu'aucune trajectoire physique n'est possible quand 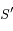 se trouve entre
se trouve entre 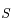 et
et 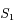 .
.
Les solutions du problème de deux corps
Ex : les solutions du problème de deux corps
Auteur: Marc Fouchard
 Les solutions du problème de deux corps
Les solutions du problème de deux corps
Difficulté : ☆
Temps : 1 h
Question 1)
Montrer que si 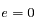 la solution est un cercle dont on déterminera le rayon.
la solution est un cercle dont on déterminera le rayon.
Question 4)
Montrer que si 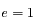 on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
Question 5)
Montrer que si 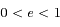 on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
Question 6)
Montrer que si 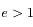 on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.
on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.
Masse du trou noir central de la galaxie
Auteur : Alain Vienne
On dispose d'un tracé de l'orbite apparente d'une étoile (appelée S2) autour d'un point (SgrA) localisé par diverses méthodes comme étant au centre de notre Galaxie. Cette orbite est une ellipse qui diffère de l'orbite réelle car elle est vue en projection sur la sphère céleste. Le plan de la figure ci-dessous est le plan perpendiculaire à la ligne de visée: le plan de projection On se propose de trouver les caractéristiques géométriques de l'ellipse réelle, qui permettent finalement de calculer la masse centrale: sa valeur n'est compatible qu'avec celle d'un trou noir. On utilise la troisième loi de képler qui relie cette masse, la période et le demi-grand axe.
Orbite apparente d'une étoile autour de SgrA
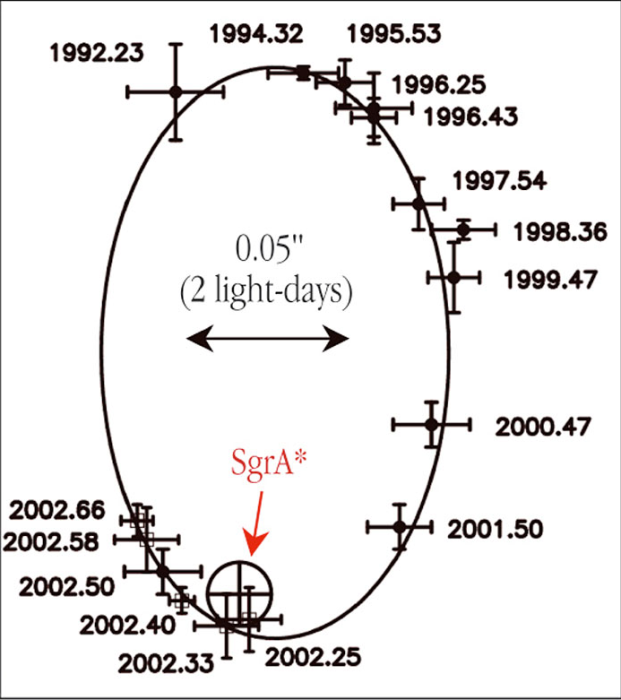
Crédit :
European Southern Observatory / ESO
Ex: Masse du trou noir central de la galaxie
Auteur: Alain Vienne
 Masse du trou noir central de la galaxie
Masse du trou noir central de la galaxie
Difficulté : ☆☆
Temps : 1h30
Question 1)
Localiser le centre 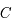 de l'ellipse projetée
de l'ellipse projetée
Question 2)
Tracer le grand axe projeté 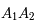
Question 4)
Tracer le diamètre conjugué 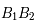 de
de 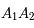 (donc le projeté du petit axe).
(donc le projeté du petit axe).
Question 5)
Tracer point par point le projeté du cercle principal, par l'homothétie de l'ellipse projetée à 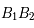 et de rapport
et de rapport 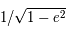 .
.
La définition du cercle principal est donc:
Cercle principal d'une ellipse: Cercle de rayon a (demi grand axe de l'ellipse) de centre C
Question 7)
Estimer la période du mouvement en utilisant les dates d'observations indiquées sur le tracé.
Question 8)
En déduire la masse 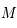 présente au foyer SgrA.
présente au foyer SgrA.
Pour utiliser les unités ua et l'année, utiliser 2 fois la troisième de Kepler: une fois pour le système Soleil-Terre et une fois pour le système S2-SgrA.
Géométrie dans l'espace
Auteurs: Stéphane Erard, Alain Vienne
Angles solides
On cherche à caractériser la partie de l'espace délimitée par un cône de sommet O et de demi-ouverture 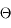 . On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
. On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
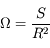
est indépendante de R. Elle mesure l'angle solide défini par le cône.
Cette quantité sans dimension est mesurée en stéradians (sr) - voir la définition des unités physiques.
Ex: angles solides
 Angles solides
Angles solides
Difficulté : ☆
Temps : 30 min
Question 1)
Quel est l'angle solide sous-tendu par un demi-espace ? Par l'espace complet ?
Question 2)
Quel est l'angle solide sous-tendu par une surface quelconque, de quoi dépend-il ?
Ecrire l'application à une surface plane élémentaire dS inclinée sur la ligne de visée.
Question 3)
Donner l'expression différentielle de l'angle solide élémentaire en coordonnées sphériques.

Crédit :
Sharayanan/GNU Free Documentation License
Question 4)
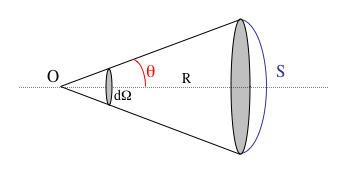
On considère maintenant une couronne circulaire élémentaire de demi-ouverture 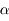 . Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture
. Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture 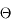 .
.
Question 5)
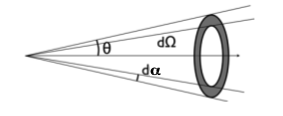
Que devient cette valeur si l'angle 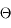 est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
 Photométrie
Photométrie
Difficulté : ☆☆
Temps : 30 min
Question 1)
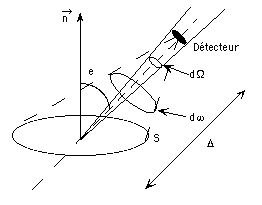
On observe une surface plane à l'aide d'une caméra, dans la configuration de la figure ci-dessous : le détecteur de la caméra a une surface 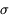 , on observe la source de surface S sous un angle e à la distance
, on observe la source de surface S sous un angle e à la distance  . Les dimensions sont telles que les angles solides considérés sont petits (
. Les dimensions sont telles que les angles solides considérés sont petits (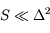 ).
).
Ecrire l'angle solide sous lequel le détecteur voit la source. Ecrire l'angle solide sous lequel la source voit la surface collectrice. Dériver une relation entre les deux angles solides.
Question 2)
On note W' la puissance lumineuse diffusée par la source par unité d'angle solide. L'éclairement (ou irradiance) est la puissance recueillie par unité de surface de détecteur en provenance de la source.
Ecrire l'éclairement E en fonction de la puissance totale reçue par le détecteur (dW). Quelle est l'unité de mesure de cette quantité dans le Système International ? De quoi dépend-elle en général ?
Question 3)
La luminance (ou intensité spécifique) d'une source est la puissance lumineuse émise ou diffusée dans un angle solide élémentaire par unité de surface apparente.
Ecrire la luminance en fonction de dW. Dans quelle unité SI se mesure cette quantité ? De quoi dépend-elle en général ?
Question 4)
Ecrire l'éclairement reçu par le détecteur en fonction de la luminance de la source et de la distance. Que signifie cette expression si la source est ponctuelle (c'est-à-dire si elle ne remplit pas le champ de l'instrument) et dans le cas contraire ?
 Intégrales angulaires
Intégrales angulaires
On trouvera ici des exercices d'intégration angulaire sur les quantités photométriques.
Croissant de Lune
Auteur: Alain Vienne (et le groupe IREM de Lille1)
On se propose d'établir les conditions pour que le croissant de Lune soit vu d'un lieu de la Terre comme une gondole:
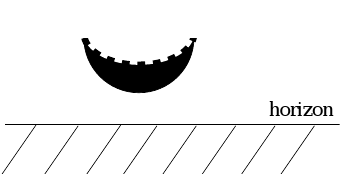
Croissant de Lune vu horizontalement (comme une "gondole").
Nous allons étudier ce problème par la trigonométrie sphérique qui permet de voir facilement les choses. La notion de sphère céleste est issue du fait que, à un lieu donné et à une date donnée, l'observateur n'a pas accès à la distance entre lui et l'objet céleste. Cet observateur peut alors considérer que tous ces objets sont à une même distance (arbitraire). Cela revient à dire que l'observateur n'appréhende que les directions issues de sa position. Or l'ensemble de ces directions s'identifie à une sphère centrée sur ce point.
Aucune formule n'est nécessaire pour résoudre l'exercice suivant. Il suffit de connaitre les bases. Soit:
- On considère une sphère de rayon 1.
- L'intersection de tout plan passant son centre avec la sphère est un grand cercle. Les grands cercles sont les géodésiques de la sphère.
- On s'oriente sur la sphère par la donnée un grand cercle orienté (ou de manière équivalente par un point appelé pôle qui est situé à 90° du grand cercle origine) et par une origine sur ce grand cercle.
Ex: Croissant de Lune
Auteur: Alain Vienne
 Exercice
Exercice
Difficulté : ☆☆
Temps : 2h
Question 1)
Montrer que la condition d'horizontalité du croissant de Lune nécessite que la Lune et le Soleil aient le même azimut.
Question 2)
La condition de même azimut est donc une condition nécessaire. Réciproquement, si cette condition est réalisée, préciser les conditions sur les hauteurs du Soleil et de la Lune pour que le croissant soit vu comme une "gondole" et non à l'envers (un "D" renversé).
La hauteur est l'angle sur le vertical (cercle de même azimut). Il est compté de -90° à 90° par rapport à l'horizon.
Question 3)
Cette figure donne, pour chaque position
de la Lune sur le même vertical que le Soleil (quand la condition
est réalisée), l'aspect de celle-ci.
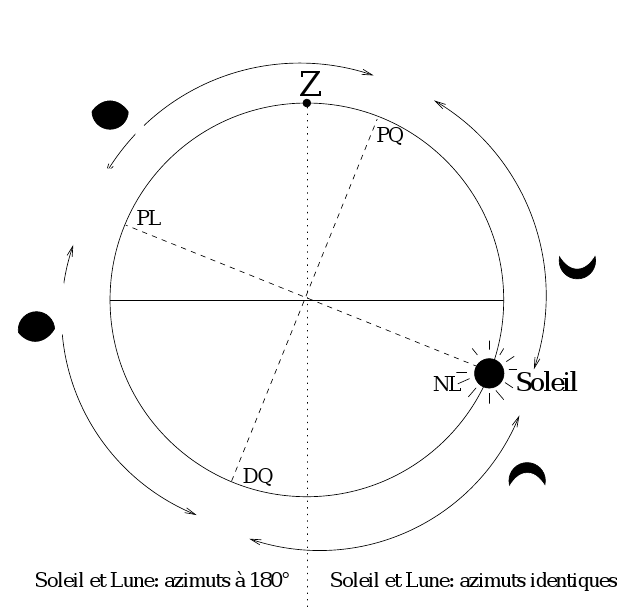
Phases de la Lune sous la condition de
même azimut. Figure dans le vertical de la Lune (et du Soleil).
La position du zénith sur le cercle est indicatif. Elle correspond
au cas de la figure donnée en solution de la question précédente. Bien-sur, si le zénith
est ailleurs sur le cercle, cela change les conditions de lever/coucher
du Soleil et de la Lune. Faites d'autres figures en changeant le zénith de place (cela déplace aussi l'horizon).
Question 4)
En supposant que la Lune est toujours sur l'écliptique, donner les seuls endroits de la Terre où il est possible de voir le croissant de Lune horizontal.
Aucun calcul n'est nécessaire pour répondre à cette question. Une discussion avec les proprietés élémentaires de la géométrie sphérique devrait suffire.
En savoir plus: Croissant de Lune
Auteur: Alain Vienne (et le groupe IREM de Lille1)
Il est peut-être plus facile de voir les 2 cas (coplanaire et non-coplanaire)
en raisonnant sur la sphère des fixes. Précédemment,
on regardait le mouvement diurne d'un point de la sphère des fixes
(le pôle 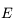 de l'écliptique) sur la sphère locale (de pôle
de l'écliptique) sur la sphère locale (de pôle 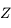 ).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de
).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de 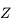 sur la sphère des fixes. On utilise la
condition suivante:
sur la sphère des fixes. On utilise la
condition suivante:
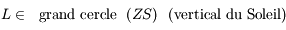
En effet, nous avons vu que c'est la condition pour voir la Lune comme
une gondole (ou tout au moins, la Lune à l'horizontal).
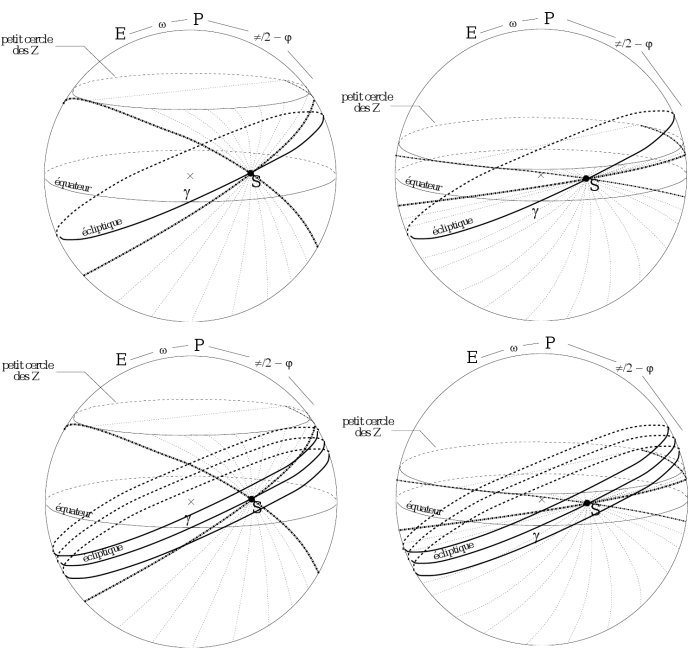
Petit cercle des zéniths sur la
sphère des fixes durant le mouvement diurne. Cas d'une zone tempérée
(à gauche) et d'une zone intertropicale (à droite). Cas de la Lune
sur l'écliptique (en haut) et cas de la Lune de part et d'autre de
l'écliptique à
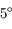
au plus (en bas).
Crédit :
Alain Vienne / IREM de Lille
Sur une sphère des fixes où on a placé l'équateur, l'écliptique et
leur pôle, et pour une latitude 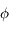 donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des
donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des 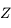 ). A chacune de
ces positions de
). A chacune de
ces positions de 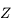 , il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des
, il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des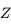 . En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des
. En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des 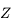 est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
La Lune doit se trouver dans la première partie (les "faisceaux" de la figure).
La frontière entre ces deux parties correspond au vertical du Soleil
qui est tangent au petit cercle des 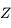 .
.
Cas de la Lune sur l'écliptique: Ce cas correspond aux 2 dessins du haut de la figure.
En dehors de la zone intertropicale (à gauche), l'écliptique coupe
les "faisceaux" qu'en ses sommets: au Soleil et au point
diamétralement opposé. Si on impose à la Lune d'être sur l'écliptique,
il n'y a qu'en ces points que la condition est réalisée (éclipses).
Par contre, dans la zone intertropicale, tout l'écliptique est contenu
dans les "faisceaux". Ainsi la condition est réalisée deux
fois par jour comme on l'a vu dans précédemment.
Cas où la Lune est de part et d'autre de l'écliptique:
L'orbite de la Lune est inclinée d'environ 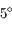 sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de
sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de 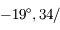 an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de
an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de 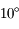 . Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
. Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
On remarque ainsi qu'au voisinage de la pleine Lune ou au voisinage
de la nouvelle Lune, la condition de "Lune horizontale"
est possible partout sur la Terre.
Mais on se rend bien compte que, loin des tropiques, la zone est étroite. Elle s'agrandit
au fur et à mesure que le lieu considéré s'approche du tropique.
Dans le cas d'un lieu dans la zone intertropicale, la possibilité
d'une telle condition est grande. La probabilité de réalisation l'est
donc aussi. Cependant cette probabilité n'est pas 1, car on voit
apparaitre une petite zone de la bande lunaire qui croise la partie
où il n'y a pas de vertical du Soleil (en dehors des "faisceaux").
Cette zone est petite et proche du Soleil. Ainsi même dans la zone
intertropicale, il peut y avoir des jours où la Lune n'est pas vue
à l'horizontal. Cela se produit pour des positions particulières de
l'orbite lunaire et pour des dates proches de la pleine Lune ou de
la nouvelle Lune.
Réponses aux exercices
pages_thales/exo-terre-lune.html
Exercice
'Calcul de la distance Terre-Lune'
pages_pythagore/exo-visibilite-satellite.html
Exercice
'Zone visible d'une montagne ou d'un satellite'
pages_pythagore/exo-pythagore.html
Exercice
'Pourquoi peut-on regarder le Soleil couchant ?'
-
Question 1
Solution :
Dans le triangle rectangle COS, le théorème de Pythagore donne:
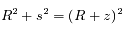
soit
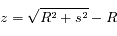
-
Question 2
Aide :
Aide au calcul :
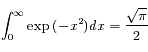
Cette intégrale est une des intégrales gaussiennes calculées ailleurs.
Solution :
On peut développer l'expression précédente de 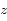 au premier ordre :
au premier ordre :
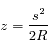
La densité de colonne vaut alors :
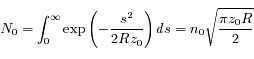
-
Question 3
Aide :
Dans ce cas, on utilise le théorème de Pythagore généralisé (ou loi des cosinus)
Solution :
La loi des cosinus donne :
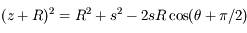
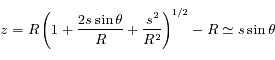
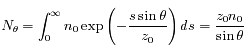
-
Question 4
Solution :
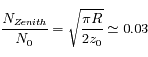
Quand le Soleil est au zénith, les rayons ne rencontrent que 3% des molécules qu'ils rencontrent lorsque le Soleil est sur le point de se coucher, et la différence de diffusion est en proportion. Cela explique l'énorme différence d'énergie lumineuse perçue, et qu'on puisse regarder le Soleil couchant à l'œil nu.
pages_pythagore/exo-pythagore.html
Exercice
'Calcul de la masse d'air'
-
Question 1
Solution :
On a comme précédemment :
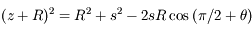
Soit
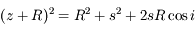
-
Question 2
Solution :
On a une équation de second degré :
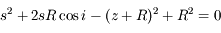
dont le discriminant est :
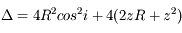
et les solutions :
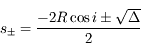
Seule la solution positive représente une distance :
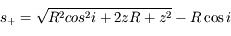
-
Question 3
Solution :
Masse d'air
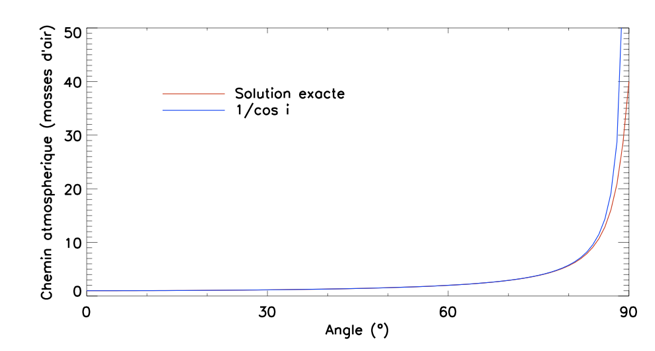
L'approximation en sécante diverge près de l'horizon, où elle ne représente plus une solution physique.
Pour convertir les masses d'air en densité de colonne, il faut fixer une valeur pour la masse d'air 1. On prend naturellement l'échelle de hauteur fournie par la loi barométrique, ou dérivée d'une mesure de pression locale.
-
Question 4
Solution :
On voit que l'approximation par la sécante est très bonne jusqu'à des distances zénitales au-delà de 80° — les télescopes professionnels refusent de pointer si bas sur l'horizon.
Avec l'augmentation de la masse d'air, les rayons lumineux sont non seulement atténués, mais également déviés - on peut voir dans certaines conditions des objets situés sous l'horizon géométrique. L'intérêt de l'expression dérivée ci-dessus est donc limité, la correction optique de réfraction étant en pratique plus importante.
pages_pythagore/exo-vitesse-lumiere.html
Exercice
'Mouvement des satellites de Jupiter'
-
Question 1
Solution :
Si la lumière se propage instantanément les événements sont observés à intervalles réguliers, qui ne dépendent que du mouvement de Io. Cet intervalle est simplement la période de révolution de Io autour de Jupiter (T ~ 42h 28 min).
-
Question 2
Solution :
Si la lumière se propage à vitesse finie, le premier événement est observé avec un décalage 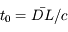 , le second avec
, le second avec 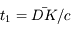 . L'intervalle entre les observations est donc
. L'intervalle entre les observations est donc 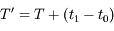 . Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et
. Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et 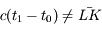 .
.
On a considéré implicitement que tous les mouvements de révolution s'effectuent dans le même plan, ce qui n'est pas tout à fait vrai. Cette hypothèse conditionnera la précision du résultat sur l'estimation de c.
-
Question 3
Solution :
On appelle 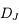 la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors
la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors 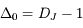 ua.
ua.
-
Question 4
Solution :
Lors de la conjonction (lorsque les deux planètes sont éloignées au maximum) l'observation est impossible : le Soleil s'interpose devant Jupiter. La seconde observation s'effectue donc soit avant soit après la conjonction, lorsque l'écart angulaire entre Jupiter et le Soleil est suffisamment grand pour observer de nouveau les satellites (typiquement ~ 20°).
-
Question 5
Aide :
On donne la période sidérale de Jupiter, 4335,35 jours, bien connue à l'époque.
Solution :
En 261 jours, la Terre s'est déplacée d'un angle 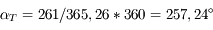
Jupiter s'est déplacée de 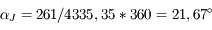
L'angle Jupiter-Soleil-Terre est donc à ce moment 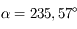
-
Question 6
Aide :
La distance Soleil-Jupiter est de 5,2 unités astronomiques.
Solution :
On considère le triangle JST. La loi des cosinus (ou théorème d'Al-Kashi) donne :
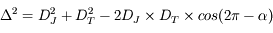
Soit 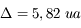
-
Question 7
Solution :
La différence de trajet est 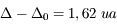
On a donc 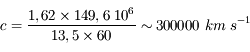
L'unité astronomique (distance Terre-Soleil) et la distance Jupiter-Soleil étaient les plus gros facteurs d'incertitude à l'époque. Römer semble avoir trouvé une valeur de 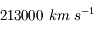 (soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
(soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
Cette étude peut être considérée comme le premier exemple historique d'effet Doppler-Fizeau, c'est-à-dire la variation de période apparente d'un phénomène régulier avec le déplacement de l'observateur.
pages_applications/exo-loi-aires-geo.html
Exercice
'La loi des aires'
pages_applications/exo-vit-orb-terre.html
Exercice
'Vitesse orbitale de la Terre'
-
Question 1
Solution :
La direction de l'étoile n'est pas contenue dans le plan de l'orbite de la Terre, il faut donc tenir compte de sa latitude écliptique 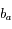 (angle entre la direction de l'étoile et le plan de l'écliptique).
(angle entre la direction de l'étoile et le plan de l'écliptique).
 Remarque
Remarque
Par rapport à la distance Terre-Soleil, l'étoile E est située à l'infini, donc la direction Terre-étoile TE est parallèle à la direction Soleil-étoile SE. Même chose pour les projections sur l'écliptique: Te est parallèle à Se.
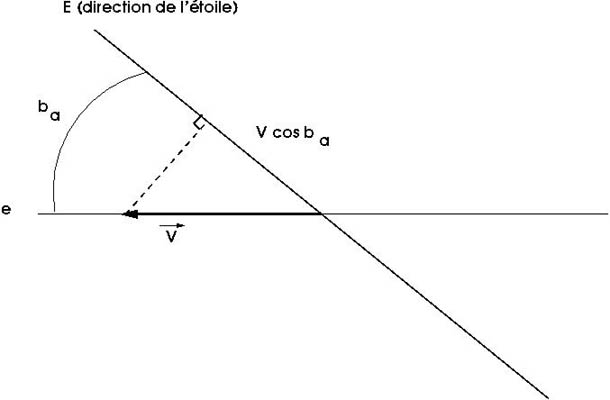
Direction de l'étoile et vitesse de la Terre à l'instant
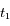
. Ainsi la vitesse radiale mesurée, due au seul mouvement de la Terre, a pour module
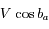
.
D'après la loi de composition des vitesses, on a:
Le choix des signes résulte de la constatation suivante:
-
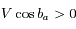
-
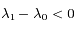 , donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant
, donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant 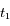 et
et 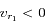
-
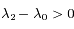 , donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant
, donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant 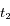 et
et 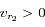
-
Question 2
Solution :
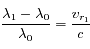
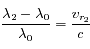
-
Question 3
Solution :
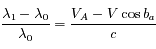 (1)
(1)
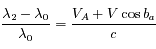 (2)
(2)
(1)+(2) ![\Longrightarrow V_A=\frac{c}{2 \lambda_0} [ (\lambda_1 - \lambda_0) + (\lambda_2 - \lambda_0) ]](../pages_applications/equations_applications/equation104.png)
(2)-(1) ![\Longrightarrow V=\frac{c}{2 \lambda_0 \cos b_a} [ (\lambda_2 - \lambda_0) - (\lambda_1 - \lambda_0) ]](../pages_applications/equations_applications/equation105.png)
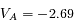 km.s
km.s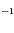
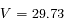 km.s
km.s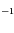
-
Question 4
Solution :
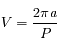
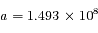 km.
km.
 Remarque
Remarque
- Au cours d'une année, la vitesse radiale due au mouvement de la Terre varie comme
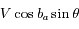 , où
, où 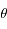 croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence
croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence 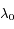 sera
sera 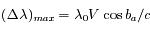 . Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer
. Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer 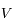 .
.
- La méthode utilisée ici n'est applicable que pour des étoiles dont la direction n'est pas perpendiculaire à l'écliptique (
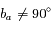 ). L'effet de décalage est d'autant plus important que
). L'effet de décalage est d'autant plus important que 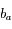 est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.
est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.
pages_applications/exo-equ-kepler-geo.html
Exercice
'Equation de Kepler'
pages_produits/exo-prod-2corps.html
Exercice
'La loi des aires'
pages_produits/exo-prod-2corps.html
Exercice
'Intégrale de Laplace'
pages_coniques/exo-balistique.html
Exercice
'Trajectoire balistique dans le système solaire'
-
Question 1
-
Question 2
-
Question 3
-
Question 4
-
Question 5
-
Question 6
Aide :
L'hyperbole des second foyers et une hyperbole-trajectoire (avant S)
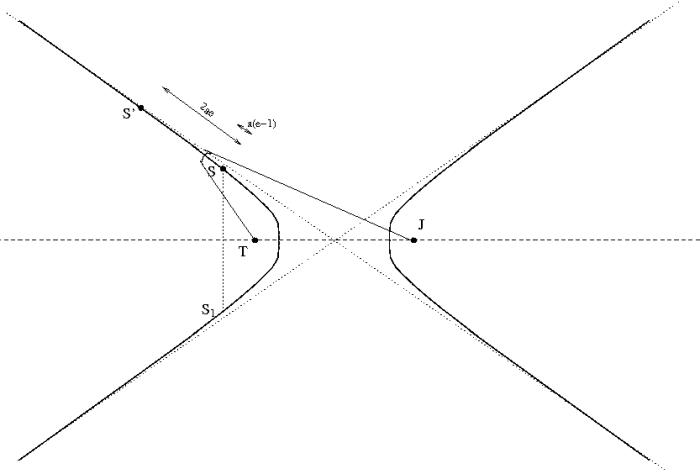
Aide :
L'hyperbole des second foyers et une hyperbole-trajectoire (avant S_1)
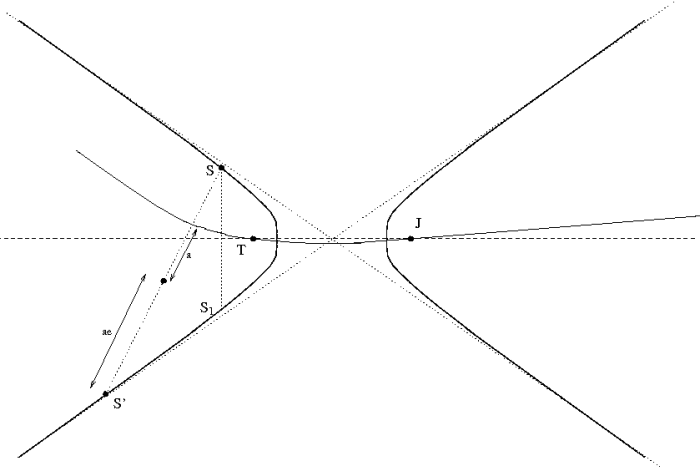
pages_coniques/exo-conique-pb-22-corps.html
Exercice
'Les solutions du problème de deux corps'
pages_coniques/exo-masse-trou-noir.html
Exercice
'Masse du trou noir central de la galaxie'
pages_geospace/exo-angles-solides.html
Exercice
'Angles solides'
-
Question 1
Solution :
Il ressort de la définition de la page précédente que 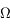 est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
On en déduit immédiatement qu'un demi-espace sous-tend un angle solide de 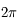 sr, et que l'espace complet sous-tend un angle solide de
sr, et que l'espace complet sous-tend un angle solide de 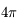 sr.
sr.
-
Question 2
Solution :
L'angle solide ne dépend que du contour sur lequel s'appuie la surface considérée, c'est-à-dire de la surface apparente. Dans la figure ci-dessous, les surfaces S et 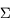 sont vues sous le même angle solide.
sont vues sous le même angle solide.
Une surface élémentaire dS se confond avec la calotte sphérique correspondante.
L'angle solide élémentaire est défini comme 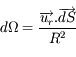 où
où 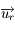 est le vecteur unitaire sur la ligne de visée, et
est le vecteur unitaire sur la ligne de visée, et 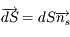 où
où 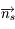 est le vecteur normal à la surface.
est le vecteur normal à la surface.
Si la surface dS est inclinée d'un angle 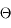 sur la ligne de visée, on a
sur la ligne de visée, on a 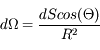
On notera que cette quantité est algébrique, ce qui permet de généraliser la première remarque à toutes les surfaces s'appuyant sur le même contour : les éléments qui "dépassent" du contour sont comptés positivement puis négativement.
-
Question 3
Solution :
A partir de l'expression de l'élément de surface, on trouve immédiatement :
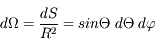
-
Question 4
Solution :
Puisqu'il y a symétrie de révolution, on intègre l'expression précédente le long de la couronne :
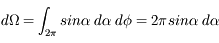
En intégrant ensuite l'angle 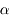 entre 0 et
entre 0 et 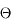 , on trouve l'angle solide défini par une calotte de demi-ouverture
, on trouve l'angle solide défini par une calotte de demi-ouverture 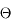 :
:
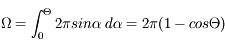
-
Question 5
Solution :
Pour les petites ouvertures, on a 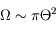 (où
(où 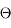 est donné en radians). Pour les très petits angles, on donne couramment les valeurs en
est donné en radians). Pour les très petits angles, on donne couramment les valeurs en 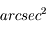 (secondes d'arc carrées) ou en
(secondes d'arc carrées) ou en 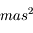 (milliarcsecondes carrées).
(milliarcsecondes carrées).
La taille apparente du Soleil et de la Lune vus depuis la Terre est d'environ 30' = 0,5°. L'angle solide correspondant est 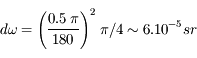
pages_geospace/exo-angles-solides.html
Exercice
'Photométrie'
-
Question 1
Solution :
La surface apparente de la source vue depuis le détecteur est 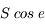 .
.
L'angle solide sous lequel le détecteur voit la source est donc 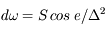
L'angle solide sous lequel la source voit le détecteur est 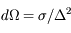
On a donc 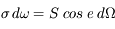
Cette quantité est appelée étendue de faisceau et joue un rôle important en optique instrumentale.
-
Question 2
Solution :
La puissance totale reçue par le détecteur est 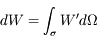
Soit par unité de surface 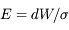
L'unité de mesure SI de l'éclairement est le 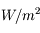 . Elle suppose une géométrie d'observation donnée (angle d'incidence sur le détecteur et distance à la source).
. Elle suppose une géométrie d'observation donnée (angle d'incidence sur le détecteur et distance à la source).
-
Question 3
Solution :
Avec les notations ci-dessus on a 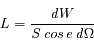
Dans le Système International, la luminance se mesure en 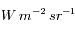 . Il s’agit d'une caractéristique intrinsèque à la source lumineuse, qui dépend a priori de la direction d'observation e.
. Il s’agit d'une caractéristique intrinsèque à la source lumineuse, qui dépend a priori de la direction d'observation e.
-
Question 4
Solution :
On a 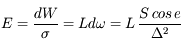
Si la source apparaît ponctuelle, la surface reste constante alors que la distance augmente. Le signal mesuré décroît en 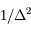 . C'est le cas des objets lointains non résolus, par exemple les étoiles observées au télescope.
. C'est le cas des objets lointains non résolus, par exemple les étoiles observées au télescope.
Si la source remplit le champ de l'instrument, l'angle solide sous lequel le détecteur voit la source ne dépend pas de la distance (plus on s'éloigne, plus la surface incluse dans le champ augmente) ; la relation entre E et L ne dépend donc que de l'incidence e et des propriétés angulaires de la luminance. C'est le cas des images satellitaires et de celles des sondes spatiales dans le Système solaire.
pages_geospace/exo-croissantlune.html
Exercice
-
Question 1
Solution :
Par la figure, on se rend compte que pour voir le croissant de Lune horizontal il est nécessaire et suffisant que le Soleil éclaire la Lune par au-dessous c'est à dire qu'ils aient le même azimut.
-
Question 2
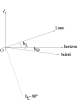
Solution :
Tout d'abord, il est préférable que le Soleil soit couché et donc
sa hauteur doit être négative. La Lune, quant à elle, doit être levée:
sa hauteur est donc positive.
Soit 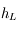 la hauteur de la Lune et
la hauteur de la Lune et 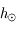 la hauteur du Soleil.
la hauteur du Soleil.
Si 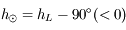 l'observateur voit exactement une demi-lune.
l'observateur voit exactement une demi-lune.
Ainsi pour avoir l'aspect indiqué sur la figure (un croissant comme
une gondole), il est nécessaire d'avoir 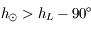 .
.
-
Question 3
-
Question 4
Aide :
Aucun calcul n'est nécessaire pour répondre à cette question. Une discussion avec les proprietés élémentaires de la géométrie sphérique devrait suffire.
Aide :
On sait qu'il n'y a qu'un seul grand cercle passant par deux points
de la sphère céleste. Or, la Lune et le Soleil sont sur un même grand
cercle (écliptique), et puisque 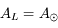 , les grands cercles
, les grands cercles
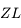 et
et 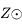 sont les mêmes. Ainsi le zénith
sont les mêmes. Ainsi le zénith 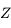 est sur l'écliptique.
est sur l'écliptique.
Aide :
"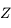 est sur l'écliptique"
est sur l'écliptique" 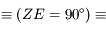 "
"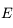 est sur l'horizon".
est sur l'horizon".
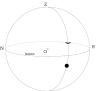
où 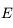 est le pôle de l'écliptique.
est le pôle de l'écliptique. 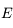 est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne.
est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne. 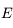 tourne autour du pôle céleste nord
tourne autour du pôle céleste nord 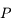 (fixe) à une même distance angulaire
(fixe) à une même distance angulaire 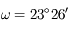 (obliquité) .
(obliquité) .
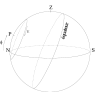
Solution :
La hauteur du pôle sur l'horizon correspond à la latitude du lieu (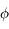 ).
).
On voit alors que pour une latitude comme celle de Lille (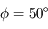 ),
cela est impossible. Ce n'est possible que si
),
cela est impossible. Ce n'est possible que si 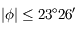 c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
 Calcul de la distance Terre-Lune
Calcul de la distance Terre-Lune Introduction
Introduction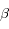 le demi-angle sous lequel ces deux astres sont vus depuis la Terre (voir partie droite de la figure ci-dessous). Cet angle est connu directement par l'observation et vaut à peu près 0,25°.
le demi-angle sous lequel ces deux astres sont vus depuis la Terre (voir partie droite de la figure ci-dessous). Cet angle est connu directement par l'observation et vaut à peu près 0,25°.
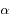 l'angle d'ouverture de ce cône. Sa valeur est a priori inconnue. Aristarque de Samos avait observé que la largeur de ce cône au niveau de la Lune était de 3 diamètres lunaires.
l'angle d'ouverture de ce cône. Sa valeur est a priori inconnue. Aristarque de Samos avait observé que la largeur de ce cône au niveau de la Lune était de 3 diamètres lunaires.

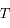 ,
, 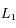 ,
, 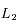 et
et 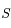 sont respectivement les positions de la Terre, de la Lune pendant une éclipse de soleil, de la Lune pendant une éclipse de Lune, et du Soleil.
sont respectivement les positions de la Terre, de la Lune pendant une éclipse de soleil, de la Lune pendant une éclipse de Lune, et du Soleil. 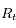
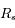 et
et 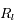 sont les rayons terrestre, solaire et lunaire.
sont les rayons terrestre, solaire et lunaire.
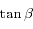 et
et 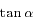 en fonction de
en fonction de 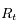
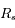 et
et 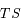 .
.
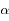 et
et 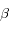 si on suppose le Soleil très grand devant la Terre ?
si on suppose le Soleil très grand devant la Terre ?
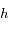 (défini sur la figure).
(défini sur la figure).
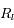 et
et 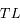 en fonction de
en fonction de 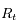 .
.
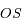 en fonction de
en fonction de 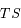 ,
, 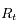 et
et 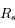 .
.
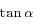 quand
quand 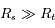
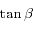 en fonction de
en fonction de 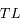 et
et 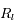 .
.
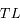 et de hauteur
et de hauteur 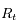 est un rectangle.
est un rectangle.
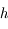 , sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
, sur quelle partie de la Terre (supposée sphérique) est visible le satellite?
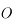 (centre de la Terre),
(centre de la Terre), 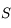 (satellite) et
(satellite) et 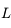 (un lieu de la Terre où
(un lieu de la Terre où 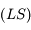 est tangent à
la Terre. On note
est tangent à
la Terre. On note 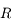 le rayon de la Terre.
le rayon de la Terre.
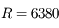 km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
km, à quelle distance maximale du point de la Terre survolé par le satellite peut-on voir le satellite d'altitude
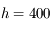 km?
km?
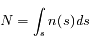
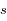 est la coordonnée le long du trajet du rayon et
est la coordonnée le long du trajet du rayon et 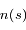 est la densité atmosphérique au point de coordonnée
est la densité atmosphérique au point de coordonnée 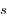 .
.
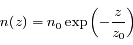
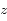 est l'altitude (mesurée verticalement),
est l'altitude (mesurée verticalement), 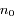 est la densité au niveau du sol, et
est la densité au niveau du sol, et 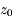 est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la
est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la 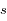 sur le trajet du rayon de Soleil, et d'altitude
sur le trajet du rayon de Soleil, et d'altitude 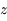 .
. 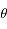 est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.

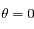 ), donner l'expression de l'altitude
), donner l'expression de l'altitude 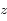 en fonction de la coordonnée
en fonction de la coordonnée 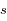 .
.
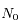 , la densité de colonne au Soleil couchant (
, la densité de colonne au Soleil couchant (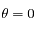 ). On remarque que la densité de particules décroît rapidement avec l'altitude et devient petite pour
). On remarque que la densité de particules décroît rapidement avec l'altitude et devient petite pour 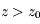 ; on peut donc tronquer l'intégrale à une altitude maximum telle que
; on peut donc tronquer l'intégrale à une altitude maximum telle que 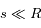 (l'atmosphère est fine par rapport à la taille de la planète).
(l'atmosphère est fine par rapport à la taille de la planète).
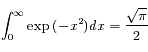
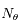 , la densité de colonne pour une position
, la densité de colonne pour une position 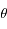 quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc
quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc 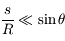 .
.
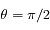 . Calculer le rapport
. Calculer le rapport 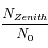 . Pour l'application numérique on prendra
. Pour l'application numérique on prendra 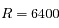 km,
km, 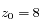 km (échelle de hauteur de l'atmosphère terrestre).
km (échelle de hauteur de l'atmosphère terrestre).
 de l'exercice précédent est appelé
de l'exercice précédent est appelé 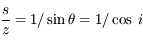 , où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'
, où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'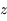 et la coordonnée
et la coordonnée 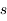 pour une hauteur
pour une hauteur 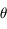 quelconque.
quelconque.
 (compté à partir de la verticale locale).
(compté à partir de la verticale locale).
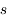 .
.
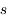 en fonction de l'angle zénital
en fonction de l'angle zénital  et comparer avec l'approximation usuelle en sécante (
et comparer avec l'approximation usuelle en sécante (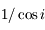 ).
).

 en unités astronomiques au moment de la deuxième observation.
en unités astronomiques au moment de la deuxième observation.

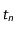 de durée très courte
de durée très courte 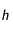 de telle sorte que
de telle sorte que 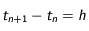 . La discrétisation revient à supposer qu'entre les instants
. La discrétisation revient à supposer qu'entre les instants 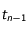 et
et 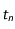 , le mobile se déplace de
, le mobile se déplace de 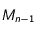 à
à 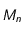 avec la vistesse constante
avec la vistesse constante 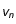 . En vecteur la vistesse est donc
. En vecteur la vistesse est donc 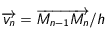 . Sur l'intervalle suivant
. Sur l'intervalle suivant ![[t_n,t_{n+1}]](../pages_applications/equations_applications/equation10.png) , la vitesse est différente mais constante aussi pour cette durée:
, la vitesse est différente mais constante aussi pour cette durée: 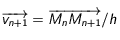 . Ainsi à l'instant
. Ainsi à l'instant 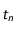 l'accélération est
l'accélération est 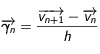 .
.
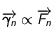
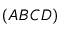 un parallélogramme. La diagonale
un parallélogramme. La diagonale ![[AC]](../pages_applications/equations_applications/equation16.png) partage le parallélogramme en deux triangles de même aire:
partage le parallélogramme en deux triangles de même aire: 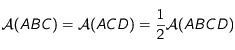 . Plus généralement, pout tout point
. Plus généralement, pout tout point 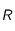 de
de ![[CD]](../pages_applications/equations_applications/equation19.png) , on a :
, on a : 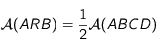 .
.
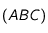 un triangle et
un triangle et 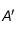 le milieu de
le milieu de ![[BC]](../pages_applications/equations_applications/equation23.png) . La médiane
. La médiane ![[AA']](../pages_applications/equations_applications/equation24.png) partage le triangle en deux triangles de même aire:
partage le triangle en deux triangles de même aire: 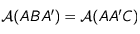 .
.
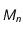 est soumis à une force centrale, c'est-à-dire dirigée vers un point
est soumis à une force centrale, c'est-à-dire dirigée vers un point 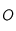 fixe (le Soleil par exemple si la masse de
fixe (le Soleil par exemple si la masse de 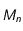 est négligeable par rapport à celle du Soleil): la force est
est négligeable par rapport à celle du Soleil): la force est 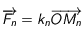 .
.
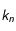 même si on sait que pour la loi de Newton ce scalaire est négatif et inversement proportionnel au carré de la distance
même si on sait que pour la loi de Newton ce scalaire est négatif et inversement proportionnel au carré de la distance 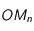
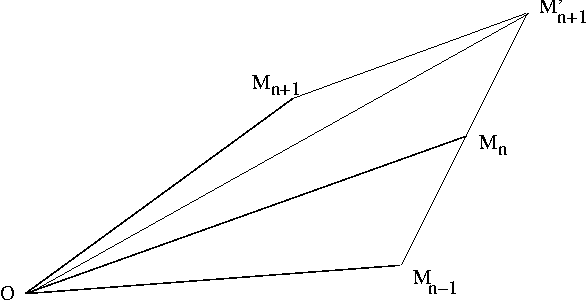
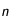 ), on a:
), on a: 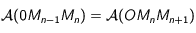
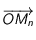 est proportionnel au temps parcouru.
est proportionnel au temps parcouru.
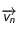 et
et 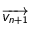 (vitesses du mobile aux temps
(vitesses du mobile aux temps 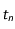 et
et 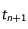 ) et considérer le point
) et considérer le point 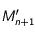 qu'occuperait le mobile au temps
qu'occuperait le mobile au temps 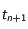 si le mouvement était uniforme.
si le mouvement était uniforme.
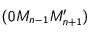 pour avoir
pour avoir 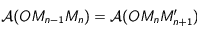
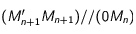 , puis prendre
, puis prendre 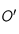 de telle manière que
de telle manière que 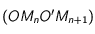 soit un parallélogramme et enfin lui appliquer le lemme correspondant avec
soit un parallélogramme et enfin lui appliquer le lemme correspondant avec 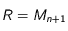 puis avec
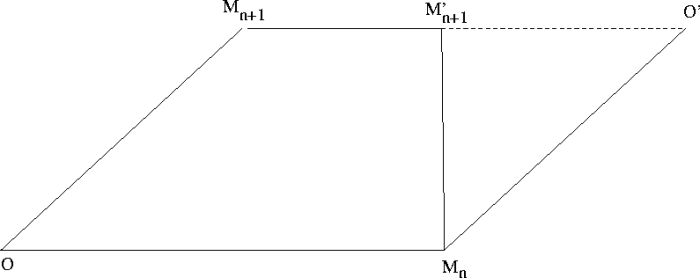
puis avec 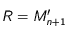 .
.
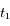 et
et 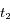 espacées de 6 mois.
espacées de 6 mois.
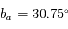 , et la longitude par rapport à une direction fixe
, et la longitude par rapport à une direction fixe 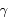 est
est 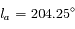 . A l'instant
. A l'instant 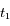 la longitude de la Terre est
la longitude de la Terre est 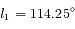 , et
, et 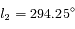 à l'instant
à l'instant 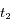 . Voir la figure ci-dessous pour les conditions d'observation.
. Voir la figure ci-dessous pour les conditions d'observation.

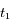 et
et 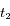 un
un 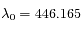 nm, est mesurée
nm, est mesurée 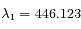 nm sur le spectre obtenu à la date
nm sur le spectre obtenu à la date 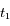 , et
, et 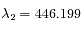 nm sur celui obtenu à la date
nm sur celui obtenu à la date 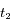 .
.
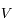 .
.
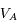 la
la 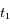 et
et 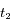 ). Ecrire en fonction de
). Ecrire en fonction de 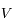 ,
, 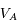 et
et 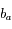 la vitesse radiale d'Arcturus par rapport à l'observateur à l'instant
la vitesse radiale d'Arcturus par rapport à l'observateur à l'instant 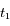 (on notera cette vitesse
(on notera cette vitesse 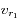 ), ainsi qu'à l'instant
), ainsi qu'à l'instant 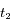 (notée
(notée 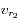 ).
).
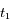 et
et 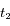 pour la longueur d'onde de référence
pour la longueur d'onde de référence 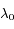 , écrire les expressions de
, écrire les expressions de 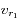 et
et 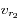 .
.
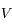 et
et 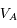 en fonction des longueurs d'onde
en fonction des longueurs d'onde 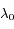 ,
, 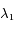 et
et 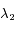 . Calculer leur valeur numériquement en km.s
. Calculer leur valeur numériquement en km.s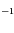 .
.
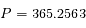 jours.
jours.
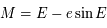 ) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne
) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne 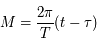 , avec
, avec 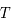 la période orbitale,
la période orbitale,  le temps et
le temps et 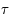 l'instant de passage au péricentre.
l'instant de passage au péricentre.


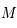 (de foyer
(de foyer 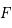 , péricentre
, péricentre 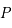 , demi-grand axe
, demi-grand axe 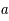 , excentricité
, excentricité 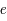 ), cercle principal, anomalie excentrique
), cercle principal, anomalie excentrique 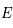 et vraie
et vraie 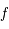
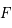 ,
, 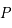 ,
, 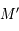 en fonction de
en fonction de 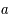 ,
, 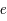 ,
, 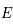 .
.
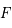 ,
, 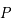 ,
, 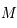 .
.
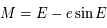 .
.
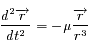
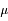 est une constante réelle positive et
est une constante réelle positive et 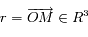 .
. 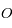 est un point fixe et on étudie le mouvement de
est un point fixe et on étudie le mouvement de 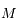 .
.

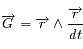
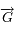 et utiliser que
et utiliser que 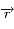 et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
et sa dérivée seconde sont colinéaires (ce qui indique que la loi des aires est vrai pour toute force centrale).
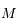 se fait dans un plan passant par le point
se fait dans un plan passant par le point 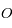 et orthogonal à
et orthogonal à 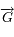 .
.
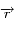 et
et 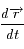 sont toujours (quelque soit le temps) orthogonaux à
sont toujours (quelque soit le temps) orthogonaux à 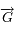 , avec l'hypothèse toutefois que
, avec l'hypothèse toutefois que 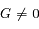 .
.
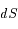 parcouru par
parcouru par 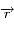 pendant l'élément de temps
pendant l'élément de temps 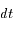 , montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
, montrer la loi des aires proprement dite: L'aire balayée par unité de temps est constante.
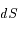 est la moitié du parallélogramme suivant:
est la moitié du parallélogramme suivant:
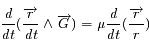
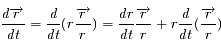
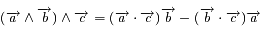
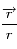 est constante donc
est constante donc 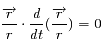
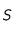 . Sous cette hypothèse, le mouvement de cette sonde autour du Soleil est un mouvement képlérien c'est-à-dire que la trajectoire est une
. Sous cette hypothèse, le mouvement de cette sonde autour du Soleil est un mouvement képlérien c'est-à-dire que la trajectoire est une 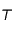 et
et 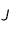 du système solaire avec
du système solaire avec 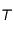 plus près de
plus près de 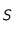 que
que 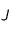 . On peut considérer que
. On peut considérer que 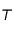 est la Terre et que
est la Terre et que 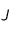 est Jupiter. Cela permet de fixer les idées mais il n'y a aucune obligation formelle à cela. On fait partir la sonde du point
est Jupiter. Cela permet de fixer les idées mais il n'y a aucune obligation formelle à cela. On fait partir la sonde du point 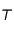 pour qu'elle arrive au point
pour qu'elle arrive au point 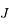 .
. 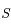 étant l'un des foyers, on note
étant l'un des foyers, on note 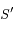 le second foyer de la conique
le second foyer de la conique 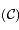 qui définit la trajectoire.
qui définit la trajectoire.

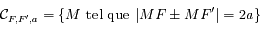 . Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
. Préciser le cas d'une ellipse et le cas d'une hyperbole. Pour ce dernier cas, préciser aussi comment sont distinguées les deux branches de l'hyperbole.
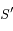 se trouve sur une hyperbole
se trouve sur une hyperbole 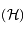 de foyers
de foyers 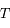 et
et 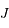 passant par
passant par 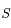
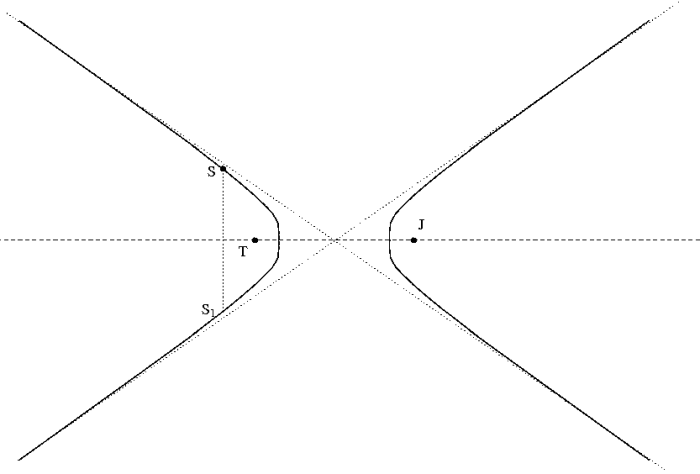
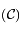 suivant la branche de
suivant la branche de 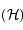 sur laquelle se trouve
sur laquelle se trouve 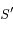 .
.
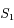 le point de
le point de 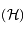 symétrique de
symétrique de 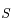 par rapport à l'axe focal.
par rapport à l'axe focal.
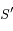 se trouve entre
se trouve entre 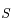 et
et 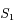 .
.
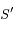 sur
sur 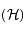 , exprimer le demi-grand axe
, exprimer le demi-grand axe 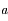 et l'
et l' de la conique
de la conique 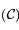 en fonction des distances entre les points
en fonction des distances entre les points 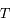 ,
, 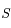 et
et 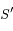
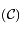 quand
quand
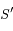 tend vers
tend vers 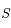
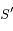 tend vers
tend vers 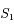
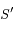 tend vers l'infini sur la même branche
tend vers l'infini sur la même branche

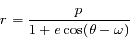
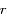 est la distance entre un corps
est la distance entre un corps 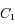 se trouvant à l'origine et le second corps
se trouvant à l'origine et le second corps 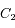 , et
, et 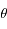 l'angle entre une direction de référence et le vecteur
l'angle entre une direction de référence et le vecteur 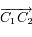 et
et  un nombre réel supérieur ou égale à zéro et
un nombre réel supérieur ou égale à zéro et 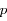 un nombre réel strictement supérieur à zéro.
un nombre réel strictement supérieur à zéro.
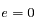 la solution est un cercle dont on déterminera le rayon.
la solution est un cercle dont on déterminera le rayon.
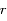 que l'on déterminera et que l'on notera
que l'on déterminera et que l'on notera 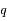 . La position pour laquelle cette distance est atteinte s'appelle le péricentre.
A quoi correspond
. La position pour laquelle cette distance est atteinte s'appelle le péricentre.
A quoi correspond 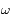 ?
Quand est-il pour le maximum de
?
Quand est-il pour le maximum de 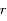 ? La position pour laquelle cette distance, notée
? La position pour laquelle cette distance, notée 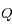 , est atteinte s'appelle apocentre lorsqu'elle existe.
, est atteinte s'appelle apocentre lorsqu'elle existe.
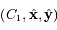 où l'axe des abscisses
où l'axe des abscisses 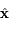 est dirigé vers le pericentre. Pour un point
est dirigé vers le pericentre. Pour un point 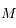 du plan on note
du plan on note 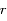 la distance
la distance 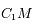 et
et 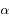 l'angle entre l'axe des abscisses et le vecteur
l'angle entre l'axe des abscisses et le vecteur 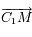 .
Ecrire l'équation de la
.
Ecrire l'équation de la 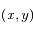 de
de 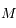 dans le repère
dans le repère 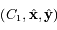 .On remarquera que l'équation obtenue est léquation générale d'une conique.
.On remarquera que l'équation obtenue est léquation générale d'une conique.
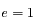 on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
on obtient l'équation d'une parabole dont on déterminera les coordonnées du péricentre.
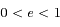 on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
on obtient l'équation d'une ellipse dont on déterminera le centre, le demi-grand axe et le demi-petit axe.
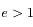 on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.
on obtient l'équation d'une hyperbole dont on déterminera le péricentre et les asymptotes.

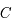 de l'ellipse projetée
de l'ellipse projetée
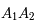
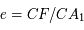 , puis
, puis 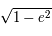 .
.
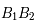 de
de 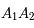 (donc le projeté du petit axe).
(donc le projeté du petit axe).
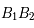 et de rapport
et de rapport 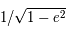 .
.
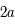 du grand axe de l'orbite réelle.
du grand axe de l'orbite réelle.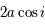 où
où 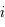 est l'inclinaison du plan de l'orbite avec le plan de projection.
est l'inclinaison du plan de l'orbite avec le plan de projection.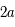 sur ce grand axe, puis convertir cette valeur en UA (
sur ce grand axe, puis convertir cette valeur en UA (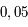 seconde de degré) et la distance du Soleil au centre de la Galaxie (26 000
seconde de degré) et la distance du Soleil au centre de la Galaxie (26 000 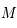 présente au foyer SgrA.
présente au foyer SgrA.
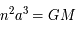 où
où 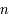 est la vitesse angulaire (
est la vitesse angulaire (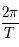 ), a le demi grand axe, M la masse et G une constante universelle (la constante de Gravitation).
), a le demi grand axe, M la masse et G une constante universelle (la constante de Gravitation).
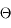 . On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
. On considère la calotte sphérique de rayon R et d'aire S(R) délimitée par ce cône. La quantité
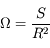

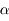 . Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture
. Donner l'expression de l'angle solide en fonction de cet angle. En déduire l'angle solide sous-tendu par une calotte de demi-ouverture 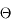 .
.
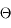 est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
est petit ? Estimer l'angle solide sous lequel on voit le Soleil et la Lune depuis la Terre.
 , on observe la source de surface S sous un angle e à la distance
, on observe la source de surface S sous un angle e à la distance  . Les dimensions sont telles que les angles solides considérés sont petits (
. Les dimensions sont telles que les angles solides considérés sont petits (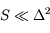 ).
).


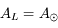 , les grands cercles
, les grands cercles
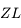 et
et 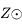 sont les mêmes. Ainsi le zénith
sont les mêmes. Ainsi le zénith 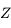 est sur l'écliptique.
est sur l'écliptique.
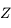 est sur l'écliptique"
est sur l'écliptique" 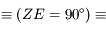 "
"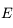 est sur l'horizon".
est sur l'horizon".
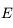 est le pôle de l'
est le pôle de l'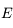 est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne.
est un point de la sphère
des fixes (c'est à dire, lié aus étoiles). A ce titre, et comme toutes les étoiles, il est affecté
par le mouvement diurne. 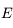 tourne autour du pôle céleste nord
tourne autour du pôle céleste nord 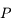 (fixe) à une même distance angulaire
(fixe) à une même distance angulaire 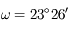 (obliquité) .
(obliquité) .
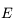 de l'écliptique) sur la sphère locale (de pôle
de l'écliptique) sur la sphère locale (de pôle 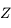 ).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de
).
Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de 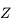 sur la sphère des fixes. On utilise la
condition suivante:
sur la sphère des fixes. On utilise la
condition suivante:
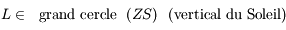

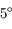 au plus (en bas).
au plus (en bas).
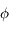 donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des
donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des 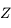 ). A chacune de
ces positions de
). A chacune de
ces positions de 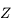 , il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des
, il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des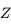 . En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des
. En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des 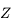 est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
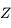 .
.
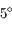 sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de
sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de 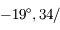 an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de
an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de 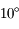 . Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
. Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
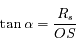
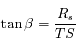
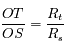 or
or 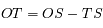 . On a donc
. On a donc 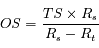 et
et 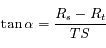
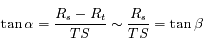
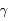 et
et 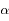 sont alternes-internes et donc égaux.
sont alternes-internes et donc égaux.
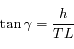 . Par ailleurs,
. Par ailleurs, 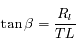 et
et 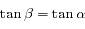 d'après la question précédente.
d'après la question précédente.
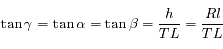
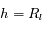
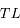 et de hauteur
et de hauteur 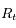 . Le côté opposé à
. Le côté opposé à 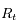 est de longueur
est de longueur 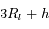 d'après les observations d'Aristarque de Samos. Et d'après nos calculs précédents
d'après les observations d'Aristarque de Samos. Et d'après nos calculs précédents 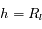 . En égalisant les deux hauteurs du rectangle on obtient donc
. En égalisant les deux hauteurs du rectangle on obtient donc 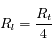 .
.
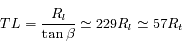
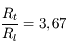 et
et 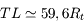
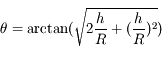 . On peut écrire aussi
. On peut écrire aussi
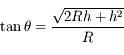
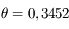 radians. La distance maximale est
radians. La distance maximale est 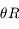 , soit
, soit 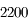 km.
km.
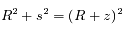
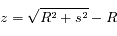
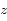 au premier ordre :
au premier ordre :
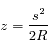
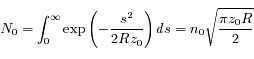
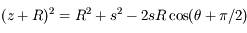
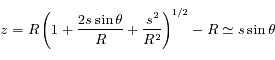
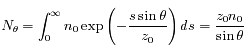
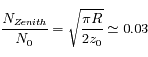
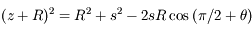
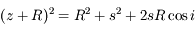
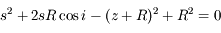
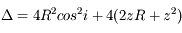
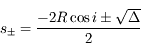
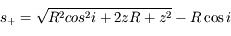

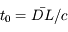 , le second avec
, le second avec 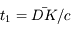 . L'intervalle entre les observations est donc
. L'intervalle entre les observations est donc 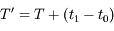 . Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et
. Attention, en général les points D, L et K ne sont pas alignés comme sur la figure, et 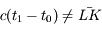 .
.
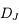 la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors
la distance Soleil-Jupiter mesurée en unités astronomiques, supposée constante. La distance Terre-Jupiter à l'opposition est alors 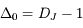 ua.
ua.
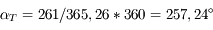
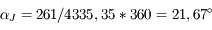
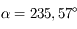
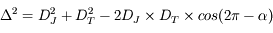
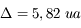
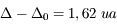
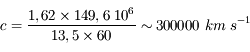
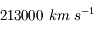 (soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
(soit une erreur de 30%, mais un ordre de grandeur correct), et pensait surtout avoir démontré que la lumière se propage à vitesse finie.
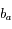 (angle entre la direction de l'étoile et le plan de l'écliptique).
(angle entre la direction de l'étoile et le plan de l'écliptique).

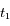 . Ainsi la vitesse radiale mesurée, due au seul mouvement de la Terre, a pour module
. Ainsi la vitesse radiale mesurée, due au seul mouvement de la Terre, a pour module 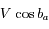 .
.
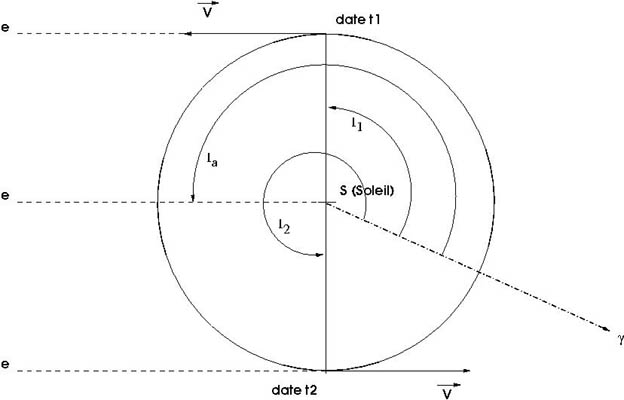
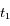 ,
, 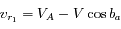
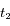 ,
, 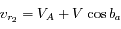
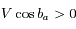
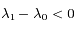 , donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant
, donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant 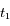 et
et 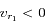
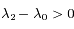 , donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant
, donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant 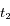 et
et 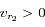
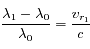
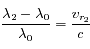
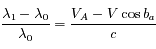 (1)
(1)
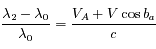 (2)
(2)
![\Longrightarrow V_A=\frac{c}{2 \lambda_0} [ (\lambda_1 - \lambda_0) + (\lambda_2 - \lambda_0) ]](../pages_applications/equations_applications/equation104.png)
![\Longrightarrow V=\frac{c}{2 \lambda_0 \cos b_a} [ (\lambda_2 - \lambda_0) - (\lambda_1 - \lambda_0) ]](../pages_applications/equations_applications/equation105.png)
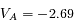 km.s
km.s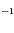
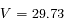 km.s
km.s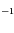
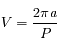
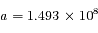 km.
km.
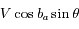 , où
, où 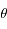 croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence
croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence 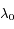 sera
sera 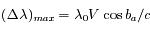 . Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer
. Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer 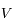 .
.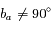 ). L'effet de décalage est d'autant plus important que
). L'effet de décalage est d'autant plus important que 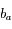 est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.
est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.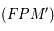 = aire
= aire 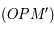 - aire
- aire 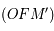
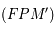 =
= 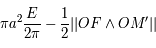
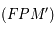 =
= 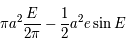
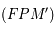 =
= 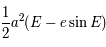
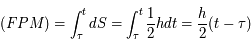
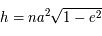 , où
, où 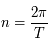 est le moyen mouvement.
est le moyen mouvement.
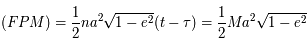 .
.
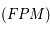 =
=  aire
aire 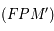 =
= 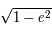 aire
aire 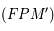 , où
, où 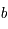 est le demi-petit axe de l'ellipse.
est le demi-petit axe de l'ellipse.
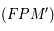 =
= 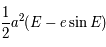 et aire
et aire 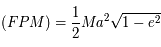 . On obtient donc
. On obtient donc 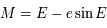 .
.
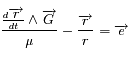
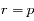 ce qui est bien l'équation d'un cercle de centre
ce qui est bien l'équation d'un cercle de centre 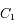 et de rayon
et de rayon 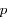 .
.
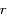 sera minimal quand
sera minimal quand 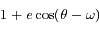 sera maximal, c'est à dire lorsque
sera maximal, c'est à dire lorsque ![\theta=\omega \,\,\,{\rm mod}\,[2\pi]](../pages_coniques/equations_coniques/equation62.png) . Dans ce cas on a
. Dans ce cas on a 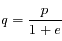 .
.
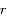 sera maximal quand
sera maximal quand 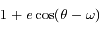 sera minimal, c'est-à-dire lorsque
sera minimal, c'est-à-dire lorsque ![\theta=\omega+\pi \,\,\,{\rm mod}\,[2\pi]](../pages_coniques/equations_coniques/equation66.png) . Or si
. Or si 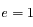 on s'aperçoit que dans ce cas
on s'aperçoit que dans ce cas 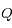 n'est pas défini, et si
n'est pas défini, et si 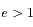 alors
alors 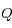 est négatif ce qui n'a pas de sens.
Lorsqu'il est défini (
est négatif ce qui n'a pas de sens.
Lorsqu'il est défini (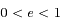 ), on a
), on a 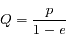 . On remarque que l'apocentre se trouve à l'opposé du péricentre.
. On remarque que l'apocentre se trouve à l'opposé du péricentre.
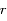 et
et 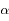 l'équation devient :
l'équation devient :
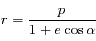 .
Avec
.
Avec 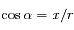 on a:
on a:
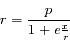 qui se transforme facilement en
qui se transforme facilement en 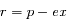 . On obtient finalement
. On obtient finalement
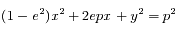 qui est l'équation d'une conique.
qui est l'équation d'une conique.
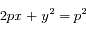 ,
,
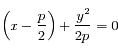 .
.
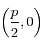 .
.
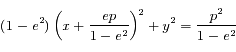 qui devient :
qui devient :
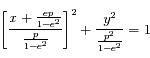
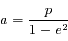 et
et 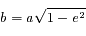 (qui est défini puisque
(qui est défini puisque 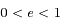 ), l'équation
devient:
), l'équation
devient:
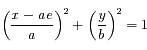
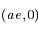 , de demi-grand axe
, de demi-grand axe 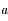 et de demi-petit axe
et de demi-petit axe 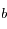 .
.
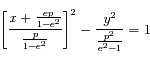
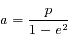 et
et 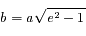 (qui est défini puisque cette fois
(qui est défini puisque cette fois 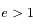 ). Ainsi l'équation devient:
). Ainsi l'équation devient:
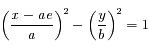
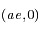 , et d'asymptotes :
, et d'asymptotes :
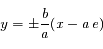 .
.
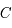 et par l'image du foyer
et par l'image du foyer 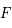 (c'est à dire la position indiquée de SgrA).
(c'est à dire la position indiquée de SgrA).
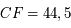 mm et
mm et 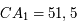 mm
mm
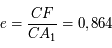
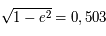 .
.
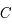 au milieu d'une corde parallèle à
au milieu d'une corde parallèle à 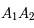 .
.
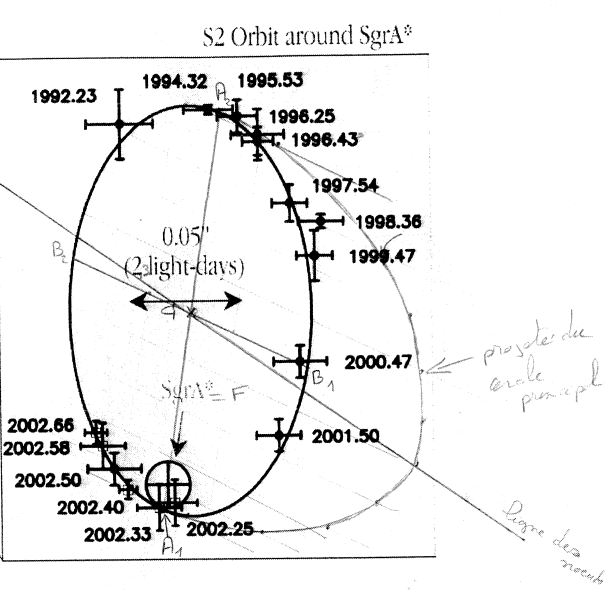
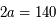 mm ce qui correspond à
mm ce qui correspond à 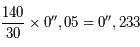
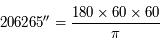 . Ce qui donne
. Ce qui donne 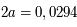 al
al 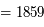 ua.
ua.
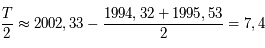 ans. Donc
ans. Donc 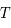 est estimée à
est estimée à 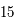 ans.
ans.
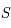 correspond au Soleil.
correspond au Soleil.
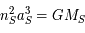 et
et 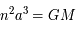 d'où
d'où 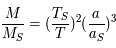
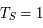 an et
an et 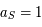 ua, donc
ua, donc 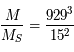 . Et donc
. Et donc 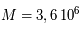 masses solaires.
masses solaires.
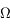 est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
est aussi égal à l'aire de la calotte découpée par le cône sur la sphère de centre O et de rayon unité.
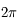 sr, et que l'espace complet sous-tend un angle solide de
sr, et que l'espace complet sous-tend un angle solide de 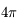 sr.
sr.
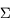 sont vues sous le même angle solide.
sont vues sous le même angle solide.
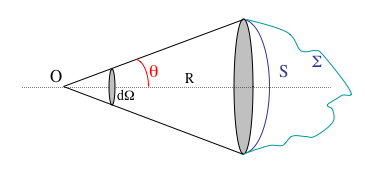
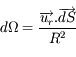 où
où 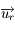 est le vecteur unitaire sur la ligne de visée, et
est le vecteur unitaire sur la ligne de visée, et 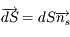 où
où 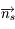 est le vecteur normal à la surface.
est le vecteur normal à la surface.
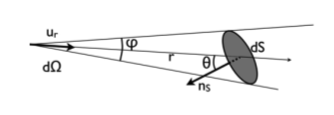
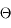 sur la ligne de visée, on a
sur la ligne de visée, on a 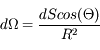
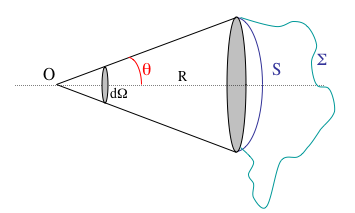
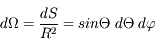
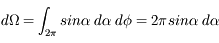
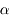 entre 0 et
entre 0 et 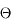 , on trouve l'angle solide défini par une calotte de demi-ouverture
, on trouve l'angle solide défini par une calotte de demi-ouverture 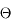 :
:
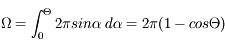
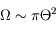 (où
(où 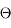 est donné en radians). Pour les très petits angles, on donne couramment les valeurs en
est donné en radians). Pour les très petits angles, on donne couramment les valeurs en 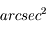 (secondes d'arc carrées) ou en
(secondes d'arc carrées) ou en 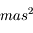 (milliarcsecondes carrées).
(milliarcsecondes carrées).
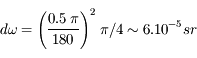
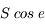 .
.
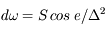
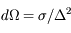
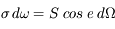
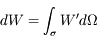
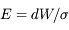
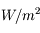 . Elle suppose une géométrie d'observation donnée (angle d'incidence sur le détecteur et distance à la source).
. Elle suppose une géométrie d'observation donnée (angle d'incidence sur le détecteur et distance à la source).
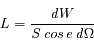
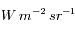 . Il s’agit d'une caractéristique intrinsèque à la source lumineuse, qui dépend a priori de la direction d'observation e.
. Il s’agit d'une caractéristique intrinsèque à la source lumineuse, qui dépend a priori de la direction d'observation e.
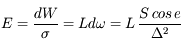
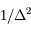 . C'est le cas des objets lointains non résolus, par exemple les étoiles observées au télescope.
. C'est le cas des objets lointains non résolus, par exemple les étoiles observées au télescope.
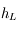 la hauteur de la Lune et
la hauteur de la Lune et 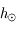 la hauteur du Soleil.
la hauteur du Soleil.
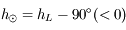 l'observateur voit exactement une demi-lune.
l'observateur voit exactement une demi-lune.
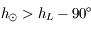 .
.
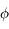 ).
).
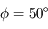 ),
cela est impossible. Ce n'est possible que si
),
cela est impossible. Ce n'est possible que si 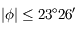 c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.