Auteur: Alain Vienne

 Exercice
Exercice
Difficulté : ☆☆
Temps : 2h
Question 1)
Montrer que la condition d'horizontalité du croissant de Lune nécessite que la Lune et le Soleil aient le même azimut.
Solution
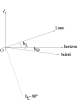
Par la figure, on se rend compte que pour voir le croissant de Lune horizontal il est nécessaire et suffisant que le Soleil éclaire la Lune par au-dessous c'est à dire qu'ils aient le même azimut.
Question 2)
La condition de même azimut est donc une condition nécessaire. Réciproquement, si cette condition est réalisée, préciser les conditions sur les hauteurs du Soleil et de la Lune pour que le croissant soit vu comme une "gondole" et non à l'envers (un "D" renversé).
La hauteur est l'angle sur le vertical (cercle de même azimut). Il est compté de -90° à 90° par rapport à l'horizon.
Solution
Tout d'abord, il est préférable que le Soleil soit couché et donc
sa hauteur doit être négative. La Lune, quant à elle, doit être levée:
sa hauteur est donc positive.
Soit 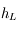 la hauteur de la Lune et
la hauteur de la Lune et 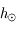 la hauteur du Soleil.
la hauteur du Soleil.
Si 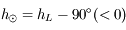 l'observateur voit exactement une demi-lune.
l'observateur voit exactement une demi-lune.
Ainsi pour avoir l'aspect indiqué sur la figure (un croissant comme
une gondole), il est nécessaire d'avoir 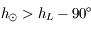 .
.
Question 3)
Cette figure donne, pour chaque position
de la Lune sur le même vertical que le Soleil (quand la condition
est réalisée), l'aspect de celle-ci.
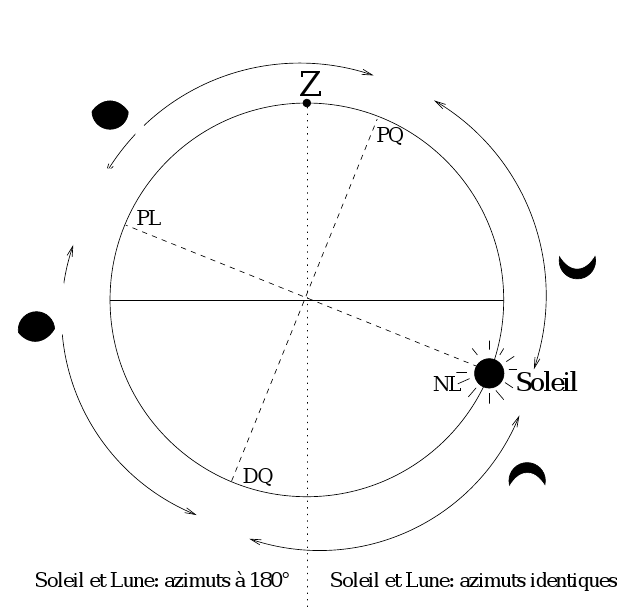
Phases de la Lune sous la condition de
même azimut. Figure dans le vertical de la Lune (et du Soleil).
La position du zénith sur le cercle est indicatif. Elle correspond
au cas de la figure donnée en solution de la question précédente. Bien-sur, si le zénith
est ailleurs sur le cercle, cela change les conditions de lever/coucher
du Soleil et de la Lune. Faites d'autres figures en changeant le zénith de place (cela déplace aussi l'horizon).
Question 4)
En supposant que la Lune est toujours sur l'écliptique, donner les seuls endroits de la Terre où il est possible de voir le croissant de Lune horizontal.
AideAideAideSolution
Aucun calcul n'est nécessaire pour répondre à cette question. Une discussion avec les proprietés élémentaires de la géométrie sphérique devrait suffire.
La hauteur du pôle sur l'horizon correspond à la latitude du lieu (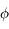 ).
).
On voit alors que pour une latitude comme celle de Lille (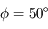 ),
cela est impossible. Ce n'est possible que si
),
cela est impossible. Ce n'est possible que si 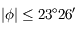 c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.
c'est à dire, entre les tropiques. En ces lieux, la condition est
réalisée 2 fois par jour.


